Collisions of Point Masses in Two Dimensions

Saul Beceiro-Novo

Linear Momentum and Collisions

57 Collisions of Point Masses in Two Dimensions

Learning Objectives

Discuss two-dimensional collisions as an extension of one-dimensional analysis.
Define point masses.
Derive an expression for conservation of momentum along the x– and y-axes.
Describe elastic collisions of two objects with equal mass.
Determine the magnitude and direction of final velocity given initial velocity and scattering angle.

In earlier sections, we studied collisions where all motion occurred along a single line (one dimension). However, many collisions in the real world—such as interactions between molecules, cells, or even two people in sports—occur in two dimensions. A classic example is two billiard balls scattering after impact. To analyze these more complex interactions, we extend our one-dimensional framework to two dimensions using components of motion along perpendicular axes (usually [latex]x[/latex] and [latex]y[/latex]).

As in previous cases, if the net external force is zero, total momentum is conserved. Even in two-dimensional collisions, this fundamental principle holds true. We simplify the analysis by choosing a coordinate system aligned with the direction of motion of one of the particles, especially when one particle is initially at rest. This setup is common in lab experiments and medical technologies like radiation therapy, where beams interact with particles at rest in tissue.

To avoid complications such as spinning or rotation, we begin by modeling objects as point masses—idealized particles with no internal structure. Rotation will be discussed later in the course.

Consider a particle of mass [latex]m_1[/latex] moving toward another particle of mass [latex]m_2[/latex] that is initially at rest. We align the coordinate system so that [latex]m_1[/latex] travels along the [latex]x[/latex]-axis. After the collision, both particles move off at angles [latex]\theta_1[/latex] and [latex]\theta_2[/latex], as shown in Figure 57.1.. Momentum conservation applies separately in both the [latex]x[/latex]– and [latex]y[/latex]-directions.

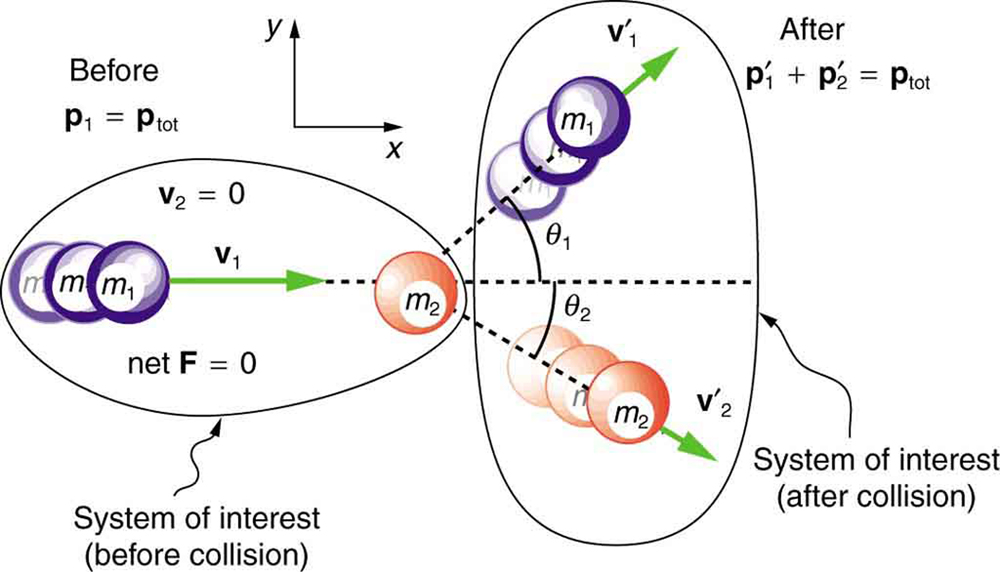
A purple ball of mass m1 moves with velocity V 1 toward the right side along the X direction. The orange ball of mass m 2 is initially at rest. The total momentum is the momentum possessed by purple ball only. After collision purple ball moves with velocity v 1prime in the positive X Y plane making an angle theta 1 with the x axis and the orange ball moves in the X Y plane below the x axis making an angle theta 2 with the x axis. The total momentum would be the sum of the momentum of purple ball p1 prime and the orange ball p 2 prime. In two-dimensional collision too the momentum before and after collision remains the same. — Figure 57.1: A two-dimensional collision with the coordinate system chosen so that [latex]{m}_{2}[/latex] is initially at rest and [latex]{v}_{1}[/latex] is parallel to the [latex]x[/latex] -axis. This coordinate system is sometimes called the laboratory coordinate system, because many scattering experiments have a target that is stationary in the laboratory, while particles are scattered from it to determine the particles that make-up the target and how they are bound together. The particles may not be observed directly, but their initial and final velocities are.

Conservation of Momentum Along the [latex]x[/latex]-Axis

[latex]{m}_{1}{v}_{1} = {m}_{1}{v\prime}_{1} \cos \theta_{1} + {m}_{2}{v\prime}_{2} \cos \theta_{2}[/latex]

This equation reflects the fact that only the [latex]x[/latex]-component of the momentum was nonzero initially. All motion along the [latex]x[/latex]-axis must still add up to the original momentum after the collision.

Conservation of Momentum Along the [latex]y[/latex]-Axis

[latex]0 = {m}_{1}{v\prime}_{1} \sin \theta_{1} + {m}_{2}{v\prime}_{2} \sin \theta_{2}[/latex]

Since both particles were initially moving only along the [latex]x[/latex]-axis, there was no initial [latex]y[/latex]-component of momentum. Therefore, any upward momentum after the collision must be exactly canceled by an equal downward momentum.

These two equations allow us to analyze and solve for unknowns like final speeds and directions, assuming known masses and initial velocities. However, with two equations, we can only solve for two unknowns—additional information (such as energy conservation) may be required to fully determine the outcome of the collision.

In practice, this two-dimensional approach is widely used in health science research—such as analyzing the motion of particles in medical imaging systems or modeling collisions between red blood cells in capillaries. Even in biomechanics, understanding two-dimensional interactions helps in studying how forces propagate through joints during movement or injury.

Example 57.1: Determining the Final Velocity of an Unseen Object from the Scattering of Another Object

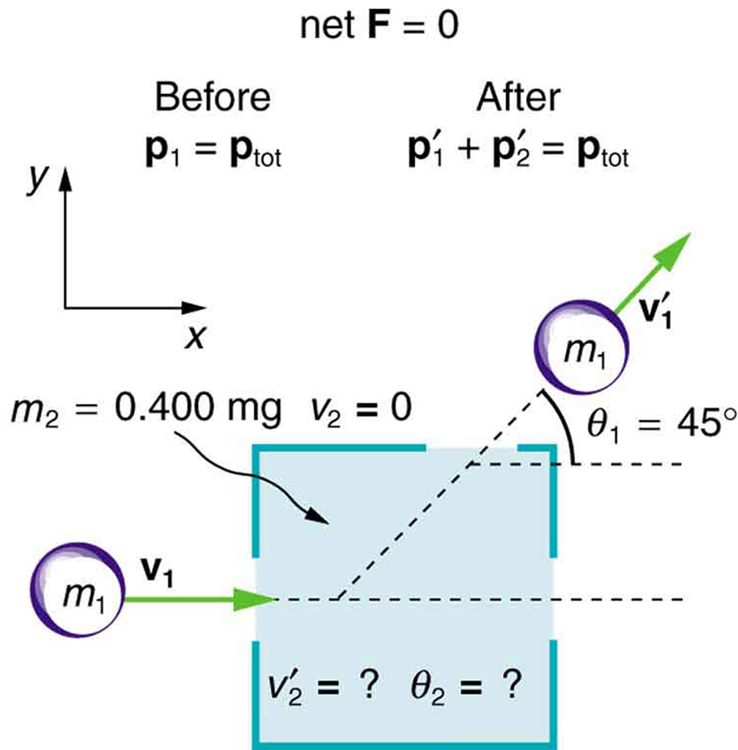
Suppose the following experiment is performed. A 0.250-kg object [latex]({m}_{1})[/latex] is slid on a frictionless surface into a dark room, where it strikes an initially stationary object with mass of 0.400 kg [latex]({m}_{2})[/latex]. The 0.250-kg object emerges from the room at an angle of [latex]\text{45}\text{.}0º[/latex] with its incoming direction.

The speed of the 0.250-kg object is originally 2.00 m/s and is 1.50 m/s after the collision. Calculate the magnitude and direction of the velocity [latex]({v\prime }_{2}^{}[/latex] and [latex]{\theta }_{2})[/latex] of the 0.400-kg object after the collision.

Strategy

Momentum is conserved because the surface is frictionless. The coordinate system shown in Figure 57.2 is one in which [latex]{m}_{2}[/latex] is originally at rest and the initial velocity is parallel to the [latex]x[/latex]-axis, so that conservation of momentum along the [latex]x[/latex]– and [latex]y[/latex]-axes is applicable.

Everything is known in these equations except [latex]{v\prime }_{2}^{}[/latex] and [latex]{\theta }_{2}[/latex], which are precisely the quantities we wish to find. We can find two unknowns because we have two independent equations: the equations describing the conservation of momentum in the [latex]x[/latex]– and [latex]y[/latex]-directions.

Solution

Solving [latex]{m}_{1}{v}_{1}={m}_{1}{v\prime }_{1}^{}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}{\theta }_{1}+{m}_{2}{v\prime }_{2}^{}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}{\theta }_{2}[/latex] for [latex]{v}_{2}^{\prime }\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}{\theta }_{2}[/latex] and [latex]0={m}_{1}{v\prime }_{1}^{}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}{\theta }_{1}+{m}_{2}{v\prime }_{2}^{}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}{\theta }_{2}[/latex] for [latex]{v\prime }_{2}^{}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}{\theta }_{2}[/latex] and taking the ratio yields an equation (in which θ₂ is the only unknown quantity. Applying the identity [latex]\left(\text{tan}\phantom{\rule{0.25em}{0ex}}\theta =\frac{\text{sin}\phantom{\rule{0.25em}{0ex}}\theta }{\text{cos}\phantom{\rule{0.25em}{0ex}}\theta }\right)[/latex], we obtain:

[latex]\text{tan}\phantom{\rule{0.25em}{0ex}}{\theta }_{2}=\frac{{v\prime }_{1}^{}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}{\theta }_{1}}{{v\prime }_{1}^{}\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}{\theta }_{1}-{v}_{1}}.[/latex]

Entering known values into the previous equation gives

[latex]\text{tan}\phantom{\rule{0.25em}{0ex}}{\theta }_{2}=\frac{\left(1\text{.}\text{50}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)\left(0\text{.}\text{7071}\right)}{\left(1\text{.}\text{50}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)\left(0\text{.}\text{7071}\right)-2\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{m/s}}=-1\text{.}\text{129}.[/latex]

Thus,

[latex]{\theta }_{2}={\text{tan}}^{-1}\left(-1\text{.}\text{129}\right)=\text{311}\text{.}5º\approx \text{312º}.[/latex]

Angles are defined as positive in the counter clockwise direction, so this angle indicates that [latex]{m}_{2}[/latex] is scattered to the right in Figure 57.2, as expected (this angle is in the fourth quadrant). Either equation for the
[latex]x[/latex]– or
[latex]y[/latex]-axis can now be used to solve for
[latex]{v\prime }_{2}[/latex], but the latter equation is easiest because it has fewer terms.

[latex]{v\prime }_{2}^{}=-\frac{{m}_{1}}{{m}_{2}}{v\prime }_{1}^{}\frac{\text{sin}\phantom{\rule{0.25em}{0ex}}{\theta }_{1}}{\text{sin}\phantom{\rule{0.25em}{0ex}}{\theta }_{2}}[/latex]

Entering known values into this equation gives

[latex]{v\prime }_{2}^{}=-\left(\frac{0\text{.}\text{250}\phantom{\rule{0.25em}{0ex}}\text{kg}}{0\text{.}\text{400}\phantom{\rule{0.25em}{0ex}}\text{kg}}\right)\left(1\text{.}\text{50}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)\left(\frac{0\text{.}\text{7071}}{-0\text{.}\text{7485}}\right)\text{.}[/latex]

Thus,

[latex]{v\prime }_{2}^{}=0\text{.}\text{886}\phantom{\rule{0.25em}{0ex}}\text{m/s}.[/latex]

Discussion

It is instructive to calculate the internal kinetic energy of this two-object system before and after the collision. (This calculation is left as an end-of-chapter problem.) If you do this calculation, you will find that the internal kinetic energy is less after the collision, and so the collision is inelastic. This type of result makes a physicist want to explore the system further.

A purple ball of mass m1 and velocity v one moves in the right direction into a dark room. It collides with an object of mass m two of value zero point four zero milligrams which was initially at rest and then leaves the dark room from the top right hand side making an angle of forty-five degrees with the horizontal and at velocity v one prime. The net external force on the system is zero. The momentum before and after collision remains the same. The velocity v two prime of the mass m two and the angle theta two it would make with the horizontal after collision not given. — Figure 57.2: A collision taking place in a dark room is explored. The incoming object [latex]{m}_{1}[/latex] is scattered by an initially stationary object. Only the stationary object’s mass [latex]{m}_{2}[/latex] is known. By measuring the angle and speed at which [latex]{m}_{1}[/latex] emerges from the room, it is possible to calculate the magnitude and direction of the initially stationary object’s velocity after the collision.

Elastic Collisions of Two Objects with Equal Mass

Some especially insightful results occur when two colliding objects have equal mass and the collision is elastic—that is, internal kinetic energy is conserved. This scenario applies closely to real-world systems such as colliding billiard balls, and more precisely, to particle interactions in subatomic physics. Understanding this simple case allows us to grasp more complex systems, including those found in molecular and cellular dynamics.

Let’s analyze a collision where two objects, each with mass [latex]m[/latex], interact (Refer to Figure 57.1 for masses and angles.). We assume object 2 is initially at rest. For an elastic collision, internal kinetic energy is conserved, so the total kinetic energy before and after the collision is equal:

[latex]\frac{1}{2}mv_1^2 = \frac{1}{2}mv_1^{\prime 2} + \frac{1}{2}mv_2^{\prime 2}[/latex]

Because both objects have the same mass, the equation simplifies, and we can factor out [latex]m[/latex] across all terms. From momentum conservation in both the [latex]x[/latex]– and [latex]y[/latex]-directions, we can also derive an expression that includes the angle between the two scattered particles:

[latex]\frac{1}{2}mv_1^2 = \frac{1}{2}mv_1^{\prime 2} + \frac{1}{2}mv_2^{\prime 2} + mv_1^\prime v_2^\prime \cos(\theta_1 - \theta_2)[/latex]

For both energy and momentum conservation to be satisfied simultaneously, this final term must equal zero:

[latex]mv_1^\prime v_2^\prime \cos(\theta_1 - \theta_2) = 0[/latex]

This product equals zero if at least one of the following conditions is true:

Head-on stop: [latex]v_1^\prime = 0[/latex] — the incoming object stops and transfers all momentum to the target.
No collision: [latex]v_2^\prime = 0[/latex] — the incoming object continues unaffected.
Right-angle scattering: [latex]\cos(\theta_1 - \theta_2) = 0[/latex] — meaning the angle between the outgoing velocities is [latex]90^\circ[/latex].

These results are remarkably consistent with observations in billiards and pool. For example, in a clean collision with no spin, the two balls often separate at a right angle, illustrating the conservation of momentum and internal kinetic energy. In reality, spin introduces additional complexities like rotational energy and angular momentum, which we will address in later chapters.

This idealized case also has strong parallels in biology and medicine. When modeling elastic interactions between molecules—such as gas particles in the lungs or intracellular vesicle motion—assuming equal masses can simplify calculations without losing meaningful accuracy.

Connections to Nuclear and Particle Physics

Two-dimensional collision experiments are foundational to modern nuclear and particle physics. For instance, Ernest Rutherford’s gold foil experiment used particle scattering to reveal the atomic nucleus, a discovery that redefined our understanding of matter. Today, similar methods are used in particle accelerators to uncover the properties of fundamental particles, many of which interact through elastic collisions.

Section Summary

In two-dimensional collisions, the analysis is simplified by selecting a convenient coordinate system—typically one with the [latex]x[/latex]-axis aligned with the initial velocity of the incoming object. This allows the motion to be resolved into independent components along perpendicular axes.
For two-dimensional collisions involving point masses—which are idealized, structureless particles that cannot rotate—and where object 2 is initially at rest, the momentum is conserved independently along each axis.
Momentum conservation along the initial direction of motion (the [latex]x[/latex]-axis) is given by:
[latex]m_1 v_1 = m_1 v_1^{\prime} \cos \theta_1 + m_2 v_2^{\prime} \cos \theta_2[/latex]
Momentum conservation along the perpendicular direction (the [latex]y[/latex]-axis) is expressed as:
[latex]0 = m_1 v_1^{\prime} \sin \theta_1 + m_2 v_2^{\prime} \sin \theta_2[/latex]
For elastic collisions between two objects of equal mass, conservation of internal kinetic energy leads to:
[latex]\frac{1}{2}mv_1^2 = \frac{1}{2}mv_1^{\prime 2} + \frac{1}{2}mv_2^{\prime 2} + mv_1^{\prime} v_2^{\prime} \cos(\theta_1 - \theta_2)[/latex]

Conceptual Questions

Figure 57.3 shows a cube at rest and a small object heading toward it. (a) Describe the directions (angle [latex]{\theta }_{1}[/latex]) at which the small object can emerge after colliding elastically with the cube. How does [latex]{\theta }_{1}[/latex] depend on [latex]b[/latex], the so-called impact parameter? Ignore any effects that might be due to rotation after the collision, and assume that the cube is much more massive than the small object. (b) Answer the same questions if the small object instead collides with a massive sphere.

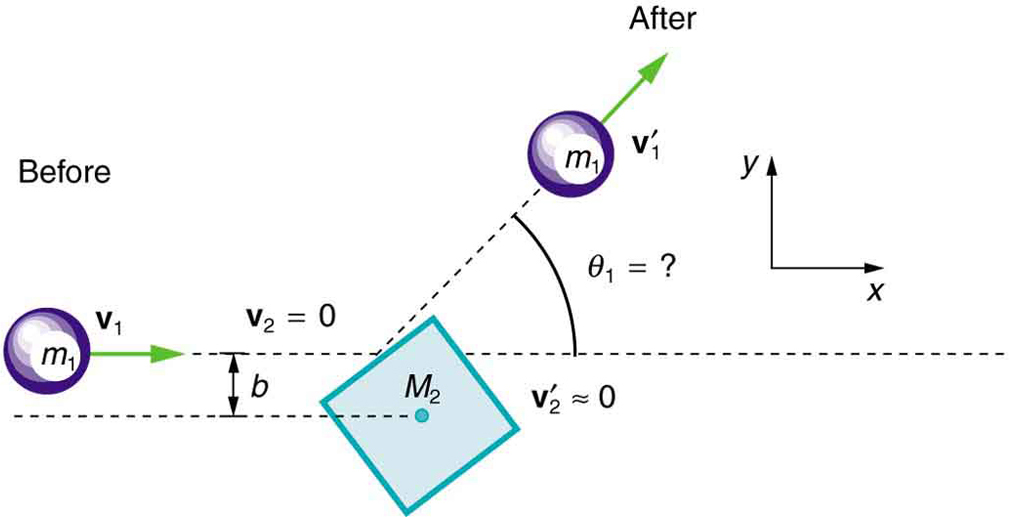
Figure 57.3: A small object approaches a collision with a much more massive cube, after which its velocity has the direction [latex]{\theta }_{1}[/latex]. The angles at which the small object can be scattered are determined by the shape of the object it strikes and the impact parameter [latex]b[/latex].

Problems & Exercises

Two identical pucks collide on an air hockey table. One puck was originally at rest. (a) If the incoming puck has a speed of 6.00 m/s and scatters to an angle of [latex]\text{30}\text{.}0º[/latex],what is the velocity (magnitude and direction) of the second puck? (You may use the result that [latex]{\theta }_{1}-{\theta }_{2}=\text{90º}[/latex] for elastic collisions of objects that have identical masses.) (b) Confirm that the collision is elastic.
A 3000-kg cannon is mounted so that it can recoil only in the horizontal direction. (a) Calculate its recoil velocity when it fires a 15.0-kg shell at 480 m/s at an angle of [latex]\text{20}\text{.}0º[/latex] above the horizontal. (b) What is the kinetic energy of the cannon? This energy is dissipated as heat transfer in shock absorbers that stop its recoil. (c) What happens to the vertical component of momentum that is imparted to the cannon when it is fired?
Professional Application A 5.50-kg bowling ball moving at 9.00 m/s collides with a 0.850-kg bowling pin, which is scattered at an angle of [latex]\text{85}\text{.}0º[/latex] to the initial direction of the bowling ball and with a speed of 15.0 m/s. (a) Calculate the final velocity (magnitude and direction) of the bowling ball. (b) Is the collision elastic? (c) Linear kinetic energy is greater after the collision. Discuss how spin on the ball might be converted to linear kinetic energy in the collision.
Professional Application Ernest Rutherford (the first New Zealander to be awarded the Nobel Prize in Chemistry) demonstrated that nuclei were very small and dense by scattering helium-4 nuclei [latex]\left({}^{4}\text{He}\right)[/latex] from gold-197 nuclei [latex]\left({}^{\text{197}}\text{Au}\right)[/latex]. The energy of the incoming helium nucleus was [latex]8.00×{\text{10}}^{-\text{13}}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex], and the masses of the helium and gold nuclei were [latex]6.68×{\text{10}}^{-\text{27}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] and [latex]3.29×{\text{10}}^{-\text{25}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex], respectively (note that their mass ratio is 4 to 197). (a) If a helium nucleus scatters to an angle of [latex]\text{120º}[/latex] during an elastic collision with a gold nucleus, calculate the helium nucleus’s final speed and the final velocity (magnitude and direction) of the gold nucleus. (b) What is the final kinetic energy of the helium nucleus?
Professional Application Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1200 kg and is approaching at [latex]8\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex] due south. The second car has a mass of 850 kg and is approaching at [latex]\text{17}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex] due west. (a) Calculate the final velocity (magnitude and direction) of the cars. (b) How much kinetic energy is lost in the collision? (This energy goes into deformation of the cars.) Note that because both cars have an initial velocity, you cannot use the equations for conservation of momentum along the [latex]x[/latex]-axis and [latex]y[/latex]-axis; instead, you must look for other simplifying aspects.
Integrated Concepts A 90.0-kg ice hockey player hits a 0.150-kg puck, giving the puck a velocity of 45.0 m/s. If both are initially at rest and if the ice is frictionless, how far does the player recoil in the time it takes the puck to reach the goal 15.0 m away?