"

Rotational motion and angular momentum

69 Collisions of Extended Bodies in Two Dimensions

Learning Objectives

  • Observe collisions of extended bodies in two dimensions.
  • Examine collision at the point of percussion.

Bowling pins are sent flying and spinning when struck by a bowling ball—both angular momentum and linear momentum, along with energy, are transferred to the pins (Figure 69.1). Many real-world collisions involve rotational motion. For example, a car sliding on ice may start to spin as it collides with another vehicle. In sports, pitchers throw curveballs by imparting spin, and tennis players generate topspin to control ball trajectory. These situations all involve collisions that include angular motion.

Let’s analyze a relatively simple rotational collision shown in Figure 69.2. A small disk slides toward and sticks to an initially stationary stick that is pinned at one end on a frictionless surface. After the collision, the combined system begins to rotate around the fixed pivot point (the nail). While there is an external force at the pivot, it exerts no torque because the lever arm [latex]r[/latex] is zero at the pivot point. As a result, angular momentum is conserved during the collision. However, since the disk adheres to the stick, this is an inelastic collision, so mechanical energy is not conserved. Additionally, linear momentum may not be conserved in the direction of the incoming disk if the pivot applies a horizontal force. We’ll work through the mechanics of this in Example 69.1.

A bowling ball, just as it is striking the pins.
Figure 69.1: The bowling ball causes the pins to scatter, many of them spinning violently. Angular momentum is transferred along with linear momentum. (credit: Tinou Bao, Flickr)
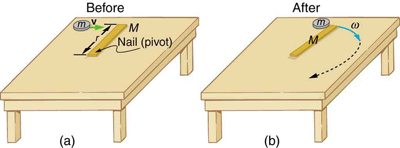
Figure a shows a disc m sliding toward a motionless stick M of length r pivoted about a nail, on a frictionless surface. In figure b, a disk hits the stick at one end and adheres to it, and the stick rotates, pivoting around the nail in a direction shown by the arrow in the clockwise direction and angular velocity omega.
Figure 69.2: (a) A disk slides toward a stationary stick on a frictionless surface. (b) Upon impact, the disk adheres to the stick, and together they rotate around the fixed pivot. Angular momentum is conserved because no external torque is exerted at the pivot.

Example 69.1: Rotation in a Collision

Suppose the disk in Figure 69.2 has a mass of 50.0 g and an initial velocity of 30.0 m/s when it strikes the stick that is 1.20 m long and 2.00 kg.

(a) What is the angular velocity of the two after the collision?

(b) What is the kinetic energy before and after the collision?

(c) What is the total linear momentum before and after the collision?

Strategy for (a)

We can answer the first question using conservation of angular momentum as noted. Because angular momentum is [latex]\mathrm{I\omega }[/latex], we can solve for angular velocity.

Solution for (a)

Conservation of angular momentum states

[latex]L=L\prime ,[/latex]

where primed quantities stand for conditions after the collision and both momenta are calculated relative to the pivot point. The initial angular momentum of the system of stick-disk is that of the disk just before it strikes the stick. That is,

[latex]L=\mathrm{I\omega },[/latex]

where [latex]I[/latex] is the moment of inertia of the disk and [latex]\omega[/latex] is its angular velocity around the pivot point. Now, [latex]I={\text{mr}}^{\mathrm{\text{2}}}[/latex] (taking the disk to be approximately a point mass) and [latex]\omega =v/r[/latex], so that

[latex]L={\text{mr}}^{2}\frac{v}{r}=\text{mvr}.[/latex]

After the collision,

[latex]L\prime =I\prime \omega \prime .[/latex]

It is [latex]\omega \prime[/latex]
that we wish to find. Conservation of angular momentum gives

[latex]I\prime \omega \prime =\text{mvr}.[/latex]

Rearranging the equation yields

[latex]\omega \prime =\frac{\text{mvr}}{I\prime },[/latex]

where [latex]I\prime[/latex] is the moment of inertia of the stick and disk stuck together, which is the sum of their individual moments of inertia about the nail. Dynamics of Rotational Motion: Rotational Inertia gives the formula for a rod rotating around one end to be [latex]I={\text{Mr}}^{2}/3[/latex]. Thus,

[latex]I\prime ={\text{mr}}^{2}+\frac{{\text{Mr}}^{2}}{3}=\left(m+\frac{M}{3}\right){r}^{2}.[/latex]

Entering known values in this equation yields,

[latex]I\text{′}=\left(0\text{.}\text{0500}\phantom{\rule{0.25em}{0ex}}\text{kg}+0\text{.}\text{667 kg}\right){\left(1\text{.}\text{20}\phantom{\rule{0.25em}{0ex}}\text{m}\right)}^{2}=1\text{.}\text{032}\phantom{\rule{0.25em}{0ex}}\text{kg}\cdot {\text{m}}^{2}.[/latex]

The value of [latex]I\prime[/latex] is now entered into the expression for
[latex]\omega \prime[/latex], which yields

[latex]\begin{array}{lll}\omega \prime & =& \frac{\text{mvr}}{I\prime }=\frac{\left(0\text{.}\text{0500 kg}\right)\left(\text{30}\text{.}0 m/s\right)\left(1\text{.}\text{20 m}\right)}{1\text{.}\text{032 kg}\cdot {\text{m}}^{2}}\\ & =& 1\text{.}\text{744 rad/s}\approx 1\text{.}\text{74 rad/s}.\end{array}[/latex]

Strategy for (b)

The kinetic energy before the collision is the incoming disk’s translational kinetic energy, and after the collision, it is the rotational kinetic energy of the two stuck together.

Solution for (b)

First, we calculate the translational kinetic energy by entering given values for the mass and speed of the incoming disk.

[latex]\text{KE}=\frac{1}{2}{\text{mv}}^{2}=\left(0\text{.}\text{500}\right)\left(0\text{.}\text{0500}\phantom{\rule{0.25em}{0ex}}\text{kg}\right){\left(\text{30}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)}^{2}=\text{22.5 J}[/latex]

After the collision, the rotational kinetic energy can be found because we now know the final angular velocity and the final moment of inertia. Thus, entering the values into the rotational kinetic energy equation gives

[latex]\begin{array}{lll}\text{KE′}& =& \frac{1}{2}I\prime {\omega \prime }^{2}=\left(0.5\right)\left(1.032\phantom{\rule{0.25em}{0ex}}\text{kg}\cdot {\text{m}}^{2}\right){\left(1\text{.}\text{744}\frac{\text{rad}}{\text{s}}\right)}^{2}\\ & =& \text{1.57 J.}\end{array}[/latex]

Strategy for (c)

The linear momentum before the collision is that of the disk. After the collision, it is the sum of the disk’s momentum and that of the center of mass of the stick.

Solution of (c)

Before the collision, then, linear momentum is

[latex]p=\text{mv}=\left(0\text{.}\text{0500}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)\left(\text{30}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)=1\text{.}\text{50}\phantom{\rule{0.25em}{0ex}}\text{kg}\cdot \text{m/s}.[/latex]

After the collision, the disk and the stick’s center of mass move in the same direction. The total linear momentum is that of the disk moving at a new velocity [latex]v\prime =\mathrm{r\omega }\prime[/latex] plus that of the stick’s center of mass,

which moves at half this speed because [latex]{v}_{\text{CM}}=\left(\frac{r}{2}\right)\omega \prime =\frac{v\prime }{2}[/latex]. Thus,

[latex]p\prime =\text{mv}\prime +{\text{Mv}}_{\text{CM}}=\text{mv}\prime +\frac{\text{Mv}\prime }{2}.[/latex]

Gathering similar terms in the equation yields,

[latex]p\prime =\left(m+\frac{M}{2}\right)v\prime[/latex]

so that

[latex]p\prime =\left(m+\frac{M}{2}\right)\mathrm{r\omega }\prime .[/latex]

Substituting known values into the equation,

[latex]p\prime =\left(1\text{.}\text{050 kg}\right)\left(1\text{.}\text{20}\phantom{\rule{0.25em}{0ex}}\text{m}\right)\left(1\text{.}\text{744 rad/s}\right)=\text{2.20 kg}\cdot \text{m/s}.[/latex]

Discussion

First note that the kinetic energy is less after the collision, as predicted, because the collision is inelastic. More surprising is that the momentum after the collision is actually greater than before the collision. This result can be understood if you consider how the nail affects the stick and vice versa. Apparently, the stick pushes backward on the nail when first struck by the disk. The nail’s reaction (consistent with Newton’s third law) is to push forward on the stick, imparting momentum to it in the same direction in which the disk was initially moving, thereby increasing the momentum of the system.

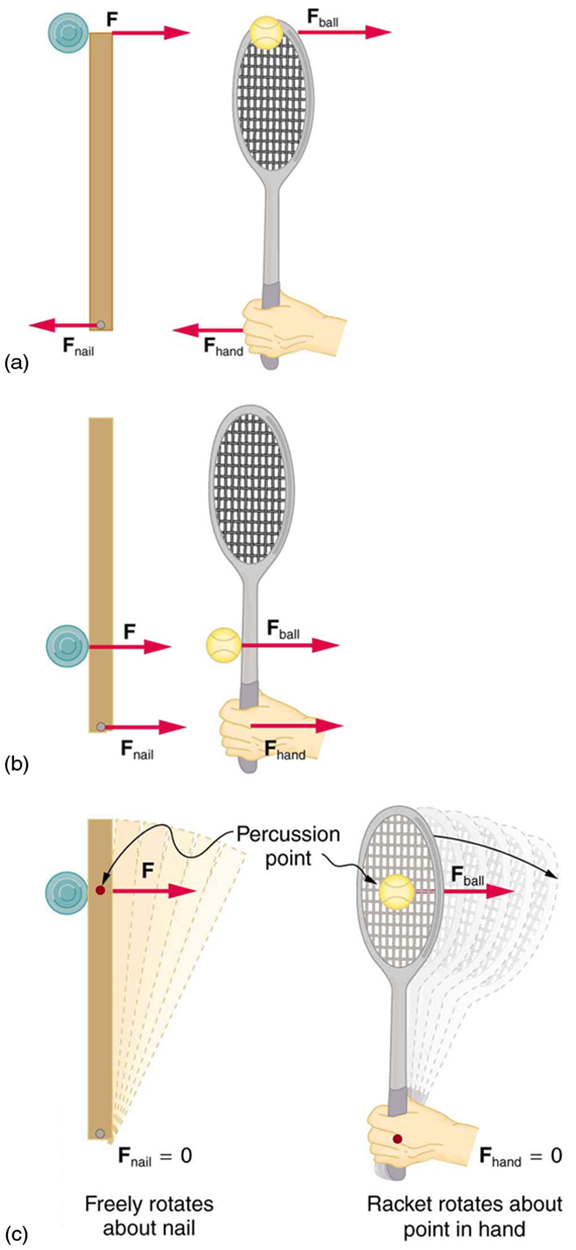
In the previous example, we saw that the point of impact affects how forces are transmitted through a rotating object. What would happen if the disk collided very close to the nail? In this case, a forward force would be exerted on the nail. Conversely, if the impact occurred at the far end of the stick, a backward force would result. This tells us that there must be a specific impact point—somewhere between these two extremes—where no force is transmitted to the pivot. This special location is known as the percussion point.

This concept is common in sports. Take tennis, for example. When a tennis ball hits the racquet near the head, the handle tends to pull away from the player’s hand. When the ball strikes lower on the shaft, the handle pushes into the hand. But when the ball hits exactly at the percussion point—sometimes called the “sweet spot”—there’s minimal or no force felt at the grip. Hitting the sweet spot reduces vibration and the risk of injury (like tennis elbow). The same principle applies to baseball bats and golf clubs, as shown in Figure 69.3.

In figure a, a disk hitting a stick is compared to a tennis ball being hit by a racquet. When the ball strikes the racquet near the end with a force denoted by f ball as shown by the direction of the arrow, a backward force, f hand is exerted on the hand, In figure b, when the racquet is struck much farther down by a force F ball, a forward force, f hand is exerted on the hand as shown by the arrows. In figure (c), when the racquet is struck by the ball with a force f ball at the percussion point, no force is delivered to the hand. This implies that f hand is equal to zero.
Figure 69.3: When a tennis racquet strikes a ball near the end (a), a backward force is felt at the grip. When the ball strikes near the handle (b), a forward force is exerted. When the ball hits at the racquet’s percussion point (c), no force is transferred to the hand. This is the “sweet spot” in racquet design.

Check Your Understanding

Question: Is rotational kinetic energy a vector? Justify your answer.

Answer: No, energy is always a scalar. It has magnitude but no direction in space. Rotational kinetic energy, like linear kinetic energy, depends only on the speed of rotation—not the direction.

Section Summary

  • Angular momentum [latex]L[/latex] is analogous to linear momentum and is given by [latex]L = I \omega[/latex].
  • Angular momentum changes when torque is applied, following the relationship:
    [latex]\text{net}\ \tau = \frac{\Delta L}{\Delta t}[/latex]
  • Angular momentum is conserved when the net external torque is zero:
    [latex]L = \text{constant} \quad (\text{if}\ \text{net}\ \tau = 0)[/latex]

    or equivalently,

    [latex]L = L' \quad (\text{if}\ \text{net}\ \tau = 0)[/latex]

    This is known as the law of conservation of angular momentum, and it applies in rotational collisions and isolated systems.

Conceptual Questions

  1. Describe two different collisions—one in which angular momentum is conserved, and the other in which it is not. Which condition determines whether or not angular momentum is conserved in a collision?
  2. Suppose an ice hockey puck strikes a hockey stick that lies flat on the ice and is free to move in any direction. Which quantities are likely to be conserved: angular momentum, linear momentum, or kinetic energy (assuming the puck and stick are very resilient)?
  3. While driving his motorcycle at highway speed, a physics student notices that pulling back lightly on the right handlebar tips the cycle to the left and produces a left turn. Explain why this happens.

Problems & Exercises

  1. Repeat Example 69.1 in which the disk strikes and adheres to the stick 0.100 m from the nail.
  2. Repeat Example 69.1 in which the disk originally spins clockwise at 1000 rpm and has a radius of 1.50 cm.
  3. Twin skaters approach one another as shown in Figure 69.4 and lock hands. (a) Calculate their final angular velocity, given each had an initial speed of 2.50 m/s relative to the ice. Each has a mass of 70.0 kg, and each has a center of mass located 0.800 m from their locked hands. You may approximate their moments of inertia to be that of point masses at this radius. (b) Compare the initial kinetic energy and final kinetic energy.
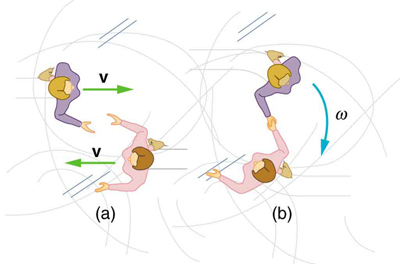
    Figure a shows two skaters from the top view approaching each other from opposite directions with velocity v. In figure b two skaters then lock their right hands and start to spin in the clockwise direction with angular velocity omega.
    Figure 69.4: Twin skaters approach each other with identical speeds. Then, the skaters lock hands and spin.
  4. Suppose a 0.250-kg ball is thrown at 15.0 m/s to a motionless person standing on ice who catches it with an outstretched arm as shown in Figure 69.5. (a) Calculate the final linear velocity of the person, given his mass is 70.0 kg. (b) What is his angular velocity if each arm is 5.00 kg? You may treat the ball as a point mass and treat the person’s arms as uniform rods (each has a length of 0.900 m) and the rest of his body as a uniform cylinder of radius 0.180 m. Neglect the effect of the ball on his center of mass so that his center of mass remains in his geometrical center. (c) Compare the initial and final total kinetic energies.
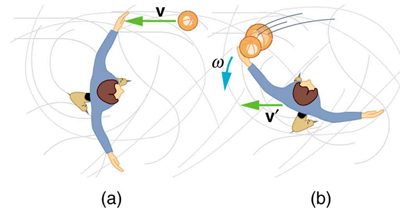
    Figure a shows a skater through an overhead view with both his hands outstretched. A ball is seen approaching toward him in air with velocity v. Figure b shows that skater catching two balls in his left hand, and then, recoiling toward the left, in clockwise direction, with angular velocity omega and finally, the balls have velocity v prime.
    Figure 69.5: The figure shows the overhead view of a person standing motionless on ice about to catch a ball. Both arms are outstretched. After catching the ball, the skater recoils and rotates.
  5. Repeat Example 69.1 in which the stick is free to have translational motion as well as rotational motion.

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book