"

Thermodynamics

111 Carnot’s Perfect Heat Engine: The Second Law of Thermodynamics Restated

Learning Objectives

  • Identify a Carnot cycle and its characteristics on a PV diagram.
  • Calculate the theoretical maximum efficiency of a heat engine, such as a nuclear reactor.
  • Describe how real-world dissipative processes reduce the efficiency of engines below the Carnot ideal.
Photograph of a novelty toy known as the drinking bird. It is made up of two glass bulbs connected to each other by a glass tube. The upper bulb is shaped like a bird’s head, and the tube looks like its neck. The lower bulb, which may be compared to the abdomen, contains methylene chloride that has been colored red. The bottom of the neck is attached to a pivot, and in front of the bird’s head is a glass of water.
Figure 111.1: The drinking bird toy is a real-world example of a simplified Carnot engine. It operates through a continuous heat transfer cycle involving evaporation and condensation of a low-boiling-point liquid. Though not truly perpetual motion, it offers an accessible demonstration of cyclic thermodynamic principles. (credit: Arabesk.nl, Wikimedia Commons)

According to the second law of thermodynamics, no heat engine can be 100% efficient—some portion of heat energy must always be rejected to a cooler environment, called the waste heat. This raises the question: What is the theoretical maximum efficiency any engine can achieve? In 1824, French engineer Sadi Carnot answered this by developing a theoretical model—the Carnot cycle—that defines the upper limit of efficiency for any cyclic heat engine.

An engine that follows the Carnot cycle is known as a Carnot engine. This cycle is composed exclusively of reversible processes: two isothermal processes (constant temperature) and two adiabatic processes (no heat exchange). Real-world engines, by contrast, experience dissipative effects like friction, turbulence, and rapid expansion that introduce irreversibility and reduce efficiency.

Carnot Engine

One form of the second law of thermodynamics states: A Carnot engine operating between two given temperatures achieves the maximum possible efficiency of any engine working between those same temperatures. Any real engine that uses only reversible processes will match the Carnot engine’s efficiency under identical thermal conditions.

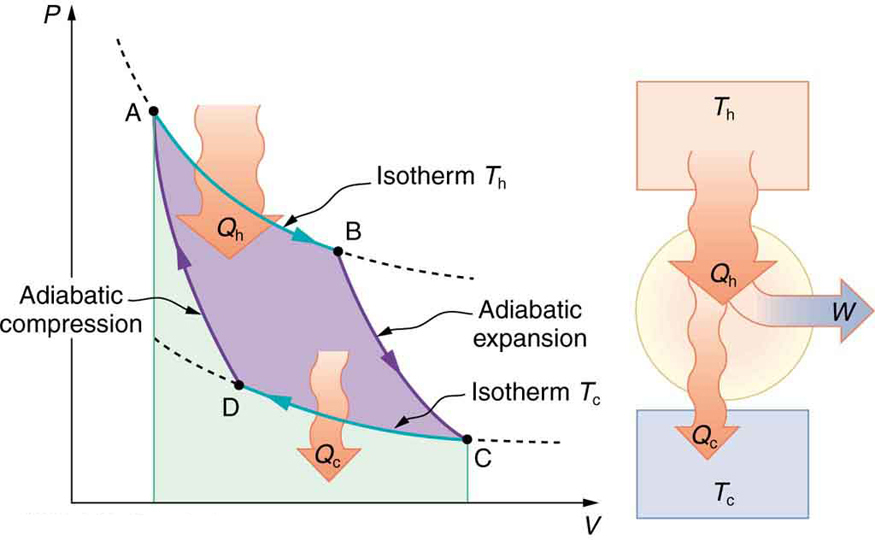
Figure 111.2 illustrates the Carnot cycle on a pressure-volume ([latex]PV[/latex]) diagram. The working substance undergoes two isothermal changes (AB and CD) and two adiabatic changes (BC and DA). Heat is absorbed at the higher temperature [latex]T_{\text{h}}[/latex] during AB and released at the lower temperature [latex]T_{\text{c}}[/latex] during CD. The area enclosed by the cycle represents the net mechanical work done by the system.

The efficiency of any cyclic heat engine is given by:

[latex]\text{Eff} = \frac{Q_{\text{h}} - Q_{\text{c}}}{Q_{\text{h}}} = 1 - \frac{Q_{\text{c}}}{Q_{\text{h}}}[/latex]

What Carnot showed is that for a perfect (ideal) heat engine, the ratio of heat expelled to heat absorbed is equal to the ratio of the absolute temperatures of the cold and hot reservoirs:

[latex]\frac{Q_{\text{c}}}{Q_{\text{h}}} = \frac{T_{\text{c}}}{T_{\text{h}}}[/latex]

So, the Carnot efficiency becomes:

[latex]\mathrm{Eff}_{\text{C}} = 1 - \frac{T_{\text{c}}}{T_{\text{h}}}[/latex]

Here, both [latex]T_{\text{c}}[/latex] and [latex]T_{\text{h}}[/latex] must be measured in kelvins (or any other absolute temperature scale). This equation defines the theoretical upper limit for efficiency between two temperatures. In practice, most engines reach about 70% of this maximum efficiency.

This result implies that 100% efficiency is only possible if the cold reservoir is at absolute zero ([latex]T_{\text{c}} = 0 \, \text{K}[/latex]), which is unattainable both practically and theoretically. Thus, all real heat engines must expel some portion of their energy as waste heat.

To maximize efficiency in a real-world system, we aim to make the ratio [latex]T_{\text{c}}/T_{\text{h}}[/latex] as small as possible. This can be done by:

  • Increasing the temperature of the heat source ([latex]T_{\text{h}}[/latex])
  • Decreasing the temperature of the heat sink ([latex]T_{\text{c}}[/latex])

These strategies are consistent with those discussed for the Otto cycle: a greater temperature difference between heat source and sink leads to higher net work output and better efficiency. The challenge in engineering lies in achieving high temperature differentials without compromising safety or material stability.

Part a of the figure shows a graph of pressure P versus volume V for a Carnot cycle. The pressure P is along the Y axis and the volume V is along the X axis. The graph shows a complete cycle A B C D. The path begins at point A, then it moves smoothly down till point B along the direction of the X axis. This is marked as an isotherm at temperature T sub h. Then the curve drops down further, along a different curve, from point B to point C. This is marked as adiabatic expansion. The curve rises from point C to point D along the direction opposite to that of A B. This is also an isotherm but at temperature T sub c. The last part of the curve rises up from point D back to A along a direction opposite to that of B C. This is marked as adiabatic compression. The path C D is lower than path A B. Heat Q sub h enters the system, as shown by a bold arrow to the curve A B. Heat Q sub c leaves the system as shown by a bold arrow near C D. Part b of the diagram shows an internal combustion engine represented as a circle. The hot reservoir is a rectangular section at the top of the circle shown at temperature T sub h. A cold reservoir is shown as a rectangular section in the bottom part of the circle at temperature T sub c. Heat Q sub h enters the heat engine as shown by a bold arrow; work W is produced as output, shown to leave the system, and the remaining heat Q sub c is returned back to the cold reservoir, as shown by a bold arrow toward it.
Figure 111.2: The [latex]PV[/latex] diagram of a Carnot cycle shows two isothermal and two adiabatic processes. Heat [latex]Q_{\text{h}}[/latex] enters the system during the isothermal expansion AB at temperature [latex]T_{\text{h}}[/latex], and heat [latex]Q_{\text{c}}[/latex] exits the system during the isothermal compression CD at temperature [latex]T_{\text{c}}[/latex]. The net work output is represented by the area inside the loop. Also shown is a schematic of a Carnot engine operating between thermal reservoirs at [latex]T_{\text{h}}[/latex] and [latex]T_{\text{c}}[/latex].

Example 111.1 Maximum Theoretical Efficiency for a Nuclear Reactor

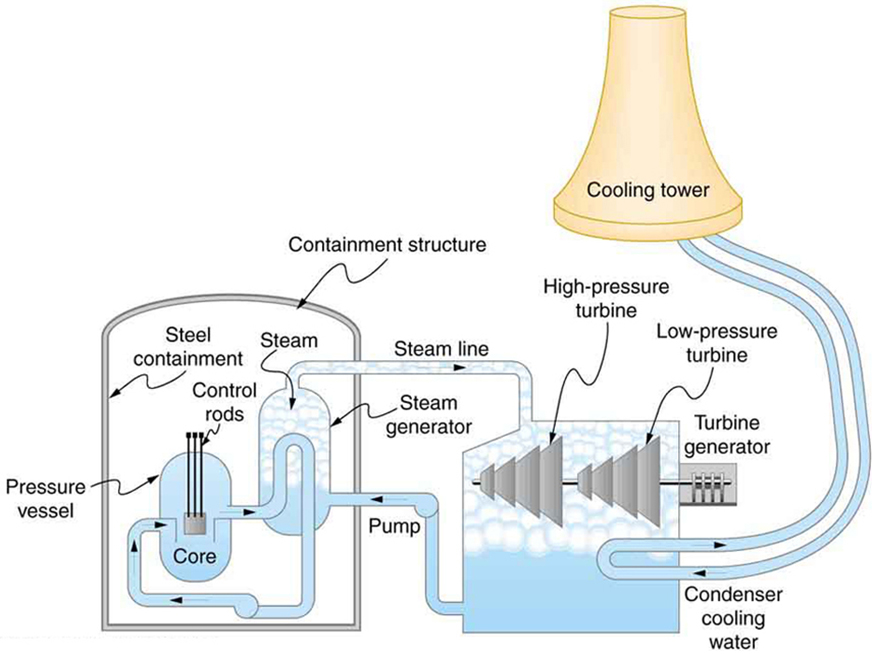
A nuclear power reactor has pressurized water at [latex]\text{300}\text{º}\text{C}[/latex]. (Higher temperatures are theoretically possible but practically not, due to limitations with materials used in the reactor.) Heat transfer from this water is a complex process (see Figure 111.3). Steam, produced in the steam generator, is used to drive the turbine-generators. Eventually the steam is condensed to water at [latex]\text{27}\text{º}\text{C}[/latex] and then heated again to start the cycle over. Calculate the maximum theoretical efficiency for a heat engine operating between these two temperatures.

Diagram shows a schematic diagram of a pressurized water nuclear reactor and the steam turbines that convert work into electrical energy. There is a pressure vessel in the middle, dome shaped at the ends. This has a nuclear core in it. The core is a small square in the center of the reactor. Control rods are shown as sticks of equal length attached to the core. The pressure vessel has some coolant tubes passing through it and then back to a steam chamber. These coolant tubes contain a coolant liquid that transports the heat from the pressure vessel to the steam chamber. This whole system is enclosed in another dome shaped containment structure of steel. The water supply to steam chamber and the steam outlet are seen to come out of this chamber. This steam is now shown to run two steam turbines, one a high pressure one and another low pressure one. The turbines are nearly triangular and segmented in shape. The steam turbine in turn generates power using a turbine generator, which is attached to the turbine system. The turbines are again housed in another chamber which gets the steam from the steam chamber and return the steam as water back to the steam chamber with pipes. A coolant tower is shown near the turbine system, which is shown to supply cool water in tubes to the turbine system to cool the steam back to water.
Figure 111.3: Schematic diagram of a pressurized water nuclear reactor and the steam turbines that convert work into electrical energy. Heat exchange is used to generate steam, in part to avoid contamination of the generators with radioactivity. Two turbines are used because this is less expensive than operating a single generator that produces the same amount of electrical energy. The steam is condensed to liquid before being returned to the heat exchanger, to keep exit steam pressure low and aid the flow of steam through the turbines (equivalent to using a lower-temperature cold reservoir). The considerable energy associated with condensation must be dissipated into the local environment; in this example, a cooling tower is used so there is no direct heat transfer to an aquatic environment. (Note that the water going to the cooling tower does not come into contact with the steam flowing over the turbines.)

Strategy

Since temperatures are given for the hot and cold reservoirs of this heat engine, [latex]{\mathrm{Eff}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}[/latex] can be used to calculate the Carnot (maximum theoretical) efficiency. Those temperatures must first be converted to kelvins.

Solution

The hot and cold reservoir temperatures are given as [latex]\text{300}\text{º}\text{C}[/latex] and [latex]\text{27}\text{.}0\text{º}\text{C}[/latex], respectively. In kelvins, then, [latex]{T}_{\text{h}}=\text{573 K}[/latex] and

[latex]{T}_{\text{c}}=\text{300 K}[/latex], so that the maximum efficiency is

[latex]{\text{Eff}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}\text{.}[/latex]

Thus,

[latex]\begin{array}{lll}{\text{Eff}}_{\text{C}}& =& 1-\frac{\text{300 K}}{\text{573 K}}\\ & =& 0\text{.}\text{476}\text{, or }\text{47}\text{.}6\%\text{.}\end{array}[/latex]

Discussion

A typical nuclear power station’s actual efficiency is about 35%, a little better than 0.7 times the maximum possible value, a tribute to superior engineering. Electrical power stations fired by coal, oil, and natural gas have greater actual efficiencies (about 42%), because their boilers can reach higher temperatures and pressures. The cold reservoir temperature in any of these power stations is limited by the local environment. Figure 111.4 shows (a) the exterior of a nuclear power station and (b) the exterior of a coal-fired power station. Both have cooling towers into which water from the condenser enters the tower near the top and is sprayed downward, cooled by evaporation.

Part a shows a photograph of an operational nuclear power plant in night view. There are dome shaped structures which house radioactive material and vapors are shown to come from two cooling towers. Part b shows a photograph of a coal fired power plant. Several huge cooling towers are shown.
Figure 111.4: (a) A nuclear power station (credit: BlatantWorld.com) and (b) a coal-fired power station. Both have cooling towers in which water evaporates into the environment, representing [latex]{Q}_{\text{c}}[/latex]. The nuclear reactor, which supplies [latex]{Q}_{\text{h}}[/latex], is housed inside the dome-shaped containment buildings. (credit: Robert & Mihaela Vicol, publicphoto.org)

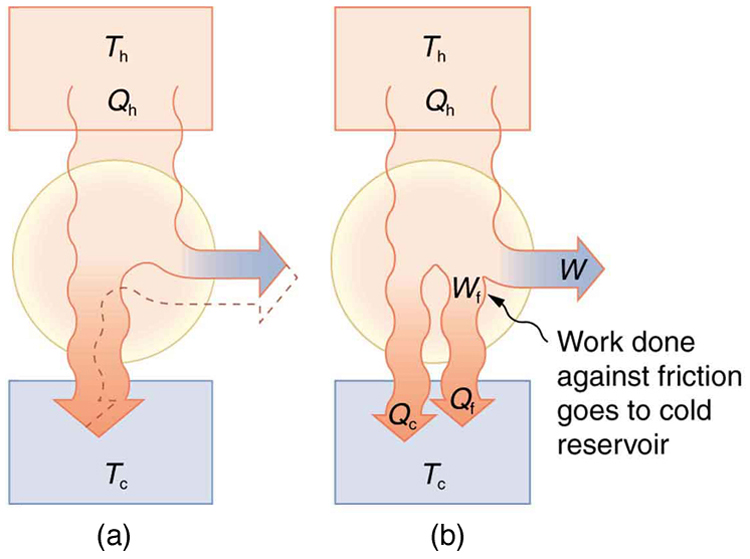
Since all real processes are irreversible, the actual efficiency of a heat engine can never be as great as that of a Carnot engine, as illustrated in Figure 111.5(a). Even with the best heat engine possible, there are always dissipative processes in peripheral equipment, such as electrical transformers or car transmissions. These further reduce the overall efficiency by converting some of the engine’s work output back into heat transfer, as shown in Figure 111.5(b).

Part a of the diagram shows a combustion engine represented as a circle to compare the efficiency of real and Carnot engines. The hot reservoir is a rectangular section above the circle shown at temperature T sub h. A cold reservoir is shown as a rectangular section below the circle at temperature T sub c. Heat Q sub h enters the heat engine as shown by a bold arrow. For a real engine a small part of it is shown to be expelled as output from the engine shown as a bold arrow leaving the circle and for a Carnot engine larger part of it is shown to leave as work shown by a dashed arrow leaving the circle. The remaining heat is shown to be returned back to the cold reservoir as shown by bold arrow toward it for real engines and comparatively lesser heat is given by the Carnot engine shown by a dashed arrow. Part b of the diagram shows an internal combustion engine represented as a circle to study friction and other dissipative processes in the output mechanisms of a heat engine. The hot reservoir is a rectangular section above the circle shown at temperature T sub h. A cold reservoir is shown as a rectangular section below the circle at temperature T sub c. Heat Q sub h enters the heat engine as shown by a bold arrow, work W is produced as output, shown leaving the system, and the remaining heat Q sub c and Q sub f are returned back to the cold reservoir as shown by bold arrows toward it. Q sub f is heat due to friction. The work done against friction goes as heat Q sub f to the cold reservoir.
Figure 111.5: Real heat engines are less efficient than Carnot engines. (a) Real engines use irreversible processes, reducing the heat transfer to work. Solid lines represent the actual process; the dashed lines are what a Carnot engine would do between the same two reservoirs. (b) Friction and other dissipative processes in the output mechanisms of a heat engine convert some of its work output into heat transfer to the environment.

Section Summary

  • The Carnot cycle is a theoretical cycle that is the most efficient cyclical process possible. Any engine using the Carnot cycle, which uses only reversible processes (adiabatic and isothermal), is known as a Carnot engine.
  • Any engine that uses the Carnot cycle enjoys the maximum theoretical efficiency.
  • While Carnot engines are ideal engines, in reality, no engine achieves Carnot’s theoretical maximum efficiency, since dissipative processes, such as friction, play a role. Carnot cycles without heat loss may be possible at absolute zero, but this has never been seen in nature.

Conceptual Questions

  1. Think about the drinking bird at the beginning of this section (Figure 111.1). Although the bird enjoys the theoretical maximum efficiency possible, if left to its own devices over time, the bird will cease “drinking.” What are some of the dissipative processes that might cause the bird’s motion to cease?
  2. Can improved engineering and materials be employed in heat engines to reduce heat transfer into the environment? Can they eliminate heat transfer into the environment entirely?
  3. Does the second law of thermodynamics alter the conservation of energy principle?

Problem Exercises

  1. A certain gasoline engine has an efficiency of 30.0%. What would the hot reservoir temperature be for a Carnot engine having that efficiency, if it operates with a cold reservoir temperature of [latex]2\text{00}\text{º}\text{C}[/latex]?
  2. A gas-cooled nuclear reactor operates between hot and cold reservoir temperatures of [latex]\text{700}\text{º}\text{C}[/latex] and [latex]\text{27}\text{.}0\text{º}\text{C}[/latex]. (a) What is the maximum efficiency of a heat engine operating between these temperatures? (b) Find the ratio of this efficiency to the Carnot efficiency of a standard nuclear reactor (found in Example 111.1).
  3. (a) What is the hot reservoir temperature of a Carnot engine that has an efficiency of 42.0% and a cold reservoir temperature of [latex]\text{27}\text{.}0\text{º}\text{C}[/latex]? (b) What must the hot reservoir temperature be for a real heat engine that achieves 0.700 of the maximum efficiency, but still has an efficiency of 42.0% (and a cold reservoir at [latex]\text{27}\text{.}0\text{º}\text{C}[/latex])? (c) Does your answer imply practical limits to the efficiency of car gasoline engines?
  4. Steam locomotives have an efficiency of 17.0% and operate with a hot steam temperature of [latex]\text{425}\text{º}\text{C}[/latex]. (a) What would the cold reservoir temperature be if this were a Carnot engine? (b) What would the maximum efficiency of this steam engine be if its cold reservoir temperature were [latex]\text{150}\text{º}\text{C}[/latex]?
  5. Practical steam engines utilize [latex]\text{450}\text{º}\text{C}[/latex] steam, which is later exhausted at [latex]\text{270}\text{º}\text{C}[/latex]. (a) What is the maximum efficiency that such a heat engine can have? (b) Since [latex]\text{270}\text{º}\text{C}[/latex] steam is still quite hot, a second steam engine is sometimes operated using the exhaust of the first. What is the maximum efficiency of the second engine if its exhaust has a temperature of [latex]\text{150}\text{º}\text{C}[/latex]? (c) What is the overall efficiency of the two engines? (d) Show that this is the same efficiency as a single Carnot engine operating between [latex]\text{450}\text{º}\text{C}[/latex] and [latex]\text{150}\text{º}\text{C}[/latex].
  6. A coal-fired electrical power station has an efficiency of 38%. The temperature of the steam leaving the boiler is [latex]\text{550}\text{º}\text{C}[/latex]. What percentage of the maximum efficiency does this station obtain? (Assume the temperature of the environment is [latex]\text{20}\text{º}\text{C}[/latex].)
  7. Would you be willing to financially back an inventor who is marketing a device that she claims has 25 kJ of heat transfer at 600 K, has heat transfer to the environment at 300 K, and does 12 kJ of work? Explain your answer.
  8. The heat transfer to the cold reservoir is [latex]{Q}_{\text{c}}={Q}_{\text{h}}-W=\text{25}\phantom{\rule{0.25em}{0ex}}\text{kJ}-\text{12}\phantom{\rule{0.25em}{0ex}}\text{kJ}=\text{13}\phantom{\rule{0.25em}{0ex}}\text{kJ}[/latex], so the efficiency is [latex]\mathit{Eff}=1-\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}}=1-\frac{\text{13}\phantom{\rule{0.25em}{0ex}}\text{kJ}}{\text{25}\phantom{\rule{0.25em}{0ex}}\text{kJ}}=0\text{.}\text{48}[/latex]. The Carnot efficiency is [latex]{\mathit{\text{Eff}}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}=1-\frac{\text{300}\phantom{\rule{0.25em}{0ex}}\text{K}}{\text{600}\phantom{\rule{0.25em}{0ex}}\text{K}}=0\text{.}\text{50}[/latex]. The actual efficiency is 96% of the Carnot efficiency, which is much higher than the best-ever achieved of about 70%, so her scheme is likely to be fraudulent.
  9. Unreasonable Results (a) Suppose you want to design a steam engine that has heat transfer to the environment at [latex]\text{270ºC}[/latex] and has a Carnot efficiency of 0.800. What temperature of hot steam must you use? (b) What is unreasonable about the temperature? (c) Which premise is unreasonable?
  10. Unreasonable Results Calculate the cold reservoir temperature of a steam engine that uses hot steam at [latex]\text{450}\text{º}\text{C}[/latex] and has a Carnot efficiency of 0.700. (b) What is unreasonable about the temperature? (c) Which premise is unreasonable?

Glossary

Carnot cycle
a cyclical process that uses only reversible processes, the adiabatic and isothermal processes
Carnot engine
a heat engine that uses a Carnot cycle
Carnot efficiency
the maximum theoretical efficiency for a heat engine
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book