Fluid Statics
81 Archimedes’ Principle
Learning Objectives
- Define buoyant force.
- State Archimedes’ principle.
- Explain why objects float or sink in terms of forces and fluid displacement.
- Understand the relationship between density and buoyancy.
Have you ever noticed how much heavier your arms feel when you get out of a warm bath? This sensation comes from the loss of buoyant support provided by water. But what causes this buoyant force? Why do some objects float while others sink? Do submerged objects still receive any support? Interestingly, even your body is buoyed up by air pressure, though the effect is most noticeable with objects like helium balloons (Figure 81.1).
These questions can be answered by examining how fluid pressure works. In any fluid, pressure increases with depth. As a result, the upward force acting on the bottom of an object is greater than the downward force on its top. This imbalance creates a net upward force known as the buoyant force (Figure 81.2).
The buoyant force is always present, regardless of whether an object floats, sinks, or stays suspended. If the buoyant force is greater than the object’s weight, the object rises. If it’s less, the object sinks. If it equals the object’s weight, the object remains at that depth.
Buoyant Force
The buoyant force is the net upward force exerted by a fluid on any object submerged in it.
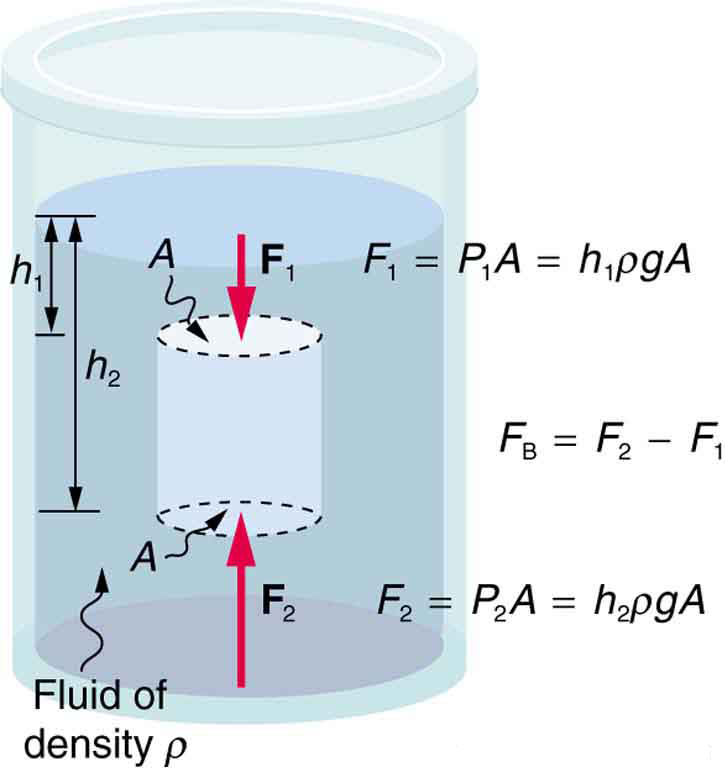
So how large is the buoyant force? When a submerged object is removed from a fluid, the fluid fills the space it occupied. The weight of the displaced fluid is equal to the buoyant force (Figure 81.3). This fundamental result is known as Archimedes’ principle.
Here, [latex]{F}_{\text{B}}[/latex] is the buoyant force and [latex]{w}_{\text{fl}}[/latex] is the weight of the displaced fluid.
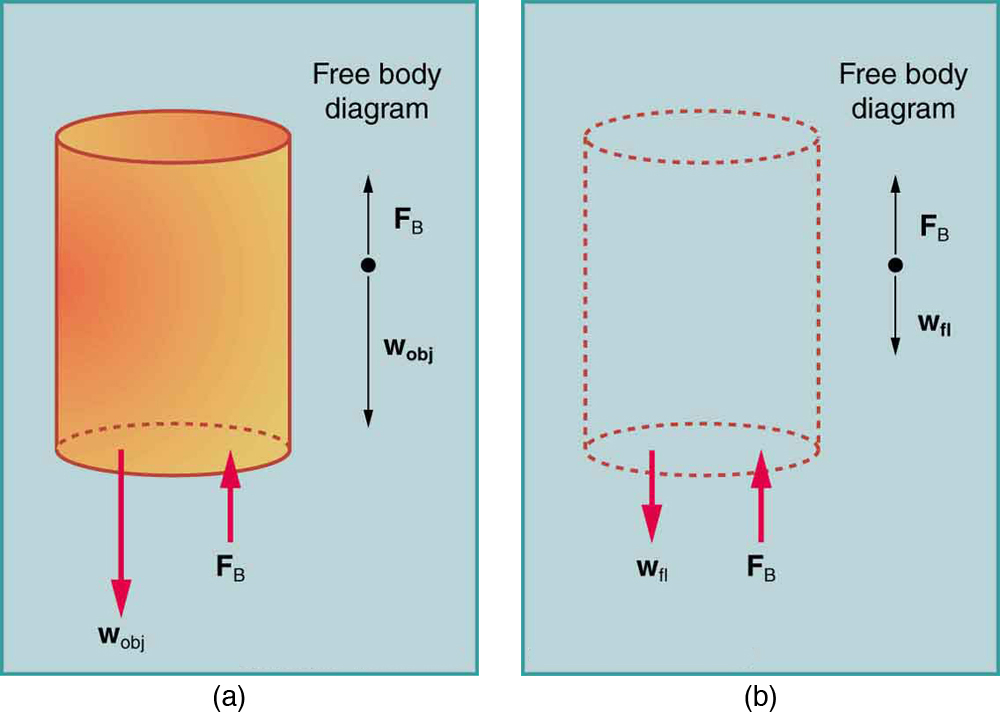
Archimedes’ Principle
The buoyant force on an object equals the weight of the fluid it displaces:
Archimedes’ principle applies to all fluids—liquids and gases—and to any object that is fully or partially submerged. This principle explains why ships made of steel can float and how fish adjust their depth in water using swim bladders. Even air exerts a buoyant force, as we see with hot air balloons and helium-filled party balloons.
Making Connections: Buoyancy and High-Tech Swimsuits
In 2008, new swimsuits were introduced for Olympic swimmers. A key requirement was that these suits could not provide a buoyancy advantage. Why? Because added buoyancy could unfairly reduce drag. How might regulators test this? One approach: check if the suit displaces more water than the swimmer’s body alone.
Take-Home Investigation
The density of aluminum is 2.7 times that of water. Take a sheet of aluminum foil, crumple it into a ball, and place it in water. Does it sink? What happens if you flatten or reshape it into a boat?
Floating and Sinking
Consider a lump of clay dropped in water—it sinks. Now mold it into the shape of a boat. It floats. Why? The boat shape displaces more water than the compact lump, which increases the buoyant force acting on it. This concept underlies the design of ships and floating medical devices like fluid-level sensors used in biomedical contexts.
Example 81.1 Calculating buoyant force: dependency on shape
(a) Calculate the buoyant force on 10,000 metric tons [latex]\left(1\text{.}\text{00}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)[/latex] of solid steel completely submerged in water, and compare this with the steel’s weight. (b) What is the maximum buoyant force that water could exert on this same steel if it were shaped into a boat that could displace [latex]1\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}[/latex] of water?
Strategy for (a)
To find the buoyant force, we must find the weight of water displaced. We can do this by using the densities of water and steel given in Table 76.1. We note that, since the steel is completely submerged, its volume and the water’s volume are the same. Once we know the volume of water, we can find its mass and weight.
Solution for (a)
First, we use the definition of density [latex]\rho =\frac{m}{V}[/latex] to find the steel’s volume, and then we substitute values for mass and density. This gives
Because the steel is completely submerged, this is also the volume of water displaced, [latex]{V}_{\text{w}}[/latex]. We can now find the mass of water displaced from the relationship between its volume and density, both of which are known. This gives
By Archimedes’ principle, the weight of water displaced is [latex]{m}_{\text{w}}g[/latex], so the buoyant force is
The steel’s weight is [latex]{m}_{\text{w}}g=9\text{.}\text{80}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex], which is much greater than the buoyant force, so the steel will remain submerged. Note that the buoyant force is rounded to two digits because the density of steel is given to only two digits.
Strategy for (b)
Here we are given the maximum volume of water the steel boat can displace. The buoyant force is the weight of this volume of water.
Solution for (b)
The mass of water displaced is found from its relationship to density and volume, both of which are known. That is,
The maximum buoyant force is the weight of this much water, or
Discussion
The maximum buoyant force is ten times the weight of the steel, meaning the ship can carry a load nine times its own weight without sinking.
Making Connections: Take-Home Investigation
A typical sheet of household aluminum foil is 0.016 mm thick. Use a piece measuring 10 cm × 15 cm. (a) What is the mass of this amount of foil? (b) If the foil is folded to form four sides, and washers or paper clips are added as cargo, what boat shape maximizes its load capacity before sinking? Test your prediction by observing which design displaces the most water without sinking.
Density and Archimedes’ Principle
Density plays a fundamental role in determining whether an object will float or sink. According to Archimedes’ principle, an object will float if its average density is less than the fluid it’s placed in. This is because the fluid, being denser, can exert a greater buoyant force—equal to the weight of the fluid displaced by the object.
Conversely, if the object’s density is greater than that of the surrounding fluid, the buoyant force is insufficient to support its weight, and it sinks. This relationship between density and buoyancy helps explain why a steel ship floats when shaped like a hull (displacing a lot of water), but sinks when shaped into a solid block.
The degree to which an object is submerged when floating depends on the ratio of its average density to the density of the fluid. This is shown in Figure 81.4, where an unloaded ship floats higher than a loaded ship because the total density of the ship + cargo system increases, displacing more water.
Here, [latex]V_{\text{sub}}[/latex] is the volume submerged (equal to the volume of displaced fluid [latex]V_{\text{fl}}[/latex]), and [latex]V_{\text{obj}}[/latex] is the total volume of the object.
By applying [latex]\rho = \frac{m}{V}[/latex], we can relate this to density:
Since the mass of the fluid displaced equals the object’s mass when floating, the masses cancel out, resulting in:
Thus, the proportion of the object submerged is equal to the ratio of its density to that of the fluid. This is useful in various applications—for example, measuring the fat content of the human body using water displacement or floating devices.
To further quantify buoyancy, we use the concept of specific gravity, which is the ratio of a substance’s density to that of water:
Here, [latex]\bar{\rho}[/latex] is the average density of the object and [latex]\rho_{\text{w}}[/latex] is the density of water at 4°C (approximately 1000 kg/m³). Specific gravity is dimensionless and often used in medicine, geology, and chemistry. For example, urine’s specific gravity is used in clinical diagnostics to assess hydration or kidney function.
Specific Gravity
Specific gravity is the ratio of an object’s average density to that of water. If it’s less than 1, the object floats. If greater than 1, it sinks. Specific gravity = 1 means the object remains neutrally buoyant, suspended in the fluid. This is desirable for scuba divers who aim to hover in water without floating up or sinking down.
Making Connections: Take-Home Investigation
A typical sheet of household aluminum foil is 0.016 mm thick. Use a piece measuring 10 cm × 15 cm. (a) What is the mass of this amount of foil? (b) If the foil is folded to form four sides, and washers or paper clips are added as cargo, what boat shape maximizes its load capacity before sinking? Test your prediction by observing which design displaces the most water without sinking.
Density and Archimedes’ Principle
Density plays a fundamental role in determining whether an object will float or sink. According to Archimedes’ principle, an object will float if its average density is less than the fluid it’s placed in. This is because the fluid, being denser, can exert a greater buoyant force—equal to the weight of the fluid displaced by the object.
Conversely, if the object’s density is greater than that of the surrounding fluid, the buoyant force is insufficient to support its weight, and it sinks. This relationship between density and buoyancy helps explain why a steel ship floats when shaped like a hull (displacing a lot of water), but sinks when shaped into a solid block.
The degree to which an object is submerged when floating depends on the ratio of its average density to the density of the fluid. This is shown in Figure 81.4, where an unloaded ship floats higher than a loaded ship because the total density of the ship + cargo system increases, displacing more water.
Here, [latex]V_{\text{sub}}[/latex] is the volume submerged (equal to the volume of displaced fluid [latex]V_{\text{fl}}[/latex]), and [latex]V_{\text{obj}}[/latex] is the total volume of the object.
By applying [latex]\rho = \frac{m}{V}[/latex], we can relate this to density:
Since the mass of the fluid displaced equals the object’s mass when floating, the masses cancel out, resulting in:
Thus, the proportion of the object submerged is equal to the ratio of its density to that of the fluid. This is useful in various applications—for example, measuring the fat content of the human body using water displacement or floating devices.
To further quantify buoyancy, we use the concept of specific gravity, which is the ratio of a substance’s density to that of water:
Here, [latex]\bar{\rho}[/latex] is the average density of the object and [latex]\rho_{\text{w}}[/latex] is the density of water at 4°C (approximately 1000 kg/m³). Specific gravity is dimensionless and often used in medicine, geology, and chemistry. For example, urine’s specific gravity is used in clinical diagnostics to assess hydration or kidney function.
Specific Gravity
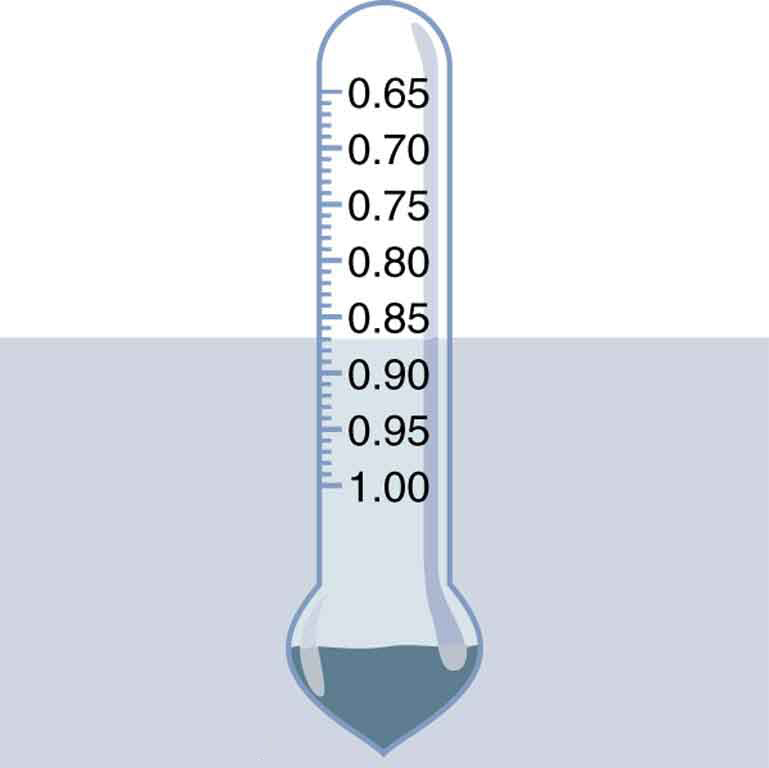
Specific gravity is the ratio of an object’s average density to that of water. It can be measured with a hydrometer like the one inf Figure 81.5. If it’s less than 1, the object floats. If greater than 1, it sinks. Specific gravity = 1 means the object remains neutrally buoyant, suspended in the fluid. This is desirable for scuba divers who aim to hover in water without floating up or sinking down.
Figure 81.2 Calculating Average Density: Floating Woman
Suppose a 60.0-kg woman floats in freshwater with [latex]97.0%[/latex] of her volume submerged when her lungs are full of air. What is her average density?
Strategy
We can find the woman’s density by solving the equation
for the density of the object. This yields
We know both the fraction submerged and the density of water, and so we can calculate the woman’s density.
Solution
Entering the known values into the expression for her density, we obtain
Discussion
Her density is less than the fluid density. We expect this because she floats. Body density is one indicator of a person’s percent body fat, of interest in medical diagnostics and athletic training. (See Figure 81.6.)
Applications of Density and Buoyancy in the Real World
Many common phenomena demonstrate how lower-density substances float in higher-density fluids. For example, oil floats on water, cork floats in wine, and hot wax rises in a lava lamp due to temperature-induced density changes. These examples reflect a key principle in fluid mechanics: buoyant force acts in proportion to the weight of the fluid displaced.
Even more remarkable is how this principle applies to Earth systems. For instance, magma rises in a volcano because molten rock is less dense than the solid crust above it. Similarly, entire mountain ranges “float” on the denser mantle below—an application of buoyant force on a geologic scale. These insights help geologists understand tectonic movement and crustal dynamics. Although we often consider the Earth to be solid, it behaves like a fluid under long time scales and pressure.
More Density Measurements
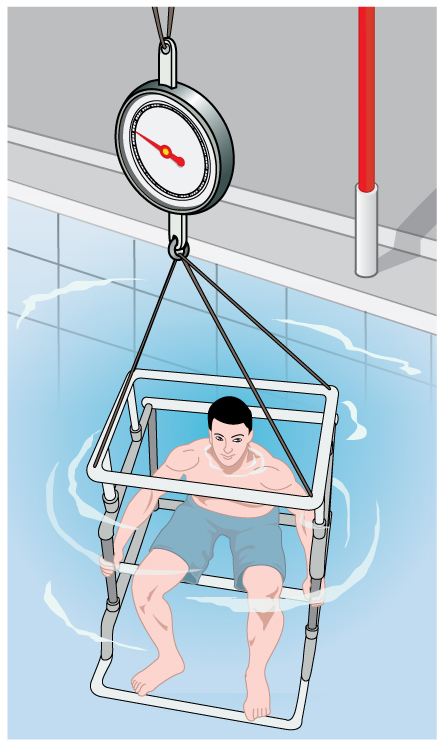
One widely used method for determining density relies on Archimedes’ principle, as illustrated in Figure 81.7. This technique is applicable in laboratory medicine, forensic science, and materials testing.
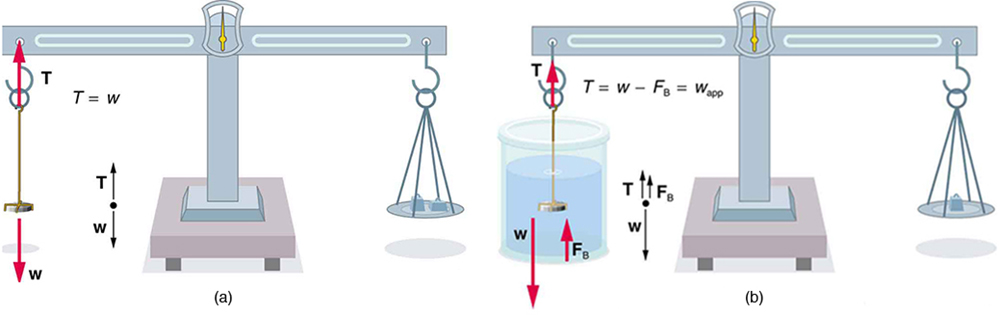
To apply this method, the object is first weighed in air and then again while submerged in a fluid of known density. The submerged weight appears to be less than the weight in air due to the buoyant force. This is called the object’s apparent weight. The difference between the actual weight and the apparent weight is equal to the weight of the fluid displaced.
On scales that measure mass instead of weight (such as laboratory balances), this same concept applies as an apparent mass loss:
This method is not only valuable in physics labs, but also in health professions. For example, body composition testing using water displacement (hydrostatic weighing) relies on the same principle to determine body density and estimate fat content—important for monitoring athletic performance and metabolic health.
The next example illustrates the use of this technique.
Example 81.3 Calculating Density: Is the Coin Authentic?
The mass of an ancient Greek coin is determined in air to be 8.630 g. When the coin is submerged in water as shown in Figure 81.7, its apparent mass is 7.800 g. Calculate its density, given that water has a density of [latex]1\text{.}\text{000}\phantom{\rule{0.25em}{0ex}}{\text{g/cm}}^{3}[/latex] and that effects caused by the wire suspending the coin are negligible.
Strategy
To calculate the coin’s density, we need its mass (which is given) and its volume. The volume of the coin equals the volume of water displaced. The volume of water displaced [latex]{V}_{\text{w}}[/latex] can be found by solving the equation for density [latex]\rho =\frac{m}{V}[/latex] for [latex]V[/latex].
Solution
The volume of water is [latex]{V}_{\text{w}}=\frac{{m}_{\text{w}}}{{\rho }_{\text{w}}}[/latex] where [latex]{m}_{\text{w}}[/latex] is the mass of water displaced. As noted, the mass of the water displaced equals the apparent mass loss, which is [latex]{m}_{\text{w}}=8\text{.}\text{630 g}-7\text{.}\text{800 g}=0\text{.}\text{830 g}[/latex]. Thus the volume of water is [latex]{V}_{\text{w}}=\frac{0\text{.}\text{830 g}}{1\text{.}\text{000 g}{\text{/cm}}^{3}}=0\text{.}\text{830}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}[/latex]. This is also the volume of the coin, since it is completely submerged. We can now find the density of the coin using the definition of density:
Discussion
You can see from Density Table 76.1 that this density is very close to that of pure silver, appropriate for this type of ancient coin. Most modern counterfeits are not pure silver.
The Story Behind Archimedes’ Principle
The development of Archimedes’ principle is linked to a classic tale from ancient Greece that illustrates the ingenuity of early scientific thought. The king of Syracuse once commissioned a crown and suspected that it had been adulterated with cheaper metals. Because gold maintains its bright yellow appearance even when mixed with other metals, visual inspection could not confirm its purity. Analytical chemistry had not yet been invented, but Archimedes knew that gold has a uniquely high density—higher than any other known metal of the time.
According to legend, while taking a bath, Archimedes observed how water buoyed his body. This led him to realize that an object’s volume—and thus its density—could be determined by how much fluid it displaced. Excited by this insight, he reportedly ran through the streets shouting “Eureka!”—Greek for “I have found it.” Whether or not this tale is historically accurate, the principle that bears his name remains fundamental to fluid mechanics and continues to inform modern science, medicine, and engineering.
Section Summary
- Buoyant force is the net upward force on any object in any fluid. If the buoyant force is greater than the object’s weight, the object floats. If it is less, the object sinks. If the buoyant force equals the object’s weight, the object remains suspended. The buoyant force acts in all cases.
- Archimedes’ principle states that the buoyant force on an object equals the weight of the fluid it displaces. This applies to objects that are partially or fully submerged in a fluid.
- Specific gravity is the ratio of an object’s average density to the density of a fluid (typically water). Specific gravity is dimensionless and helps predict whether an object will float or sink.
Conceptual Questions
- More force is required to pull the plug in a full bathtub than when it is empty. Does this contradict Archimedes’ principle? Explain your answer.
- Do fluids exert buoyant forces in a “weightless” environment, such as in the space shuttle? Explain your answer.
- Will the same ship float higher in salt water than in freshwater? Explain your answer.
- Marbles dropped into a partially filled bathtub sink to the bottom. Part of their weight is supported by buoyant force, yet the downward force on the bottom of the tub increases by exactly the weight of the marbles. Explain why.
Problem Exercises
- What fraction of ice is submerged when it floats in freshwater, given the density of water at 0°C is very close to [latex]\text{1000 kg}{\text{/m}}^{3}[/latex]?
- Logs sometimes float vertically in a lake because one end has become water-logged and denser than the other. What is the average density of a uniform-diameter log that floats with [latex]20.0%[/latex] of its length above water?
- Find the density of a fluid in which a hydrometer having a density of [latex]0\text{.}\text{750 g}\text{/mL}[/latex] floats with [latex]\text{92.0%}[/latex] of its volume submerged.
- If your body has a density of [latex]\text{995 kg}{\text{/m}}^{3}[/latex], what fraction of you will be submerged when floating gently in: (a) Freshwater? (b) Salt water, which has a density of [latex]\text{1027 kg}{\text{/m}}^{3}[/latex]?
- Bird bones have air pockets in them to reduce their weight—this also gives them an average density significantly less than that of the bones of other animals. Suppose an ornithologist weighs a bird bone in air and in water and finds its mass is [latex]\text{45.0 g}[/latex] and its apparent mass when submerged is [latex]3.60 g[/latex] (the bone is watertight). (a) What mass of water is displaced? (b) What is the volume of the bone? (c) What is its average density?
- A rock with a mass of 540 g in air is found to have an apparent mass of 342 g when submerged in water. (a) What mass of water is displaced? (b) What is the volume of the rock? (c) What is its average density? Is this consistent with the value for granite?
- Archimedes’ principle can be used to calculate the density of a fluid as well as that of a solid. Suppose a chunk of iron with a mass of 390.0 g in air is found to have an apparent mass of 350.5 g when completely submerged in an unknown liquid. (a) What mass of fluid does the iron displace? (b) What is the volume of iron, using its density as given in Density table 76.1(c) Calculate the fluid’s density and identify it.
- In an immersion measurement of a woman’s density, she is found to have a mass of 62.0 kg in air and an apparent mass of 0.0850 kg when completely submerged with lungs empty. (a) What mass of water does she displace? (b) What is her volume? (c) Calculate her density. (d) If her lung capacity is 1.75 L, is she able to float without treading water with her lungs filled with air?
- Some fish have a density slightly less than that of water and must exert a force (swim) to stay submerged. What force must an 85.0-kg grouper exert to stay submerged in salt water if its body density is [latex]\text{1015}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}[/latex]?
- (a) Calculate the buoyant force on a 2.00-L helium balloon. (b) Given the mass of the rubber in the balloon is 1.50 g, what is the net vertical force on the balloon if it is let go? You can neglect the volume of the rubber.
- (a) What is the density of a woman who floats in freshwater with [latex]4.00%[/latex] of her volume above the surface? This could be measured by placing her in a tank with marks on the side to measure how much water she displaces when floating and when held under water (briefly). (b) What percent of her volume is above the surface when she floats in seawater?
- A certain man has a mass of 80 kg and a density of [latex]\text{955}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}[/latex] (excluding the air in his lungs). (a) Calculate his volume. (b) Find the buoyant force air exerts on him. (c) What is the ratio of the buoyant force to his weight?
- A simple compass can be made by placing a small bar magnet on a cork floating in water. (a) What fraction of a plain cork will be submerged when floating in water? (b) If the cork has a mass of 10.0 g and a 20.0-g magnet is placed on it, what fraction of the cork will be submerged? (c) Will the bar magnet and cork float in ethyl alcohol?
- What fraction of an iron anchor’s weight will be supported by buoyant force when submerged in saltwater?
- Scurrilous con artists have been known to represent gold-plated tungsten ingots as pure gold and sell them to the greedy at prices much below gold value but deservedly far above the cost of tungsten. With what accuracy must you be able to measure the mass of such an ingot in and out of water to tell that it is almost pure tungsten rather than pure gold?
- A twin-sized air mattress used for camping has dimensions of 100 cm by 200 cm by 15 cm when blown up. The weight of the mattress is 2 kg. How heavy a person could the air mattress hold if it is placed in freshwater?
- Referring to Figure 81.3, prove that the buoyant force on the cylinder is equal to the weight of the fluid displaced (Archimedes’ principle). You may assume that the buoyant force is [latex]{F}_{2}-{F}_{1}[/latex] and that the ends of the cylinder have equal areas [latex]A[/latex]. Note that the volume of the cylinder (and that of the fluid it displaces) equals [latex]\left({h}_{2}-{h}_{1}\right)A[/latex].
- (a) A 75.0-kg man floats in freshwater with [latex]3.00%[/latex] of his volume above water when his lungs are empty, and [latex]5.00%[/latex] of his volume above water when his lungs are full. Calculate the volume of air he inhales—called his lung capacity—in liters. (b) Does this lung volume seem reasonable?
Glossary
- Archimedes’ principle
- the buoyant force on an object equals the weight of the fluid it displaces
- buoyant force
- the net upward force on any object in any fluid
- specific gravity
- the ratio of the density of an object to a fluid (usually water)
Learning Objectives
- Restate Maxwell’s equations.
The Scotsman James Clerk Maxwell (1831–1879) is regarded as the greatest theoretical physicist of the 19th century. (See (Figure).) Although he died young, Maxwell not only formulated a complete electromagnetic theory, represented by Maxwell’s equations, he also developed the kinetic theory of gases and made significant contributions to the understanding of color vision and the nature of Saturn’s rings.
Maxwell brought together all the work that had been done by brilliant physicists such as Oersted, Coulomb, Gauss, and Faraday, and added his own insights to develop the overarching theory of electromagnetism. Maxwell’s equations are paraphrased here in words because their mathematical statement is beyond the level of this text. However, the equations illustrate how apparently simple mathematical statements can elegantly unite and express a multitude of concepts—why mathematics is the language of science.
- Electric field lines originate on positive charges and terminate on negative charges. The electric field is defined as the force per unit charge on a test charge, and the strength of the force is related to the electric constant [latex]{\epsilon }_{0}[/latex], also known as the permittivity of free space. From Maxwell’s first equation we obtain a special form of Coulomb’s law known as Gauss’s law for electricity.
- Magnetic field lines are continuous, having no beginning or end. No magnetic monopoles are known to exist. The strength of the magnetic force is related to the magnetic constant [latex]{\mu }_{0}[/latex], also known as the permeability of free space. This second of Maxwell’s equations is known as Gauss’s law for magnetism.
- A changing magnetic field induces an electromotive force (emf) and, hence, an electric field. The direction of the emf opposes the change. This third of Maxwell’s equations is Faraday’s law of induction, and includes Lenz’s law.
- Magnetic fields are generated by moving charges or by changing electric fields. This fourth of Maxwell’s equations encompasses Ampere’s law and adds another source of magnetism—changing electric fields.
Maxwell’s equations encompass the major laws of electricity and magnetism. What is not so apparent is the symmetry that Maxwell introduced in his mathematical framework. Especially important is his addition of the hypothesis that changing electric fields create magnetic fields. This is exactly analogous (and symmetric) to Faraday’s law of induction and had been suspected for some time, but fits beautifully into Maxwell’s equations.
Symmetry is apparent in nature in a wide range of situations. In contemporary research, symmetry plays a major part in the search for sub-atomic particles using massive multinational particle accelerators such as the new Large Hadron Collider at CERN.
Maxwell’s complete and symmetric theory showed that electric and magnetic forces are not separate, but different manifestations of the same thing—the electromagnetic force. This classical unification of forces is one motivation for current attempts to unify the four basic forces in nature—the gravitational, electrical, strong, and weak nuclear forces.
Since changing electric fields create relatively weak magnetic fields, they could not be easily detected at the time of Maxwell’s hypothesis. Maxwell realized, however, that oscillating charges, like those in AC circuits, produce changing electric fields. He predicted that these changing fields would propagate from the source like waves generated on a lake by a jumping fish.
The waves predicted by Maxwell would consist of oscillating electric and magnetic fields—defined to be an electromagnetic wave (EM wave). Electromagnetic waves would be capable of exerting forces on charges great distances from their source, and they might thus be detectable. Maxwell calculated that electromagnetic waves would propagate at a speed given by the equation
When the values for [latex]{\mu }_{0}[/latex] and [latex]{\epsilon }_{0}[/latex] are entered into the equation for [latex]c[/latex], we find that
which is the speed of light. In fact, Maxwell concluded that light is an electromagnetic wave having such wavelengths that it can be detected by the eye.
Other wavelengths should exist—it remained to be seen if they did. If so, Maxwell’s theory and remarkable predictions would be verified, the greatest triumph of physics since Newton. Experimental verification came within a few years, but not before Maxwell’s death.
Hertz’s Observations
The German physicist Heinrich Hertz (1857–1894) was the first to generate and detect certain types of electromagnetic waves in the laboratory. Starting in 1887, he performed a series of experiments that not only confirmed the existence of electromagnetic waves, but also verified that they travel at the speed of light.
Hertz used an AC [latex]\text{RLC}[/latex] (resistor-inductor-capacitor) circuit that resonates at a known frequency [latex]{f}_{0}=\frac{1}{2\pi \sqrt{\text{LC}}}[/latex] and connected it to a loop of wire as shown in (Figure). High voltages induced across the gap in the loop produced sparks that were visible evidence of the current in the circuit and that helped generate electromagnetic waves.
Across the laboratory, Hertz had another loop attached to another [latex]\text{RLC}[/latex] circuit, which could be tuned (as the dial on a radio) to the same resonant frequency as the first and could, thus, be made to receive electromagnetic waves. This loop also had a gap across which sparks were generated, giving solid evidence that electromagnetic waves had been received.
Hertz also studied the reflection, refraction, and interference patterns of the electromagnetic waves he generated, verifying their wave character. He was able to determine wavelength from the interference patterns, and knowing their frequency, he could calculate the propagation speed using the equation [latex]\upsilon =\mathrm{f\lambda }[/latex] (velocity—or speed—equals frequency times wavelength). Hertz was thus able to prove that electromagnetic waves travel at the speed of light. The SI unit for frequency, the hertz ([latex]1 Hz=\text{1 cycle/sec}[/latex]), is named in his honor.
Section Summary
- Electromagnetic waves consist of oscillating electric and magnetic fields and propagate at the speed of light [latex]c[/latex]. They were predicted by Maxwell, who also showed that
[latex]c=\frac{1}{\sqrt{{\mu }_{0}{\epsilon }_{0}}},[/latex]
where [latex]{\mu }_{0}[/latex] is the permeability of free space and [latex]{\epsilon }_{0}[/latex] is the permittivity of free space.
- Maxwell’s prediction of electromagnetic waves resulted from his formulation of a complete and symmetric theory of electricity and magnetism, known as Maxwell’s equations.
- These four equations are paraphrased in this text, rather than presented numerically, and encompass the major laws of electricity and magnetism. First is Gauss’s law for electricity, second is Gauss’s law for magnetism, third is Faraday’s law of induction, including Lenz’s law, and fourth is Ampere’s law in a symmetric formulation that adds another source of magnetism—changing electric fields.
Problems & Exercises
Verify that the correct value for the speed of light [latex]c[/latex] is obtained when numerical values for the permeability and permittivity of free space ([latex]{\mu }_{0}[/latex] and [latex]{\epsilon }_{0}[/latex]) are entered into the equation [latex]c=\frac{1}{\sqrt{{\mu }_{0}{\epsilon }_{0}}}[/latex].
Show that, when SI units for [latex]{\mu }_{0}[/latex] and [latex]{\epsilon }_{0}[/latex] are entered, the units given by the right-hand side of the equation in the problem above are m/s.
Glossary
- electromagnetic waves
- radiation in the form of waves of electric and magnetic energy
- Maxwell’s equations
- a set of four equations that comprise a complete, overarching theory of electromagnetism
- RLC circuit
- an electric circuit that includes a resistor, capacitor and inductor
- hertz
- an SI unit denoting the frequency of an electromagnetic wave, in cycles per second
- speed of light
- in a vacuum, such as space, the speed of light is a constant 3 x 108 m/s
- electromotive force (emf)
- energy produced per unit charge, drawn from a source that produces an electrical current
- electric field lines
- a pattern of imaginary lines that extend between an electric source and charged objects in the surrounding area, with arrows pointed away from positively charged objects and toward negatively charged objects. The more lines in the pattern, the stronger the electric field in that region
- magnetic field lines
- a pattern of continuous, imaginary lines that emerge from and enter into opposite magnetic poles. The density of the lines indicates the magnitude of the magnetic field
the buoyant force on an object equals the weight of the fluid it displaces
the net upward force on any object in any fluid
the ratio of the density of an object to a fluid (usually water)
