"

Thermodynamics

112 Applications of Thermodynamics: Heat Pumps and Refrigerators

Learning Objectives

  • Describe how heat engines operate as heat pumps and refrigerators.
  • Explain how a heat pump transfers thermal energy into an interior space.
  • Distinguish between the function of heat pumps and refrigerators.
  • Calculate the coefficient of performance (COP) of a heat pump.
Photograph of various expensive refrigerators displayed in a home appliance store.
Figure 112.1: While most people associate refrigerators with keeping food cold, they are also heat pumps. They operate by transferring heat from a cooler interior to the warmer air outside. (credit: Id1337x, Wikimedia Commons)

Heat pumps, refrigerators, and air conditioners all perform the same basic task: they transfer heat from a cooler region to a warmer one. This is the reverse of what a standard heat engine does. Because this action goes against the natural direction of heat flow, it requires a work input [latex]W[/latex]. The total heat delivered to the warmer reservoir is therefore the sum of the heat removed from the cold reservoir and the work added:

[latex]Q_{\text{h}} = Q_{\text{c}} + W[/latex]

Here, [latex]Q_{\text{c}}[/latex] is the heat extracted from the cold region (e.g., outside air or inside a fridge), and [latex]Q_{\text{h}}[/latex] is the heat delivered to the warm region (e.g., your home or the external environment). The sign convention assumes all values are positive, and directionality is indicated by schematic diagrams, not by signs.

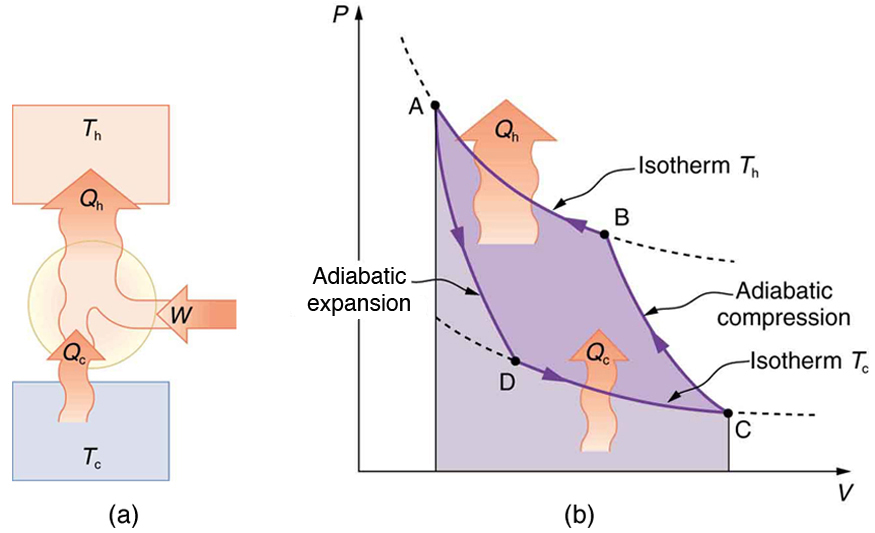
Part a of the figure shows a heat pump, drawn as a circle. Work W, indicated by a bold orange arrow, is put in to to the pump to transfer heat Q sub c, indicated by a bold orange arrow, out of a cold temperature reservoir T sub c, drawn as a blue rectangle, and pumps heat Q sub h, indicated by a larger bold orange arrow, into high temperature reservoir T sub h. Part b of the figure shows a P V diagram for a Carnot cycle. The pressure P is along the Y axis and the volume V is along the X axis. The graph shows a complete cycle A D C B A. The path begins at point A, then it drops sharply down and slightly to the right until point D. This is marked as an adiabatic expansion. Then the curve drops down more gradually, still to the right, from point D to point C. This is marked as an isotherm at temperature T sub c, during which heat Q sub c enters the system. The curve then rises from point C to point B along the direction opposite to that of A D. This is an adiabatic compression. The last part of the curve rises up from point B back to A. This is marked as an isotherm at temperature T sub h, during which heat Q sub h leaves the system. The path D C is lower than path B A. Heat entering and leaving the system is indicated by bold orange arrows, with Q sub h larger than Q sub c.
Figure 112.2:(a) A heat pump transfers heat from a cold reservoir at temperature [latex]T_{\text{c}}[/latex] to a hot reservoir at [latex]T_{\text{h}}[/latex], requiring work input [latex]W[/latex]. (b) The Carnot cycle on a [latex]PV[/latex] diagram shows the reversed paths of heat transfer and work. The area enclosed by the cycle is negative, indicating net work input.

Heat Pumps in Heating Mode

Heat pumps are widely used for home heating. Their main advantage over direct fuel combustion is efficiency: rather than converting all input energy into heat, heat pumps extract free energy in the form of thermal energy from the outside air—even when it’s below freezing. You only pay for the electrical energy used to compress the refrigerant, but you receive both this energy and the absorbed environmental heat into your home.

In many cases, a well-functioning heat pump can transfer two to three times as much thermal energy into the home as the electrical energy it consumes. However, if electricity is expensive or the outside air is extremely cold, operating costs can exceed those of simple fuel-based heating.

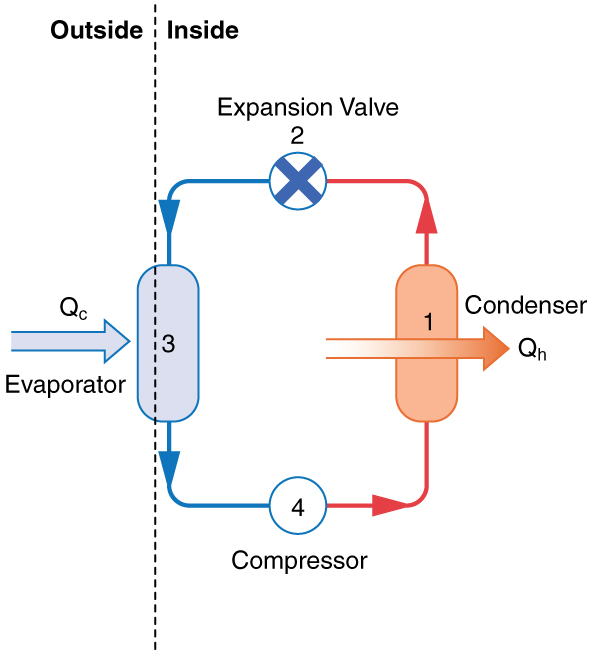
The diagram shows a diagram of a heat pump. There are four components connected by pipes. They are a condenser (1), an expansion valve (2), an evaporator (3), and a compressor (4), connected in that order. The evaporator coils are outside; all of the other components are inside. Heat Q sub c is absorbed from the outside air at the evaporator, and heat Q sub h is emitted inside from the condenser.
Figure 112.3: The basic components of a heat pump include: (1) condenser, (2) expansion valve, (3) evaporator, and (4) compressor. In heating mode, heat is absorbed from the outside air at the evaporator, compressed, and then transferred into the indoor air at the condenser.

The working fluid (a refrigerant) absorbs heat in the outdoor evaporator coils and evaporates into a gas. The compressor then performs work [latex]W[/latex] on the gas, increasing its temperature and pressure. This hot gas enters the condenser coils inside the home, where it releases heat to the room as it condenses back into a liquid. The liquid refrigerant is cooled and depressurized by passing through the expansion valve and returns to the evaporator to begin the cycle again.

Coefficient of Performance (COP)

The effectiveness of a heat pump is measured by its coefficient of performance, or [latex]\text{COP}_{\text{hp}}[/latex]. This is the ratio of the heat delivered to the heated space to the work input required:

[latex]\text{COP}_{\text{hp}} = \frac{Q_{\text{h}}}{W}[/latex]

In contrast, a heat engine’s efficiency is given by:

[latex]\text{Eff} = \frac{W}{Q_{\text{h}}}[/latex]

These expressions are reciprocals of each other, implying:

[latex]\text{COP}_{\text{hp}} = \frac{1}{\text{Eff}}[/latex]

Since no heat engine is 100% efficient, [latex]\text{COP}_{\text{hp}}[/latex] is always greater than 1. This means that a properly functioning heat pump delivers more heat energy than the electrical work it consumes.

From the Carnot efficiency, we know:

[latex]\text{Eff}_{\text{C}} = 1 - \frac{T_{\text{c}}}{T_{\text{h}}}[/latex]

So, for a Carnot heat pump, we find:

[latex]\text{COP}_{\text{hp}} = \frac{1}{1 - \frac{T_{\text{c}}}{T_{\text{h}}}}[/latex]

Thus, heat pumps perform best when the temperature difference between inside and outside is small. In very cold climates, their efficiency drops because extracting thermal energy from cold air becomes more difficult.

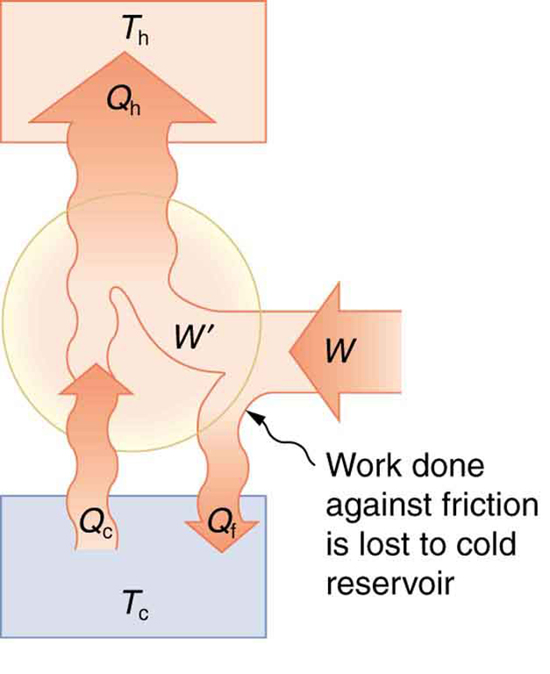
A diagram of a heat pump (shown as a circle). Work W, indicated by a large, wavy orange arrow, is the total work put into the pump. Part of this work is done against friction and is lost in the form of frictional heat, Q sub f, to the cold reservoir. The portion of work that is used by the heat pump is represented by W prime. The pump transfers heat Q sub h, indicated by a large orange arrow, into the hot reservoir, a tan-colored rectangle, at temperature T sub h. Frictional heat Q sub f, indicated by a wavy orange arrow, is transferred to the cold reservoir, a blue rectangle at temperature T sub c. Heat Q sub c, indicated by a smaller wavy orange arrow, is transferred into the pump from the cold reservoir. Heat Q sub h is formed from a combination of W prime and Q sub c.
Figure 112.4: Real-world heat pumps are affected by friction and other inefficiencies. Some of the work input [latex]W[/latex] is lost as heat [latex]Q_f[/latex] before reaching the compressor. Only the remaining portion [latex]W'[/latex] contributes to the actual heat transfer. This reduces the system’s coefficient of performance.

Irreversible processes such as friction reduce the system’s performance, converting useful work into waste heat before it reaches the compressor. Therefore, minimizing these losses is key to achieving high efficiency in heating and cooling systems.

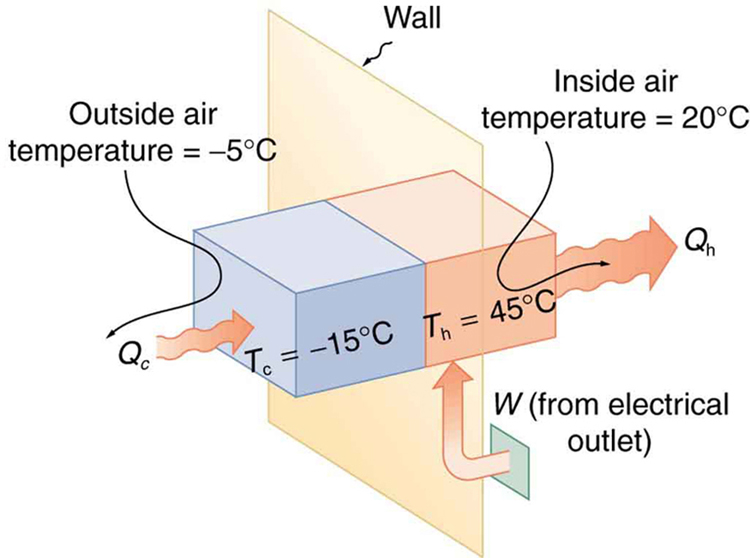
Example 112.1 The Best COP hp of a Heat Pump for Home Use

A heat pump used to warm a home must employ a cycle that produces a working fluid at temperatures greater than typical indoor temperature so that heat transfer to the inside can take place. Similarly, it must produce a working fluid at temperatures that are colder than the outdoor temperature so that heat transfer occurs from outside. Its hot and cold reservoir temperatures therefore cannot be too close, placing a limit on its [latex]{\text{COP}}_{\text{hp}}[/latex]. (See Figure 112.5.) What is the best coefficient of performance possible for such a heat pump, if it has a hot reservoir temperature of [latex]\text{45}\text{.}0\text{º}\text{C}[/latex] and a cold reservoir temperature of [latex]-\text{15}\text{.}0\text{º}\text{C}[/latex]?

Strategy

A Carnot engine reversed will give the best possible performance as a heat pump. As noted above, [latex]{\text{COP}}_{\text{hp}}=1/\text{Eff}[/latex], so that we need to first calculate the Carnot efficiency to solve this problem.

Solution

Carnot efficiency in terms of absolute temperature is given by:

[latex]{\text{Eff}}_{\text{C}}=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}\text{.}[/latex]

The temperatures in kelvins are [latex]{T}_{\text{h}}=\text{318 K}[/latex] and [latex]{T}_{\text{c}}=\text{258 K}[/latex], so that

[latex]{\text{Eff}}_{\text{C}}=1-\frac{\text{258 K}}{\text{318 K}}=0\text{.}\text{1887}\text{.}[/latex]

Thus, from the discussion above,

[latex]{\text{COP}}_{\text{hp}}=\frac{1}{\text{Eff}}=\frac{1}{0\text{.}\text{1887}}=5\text{.}\text{30},[/latex]

or

[latex]{\text{COP}}_{\text{hp}}=\frac{{Q}_{\text{h}}}{W}=5\text{.}\text{30}\text{,}[/latex]

so that

[latex]{Q}_{\text{h}}=5.30 W\text{.}[/latex]

Discussion

This result means that the heat transfer by the heat pump is 5.30 times as much as the work put into it. It would cost 5.30 times as much for the same heat transfer by an electric room heater as it does for that produced by this heat pump. This is not a violation of conservation of energy. Cold ambient air provides 4.3 J per 1 J of work from the electrical outlet.

The figure shows a schematic diagram of a heat pump. The hot and cold reservoirs are shown as two rectangular boxes attached to a vertical rectangular wall. The hot reservoir is at temperature T sub c equals negative fifteen degrees Celsius and the hot reservoir is at a temperature T sub h equals forty five degrees Celsius. Work W is shown to enter from an electrical outlet. Heat Q sub c is shown to enter the cold reservoir at an outside air temperature of negative five degrees Celsius and Q sub h is shown to leave the hot reservoir at an inside air temperature of twenty degrees Celsius.
Figure 112.5: Heat transfer from the outside to the inside, along with work done to run the pump, takes place in the heat pump of the example above. Note that the cold temperature produced by the heat pump is lower than the outside temperature, so that heat transfer into the working fluid occurs. The pump’s compressor produces a temperature greater than the indoor temperature in order for heat transfer into the house to occur.

In the real world, heat pumps are not as efficient as ideal theoretical models. For most commercially available systems, the coefficient of performance ([latex]{\text{COP}}_{\text{hp}}[/latex]) typically ranges from 2 to 4. This means the heat delivered to the warm space is 2 to 4 times greater than the work input [latex]W[/latex].

Despite this high ratio, the economic feasibility of heat pumps depends on several factors. The electricity that powers the compressor is often more expensive per unit of energy than natural gas or other fuels. Additionally, the initial purchase and installation cost of a heat pump is generally higher than that of a traditional furnace. This means the system must operate for several years before the savings on energy bills outweigh the higher upfront cost.

Heat pumps are most economical in regions with mild winters and moderate summers—especially where electricity is inexpensive and fuel costs are high. Another benefit is that the same unit can provide cooling in the summer, making it a convenient all-in-one system. These dual-function units are often referred to as reverse-cycle systems or split-system coolers, as shown in Figure 112.6.

A residential heat pump.
Figure 112.6: Heat pumps can reverse the flow of the working fluid to switch between heating and cooling. In warm weather, heat is transferred from inside the home to the outside air. In cold weather, heat is absorbed from the outside air and transferred into the home.

Air Conditioners and Refrigerators

Air conditioners and refrigerators are specialized types of heat pumps designed specifically for cooling. Like heat pumps, they require work input to transfer heat from a colder interior space to a warmer external environment. This energy cost is often what limits their long-term efficiency.

The performance of air conditioners and refrigerators is evaluated using a similar concept to that used with heat pumps. Instead of focusing on heat delivered to a warm space, we measure how much heat [latex]{Q}_{\text{c}}[/latex] is removed from the cold space per unit of work input [latex]W[/latex]. This gives us the coefficient of performance for refrigerators:

[latex]{\text{COP}}_{\text{ref}} = \frac{Q_{\text{c}}}{W}[/latex]

Since [latex]Q_{\text{h}} = Q_{\text{c}} + W[/latex], and because [latex]Q_{\text{h}} > Q_{\text{c}}[/latex], the coefficient of performance for a heat pump is always greater than that for a refrigerator operating between the same two temperatures. In fact, it can be shown that:

[latex]{\text{COP}}_{\text{ref}} = {\text{COP}}_{\text{hp}} - 1[/latex]

This equation reveals that a refrigerator is slightly less effective than a heat pump at transferring energy because it defines useful energy differently—what is useful in one case is considered waste in the other.

Despite this, modern refrigerators and air conditioners often have [latex]{\text{COP}}_{\text{ref}}[/latex] values between 2 and 6, which is very good. These values are still below the idealized Carnot efficiency, due to real-world losses like friction and imperfect heat exchange.

Energy Efficiency Ratings (EER)

To help consumers make informed decisions, many countries have developed rating systems for cooling appliances. One of the most common is the Energy Efficiency Ratio (EER), which compares cooling capacity to electrical power input. Although it uses non-SI units, the EER is a convenient benchmark when comparing different models. Appliances with a higher EER cost less to operate but usually come with a higher purchase price.

In Australia, Canada, New Zealand, and the United States, the EER is often displayed using a 5-star rating system. More stars indicate greater energy efficiency and lower long-term cost.

The EER is defined as:

[latex]\text{EER} = \frac{Q_{\text{c}}/t_1}{W/t_2}[/latex]

where:

  • [latex]Q_{\text{c}}[/latex] is the heat removed (in British thermal units, Btu),
  • [latex]t_1[/latex] is the cooling time in hours,
  • [latex]W[/latex] is the electrical work input (in joules),
  • [latex]t_2[/latex] is the time for which work is done (in seconds).

Problem-Solving Strategies for Thermodynamics

  1. Identify whether heat, work, or internal energy are involved. Heat engines, refrigerators, and heat pumps all involve these energy flows.
  2. Define the system and draw a labeled energy diagram. This helps visualize where energy enters and exits.
  3. Determine what is unknown. Is it [latex]W[/latex], [latex]Q_{\text{c}}[/latex], [latex]Q_{\text{h}}[/latex], or a COP value?
  4. List what is known or can be inferred. Pay careful attention to which energy flows in and which flows out. Note if the process is isothermal or adiabatic.
  5. Solve the appropriate equations. Choose between [latex]{\text{COP}}_{\text{hp}}[/latex], [latex]{\text{COP}}_{\text{ref}}[/latex], or [latex]\text{Eff}[/latex] based on context.
  6. Insert values with units and compute the result. Double-check for correct unit conversions, especially when using Btu, hours, or seconds.
  7. Check for reasonableness. Remember, [latex]\text{Eff} 1[/latex], but [latex]{\text{COP}} > 1[/latex] in practical applications.

Section Summary

  • Heat pumps can transfer energy from cold outside air to warm indoor spaces, thanks to work input that drives the cycle.
  • The coefficient of performance for a heat pump is [latex]{\text{COP}}_{\text{hp}} = \frac{Q_{\text{h}}}{W}[/latex], and it is typically greater than 1.
  • Refrigerators and air conditioners are also heat pumps, but their goal is cooling. Their performance is measured by [latex]{\text{COP}}_{\text{ref}} = \frac{Q_{\text{c}}}{W}[/latex].
  • Energy Efficiency Ratios (EERs) offer practical ways to compare appliance performance, even if they are not in SI units.

Conceptual Questions

  1. Explain why heat pumps do not work as well in very cold climates as they do in milder ones. Is the same true of refrigerators?
  2. In some Northern European nations, homes are being built without heating systems of any type. They are very well insulated and are kept warm by the body heat of the residents. However, when the residents are not at home, it is still warm in these houses. What is a possible explanation?
  3. Why do refrigerators, air conditioners, and heat pumps operate most cost-effectively for cycles with a small difference between [latex]{T}_{\text{h}}[/latex] and [latex]{T}_{\text{c}}[/latex]? (Note that the temperatures of the cycle employed are crucial to its [latex]\text{COP}[/latex].)
  4. Grocery store managers contend that there is less total energy consumption in the summer if the store is kept at a low temperature. Make arguments to support or refute this claim, taking into account that there are numerous refrigerators and freezers in the store.
  5. Can you cool a kitchen by leaving the refrigerator door open?

Problem Exercises

  1. What is the coefficient of performance of an ideal heat pump that has heat transfer from a cold temperature of [latex]-\text{25}\text{.}0\text{º}\text{C}[/latex] to a hot temperature of [latex]\text{40}\text{.}0\text{º}\text{C}[/latex]?
  2. Suppose you have an ideal refrigerator that cools an environment at [latex]-\text{20}\text{.}0\text{º}\text{C}[/latex] and has heat transfer to another environment at [latex]\text{50}\text{.}0\text{º}\text{C}[/latex]. What is its coefficient of performance?
  3. What is the best coefficient of performance possible for a hypothetical refrigerator that could make liquid nitrogen at [latex]-\text{200}\text{º}\text{C}[/latex] and has heat transfer to the environment at [latex]\text{35}\text{.}0\text{º}\text{C}[/latex]?
  4. In a very mild winter climate, a heat pump has heat transfer from an environment at [latex]5\text{.}\text{00}\text{º}\text{C}[/latex] to one at [latex]\text{35}\text{.}0\text{º}\text{C}[/latex]. What is the best possible coefficient of performance for these temperatures?
  5. (a) What is the best coefficient of performance for a heat pump that has a hot reservoir temperature of [latex]\text{50}\text{.}0\text{º}\text{C}[/latex] and a cold reservoir temperature of [latex]-\text{20}\text{.0ºC}[/latex]? (b) How much heat transfer occurs into the warm environment if [latex]3\text{.60}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] of work ([latex]\text{10}\text{.}0\text{kW}\cdot \text{h}[/latex]) is put into it? (c) If the cost of this work input is [latex]\text{10.0 cents/kW}\cdot \text{h}[/latex], how does its cost compare with the direct heat transfer achieved by burning natural gas at a cost of 85.0 cents per therm. (A therm is a common unit of energy for natural gas and equals [latex]1\text{.}\text{055}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex].)
  6. (a) What is the best coefficient of performance for a refrigerator that cools an environment at [latex]-\text{30}\text{.}0\text{º}\text{C}[/latex] and has heat transfer to another environment at [latex]\text{45}\text{.}0º\text{C}[/latex]? (b) How much work in joules must be done for a heat transfer of 4186 kJ from the cold environment? (c) What is the cost of doing this if the work costs 10.0 cents per [latex]3\text{.}\text{60}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] (a kilowatt-hour)? (d) How many kJ of heat transfer occurs into the warm environment? (e) Discuss what type of refrigerator might operate between these temperatures.
  7. Suppose you want to operate an ideal refrigerator with a cold temperature of [latex]-\text{10}\text{.}0º\text{C}[/latex], and you would like it to have a coefficient of performance of 7.00. What is the hot reservoir temperature for such a refrigerator?
  8. An ideal heat pump is being considered for use in heating an environment with a temperature of [latex]\text{22}\text{.}0\text{º}\text{C}[/latex]. What is the cold reservoir temperature if the pump is to have a coefficient of performance of 12.0?
  9. A 4-ton air conditioner removes [latex]5\text{.}\text{06}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] (48,000 British thermal units) from a cold environment in 1.00 h. (a) What energy input in joules is necessary to do this if the air conditioner has an energy efficiency rating ([latex]\text{EER}[/latex]) of 12.0? (b) What is the cost of doing this if the work costs 10.0 cents per [latex]3\text{.}\text{60}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] (one kilowatt-hour)? (c) Discuss whether this cost seems realistic. Note that the energy efficiency rating ([latex]\text{EER}[/latex]) of an air conditioner or refrigerator is defined to be the number of British thermal units of heat transfer from a cold environment per hour divided by the watts of power input.
  10. Show that the coefficients of performance of refrigerators and heat pumps are related by [latex]{\text{COP}}_{\text{ref}}={\text{COP}}_{\text{hp}}-1[/latex].
  11. Start with the definitions of the [latex]\text{COP}[/latex] s and the conservation of energy relationship between [latex]{Q}_{\text{h}}[/latex], [latex]{Q}_{\text{c}}[/latex], and [latex]W[/latex].

Glossary

heat pump
a machine that generates heat transfer from cold to hot
coefficient of performance
for a heat pump, it is the ratio of heat transfer at the output (the hot reservoir) to the work supplied; for a refrigerator or air conditioner, it is the ratio of heat transfer from the cold reservoir to the work supplied
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book