"

Statics and Torque

63 Applications of Statics, Including Problem-Solving Strategies

Learning Objectives

  • Discuss the applications of Statics in real life.
  • State and discuss various problem-solving strategies in Statics.

Statics has wide-ranging applications, from understanding the balance of architectural structures like bridges and buildings to analyzing muscle forces and joint torques in the human body. In this section, we begin with strategies specifically tailored to solve problems in statics. Since statics is a special case of Newton’s laws, the general problem-solving methods you’ve already encountered still apply.

Problem-Solving Strategy: Static Equilibrium Situations

  1. Determine whether the system is in static equilibrium. This is the case if the acceleration of the system is zero and there is no angular acceleration.
  2. Draw a free-body diagram for the object or system of interest. Carefully label all forces, noting their magnitudes, directions, and points of application where known.
  3. Apply the two conditions for equilibrium:
    [latex]\text{net}\ F = 0[/latex]
    [latex]\text{net}\ \tau = 0[/latex]

    Choose a pivot point that simplifies torque calculations. The best choices make torques from unknown forces equal to zero (for example, when the line of action passes through the pivot, [latex]\theta = 0[/latex], or the force acts at the pivot so that [latex]r = 0[/latex]). Always choose a convenient coordinate system.

  4. Check your solution for reasonableness. Consider the magnitude, direction, and units of the final answer. Judging reasonableness becomes easier with experience.

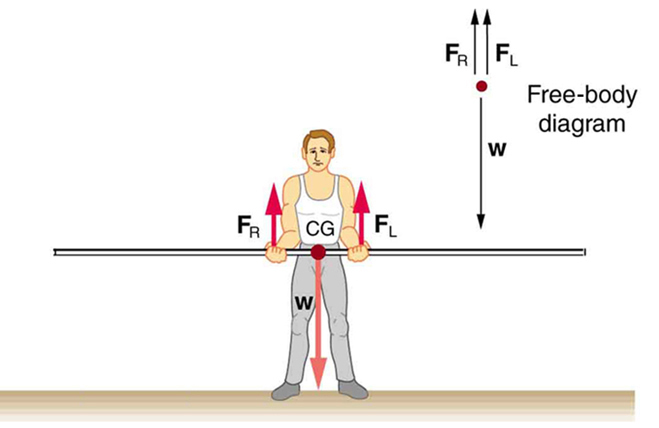
Let’s apply this strategy to the situation shown in Figure 63.1. A pole vaulter holds a uniform pole of mass 5.00 kg. The center of gravity (cg) of the pole is midway between the vaulter’s hands. Each hand exerts a force equal to half the pole’s weight, that is:

[latex]F_R = F_L = \frac{w}{2} = \frac{mg}{2} = \frac{(5.00\ \text{kg})(9.80\ \text{m/s}^2)}{2} = 24.5\ \text{N}[/latex]

This satisfies the condition for translational equilibrium, [latex]\text{net}\ F = 0[/latex]. It also satisfies rotational equilibrium, [latex]\text{net}\ \tau = 0[/latex], if we take the pivot point to be at the center of gravity. In this case, the torques from each hand are equal and opposite, and the weight exerts no torque about the pivot since its lever arm is zero.

This example demonstrates a principle: if forces are applied symmetrically about the center of gravity, each support shares the load equally. A uniform table with four legs supports its weight equally—each leg bears one-fourth the weight.

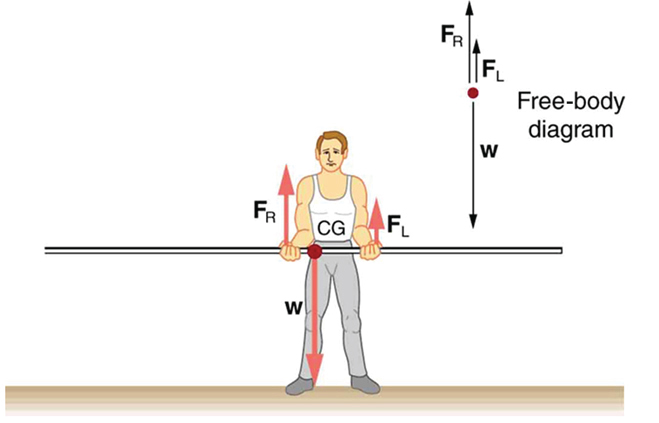
Now consider Figure 63.2, where the vaulter shifts the pole so that the cg is closer to the right hand. The total force must still equal the weight of the pole, but now the torques differ because the lever arms are unequal. The right hand supports more of the weight. If the right hand is placed directly under the cg, it would support the full weight by itself. This situation is analogous to two people carrying a load—whoever is closer to the cg carries more of the load.

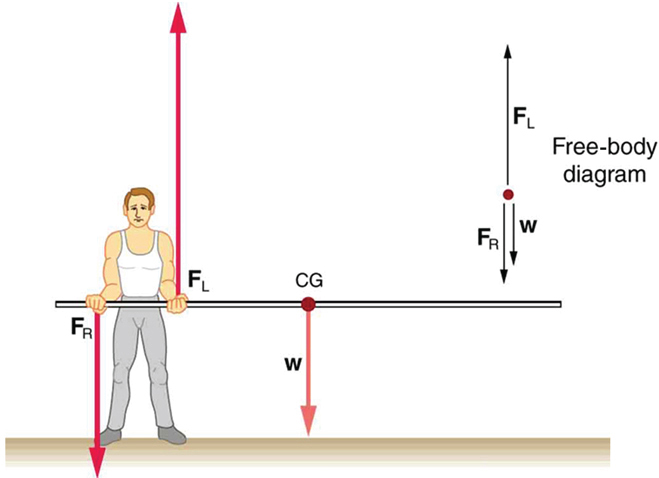
In Figure 63.3, the vaulter shifts the pole even further so that the cg lies beyond his left hand. This results in a dramatic shift: the right hand must now apply a downward force while the left hand applies an upward one. The forces are no longer both supporting the weight; one pushes down, and the other pushes up, forming a torque pair.

A pole vaulter is standing on the ground holding a pole with his two hands. The center of gravity of the pole is between the hands of the pole vaulter and is near the right hand of the man. The weight W is shown as an arrow downward toward center of gravity. The reactions F sub R and F sub L of the hands of the man are shown with vectors in upward direction. A free body diagram of the situation is shown on the top right side of the figure.
Figure 63.1: A pole vaulter holds a uniform pole such that its center of gravity lies midway between his hands. The forces from both hands are equal and point upward, balancing the weight.
A pole vaulter is standing on the ground holding a pole with his two hands. The center of gravity of the pole is between the hands of the pole vaulter and is near the right hand of the man. The weight W is shown as an arrow downward toward center of gravity. The reactions F sub R and F sub L of the hands of the man are shown with vectors in upward direction. A free body diagram of the situation is shown on the top right side of the figure.
Figure 63.2: The pole’s center of gravity lies closer to the vaulter’s right hand, so the right hand must exert a greater upward force than the left.
A pole vaulter is standing on the ground holding a pole from one side with his two hands. The centre of gravity of the pole is to the left of the pole vaulter. The weight W is shown as an arrow downward at center of gravity. The reaction F sub R is shown with a vector pointing downward from the man’s right hand and F sub L is shown with a vector in upward direction at the location of the man’s left hand. A free body diagram of the situation is shown on the top right side of the figure.
Figure 63.3: The center of gravity lies to the left of the vaulter’s body. The left hand pushes upward and the right hand downward to maintain balance—demonstrating torque equilibrium.
Try this yourself with a meter stick or broom handle. Hold it horizontally and vary the point where your hands support it. You’ll feel the difference in required forces—an intuitive demonstration of torque balance in everyday life.

Example 63.1: What Force Is Needed to Support a Weight Held Near Its CG?

For the situation shown in Figure 63.2, calculate: (a) [latex]{F}_{R}[/latex] , the force exerted by the right hand, and (b) [latex]{F}_{L}[/latex], the force exerted by the left hand. The hands are 0.900 m apart, and the cg of the pole is 0.600 m from the left hand.

Strategy

Figure 63.2 includes a free body diagram for the pole, the system of interest. There is not enough information to use the first condition for equilibrium [latex]\text{(net}\phantom{\rule{0.25em}{0ex}}F=0[/latex]), since two of the three forces are unknown and the hand forces cannot be assumed to be equal in this case. There is enough information to use the second condition for equilibrium [latex]\text{(net}\phantom{\rule{0.25em}{0ex}}\tau =0\text{)}[/latex] if the pivot point is chosen to be at either hand, thereby making the torque from that hand zero. We choose to locate the pivot at the left hand in this part of the problem, to eliminate the torque from the left hand.

Solution for (a)

There are now only two nonzero torques, those from the gravitational force ([latex]{\tau }_{\text{w}}[/latex]) and from the push or pull of the right hand ([latex]{\tau }_{R}[/latex]). Stating the second condition in terms of clockwise and counterclockwise torques,

[latex]\text{net}\phantom{\rule{0.25em}{0ex}}{\tau }_{\text{cw}}=\text{–net}\phantom{\rule{0.25em}{0ex}}{\tau }_{\text{ccw}}\text{.}[/latex]

or the algebraic sum of the torques is zero.

Here this is

[latex]{\tau }_{R}={\mathrm{–\tau }}_{\text{w}}[/latex]

since the weight of the pole creates a counterclockwise torque and the right hand counters with a clockwise torque. Using the definition of torque, [latex]\tau =\text{rF}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta[/latex], noting that [latex]\theta =90º[/latex] , and substituting known values, we obtain

[latex]\left(0\text{.}\text{900 m}\right)\left({F}_{R}\right)=\left(0\text{.600 m}\right)\left(\mathit{mg}\right)\text{.}[/latex]

Thus,

[latex]\begin{array}{lll}{F}_{R}& =& \left(0.667\right)\left(\text{5.00 kg}\right)\left(9.80\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)\\ & =& \text{32.7 N.}\end{array}[/latex]

Solution for (b)

The first condition for equilibrium is based on the free body diagram in the figure. This implies that by Newton’s second law:

[latex]{F}_{L}+{F}_{R}–\text{mg}=0[/latex]

From this we can conclude:

[latex]{F}_{L}+{F}_{R}=w=\text{mg}[/latex]

Solving for [latex]{F}_{L}[/latex], we obtain

[latex]\begin{array}{lll}{F}_{L}& =& \mathit{mg}-{F}_{R}\\ & =& \mathit{mg}-\text{32}\text{.}7 N\\ & =& \left(\text{5.00 kg}\right)\left(\text{9.80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)-\text{32.7 N}\\ & =& \text{16.3 N}\end{array}[/latex]

Discussion

[latex]{F}_{L}[/latex] is seen to be exactly half of [latex]{F}_{R}[/latex], as we might have guessed, since [latex]{F}_{L}[/latex] is applied twice as far from the cg as [latex]{F}_{R}[/latex].

If the pole vaulter holds the pole as he might at the start of a run, shown in Figure 63.3 the forces change again. Both are considerably greater, and one force reverses direction.

Take-Home Experiment — Balancing on a Moving Bus

This is an experiment to try while riding a bus or train. First, stand facing sideways (perpendicular to the direction of motion). As the vehicle accelerates or decelerates, how do you shift your body to stay balanced? Next, stand facing forward (in the direction of motion). How do you readjust your mass distribution in this position?

Which stance—sideways or forward—makes it easier and safer to remain stable during motion? Why?

Hint: Consider how your base of support and the direction of inertia affect your stability.

Important: For your safety and that of others, always hold onto a railing or support while performing this activity!

PhET Explorations: Balancing Act

Play with objects on a teeter-totter to learn about torque and rotational balance. Try different masses at different distances and observe how equilibrium is achieved. Test your understanding by attempting the interactive Balance Challenge game.

Summary

  • Statics can be applied to a variety of situations, ranging from raising a drawbridge to bad posture and back strain. We have discussed the problem-solving strategies specifically useful for statics. Statics is a special case of Newton’s laws, both the general problem-solving strategies and the special strategies for Newton’s laws, discussed in Problem-Solving Strategies, still apply.

Conceptual Questions

  1. When visiting some countries, you may see a person balancing a load on the head. Explain why the center of mass of the load needs to be directly above the person’s neck vertebrae.

Problems & Exercises

  1. To get up on the roof, a person (mass 70.0 kg) places a 6.00-m aluminum ladder (mass 10.0 kg) against the house on a concrete pad with the base of the ladder 2.00 m from the house. The ladder rests against a plastic rain gutter, which we can assume to be frictionless. The center of mass of the ladder is 2 m from the bottom. The person is standing 3 m from the bottom. What are the magnitudes of the forces on the ladder at the top and bottom?
  2. In Figure 63.3, the cg of the pole held by the pole vaulter is 2.00 m from the left hand, and the hands are 0.700 m apart. Calculate the force exerted by (a) his right hand and (b) his left hand. (c) If each hand supports half the weight of the pole in Figure 63.1, show that the second condition for equilibrium [latex]\text{(net}\phantom{\rule{0.25em}{0ex}}{\tau }_{}=\text{0)}[/latex] is satisfied for a pivot other than the one located at the center of gravity of the pole. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium described above.

Glossary

static equilibrium
equilibrium in which the acceleration of the system is zero and accelerated rotation does not occur
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book