Rotational Motion and Angular Momentum

67 Angular Acceleration

Learning Objectives

  • Describe uniform circular motion.
  • Explain non-uniform circular motion.
  • Calculate angular acceleration of an object.
  • Observe the link between linear and angular acceleration.

In the chapter on Uniform Circular Motion and Gravitation, we examined the case of motion along a circular path at constant speed. This is known as uniform circular motion. In this case, the angular velocity [latex]\omega[/latex] remains constant. Angular velocity is defined as the time rate of change of the rotation angle [latex]\theta[/latex]:

[latex]\omega = \frac{\Delta \theta}{\Delta t}[/latex]

Here, [latex]\theta[/latex] is measured in radians and represents the angle of rotation, as illustrated in Figure 67.1. The relationship between angular velocity [latex]\omega[/latex] and linear velocity [latex]v[/latex] is given by:

[latex]v = r\omega[/latex]

or equivalently,

[latex]\omega = \frac{v}{r}[/latex]

where [latex]r[/latex] is the radius of curvature. In the standard sign convention, angular quantities that proceed counterclockwise are positive, while clockwise rotations are negative.

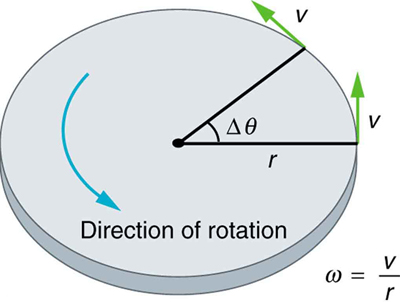
The given figure shows counterclockwise circular motion with a horizontal line, depicting radius r, drawn from the center of the circle to the right side on its circumference and another line is drawn in such a manner that it makes an acute angle delta theta with the horizontal line. Tangential velocity vectors are indicated at the end of the two lines. At the bottom right side of the figure, the formula for angular velocity is given as v upon r.
Figure 67.1: Uniform circular motion involves constant speed around a circle. The relationship between angular velocity [latex]\omega[/latex] and linear velocity [latex]v[/latex] is shown geometrically.

However, in many real-world situations, angular velocity is not constant. For instance, a figure skater pulling in their arms spins faster, a merry-go-round speeds up as a child pushes it, and a hard disk decelerates when powered off. In each of these cases, angular velocity changes over time—this is angular acceleration. Angular acceleration, symbolized as [latex]\alpha[/latex], is defined as the rate of change of angular velocity over time:

[latex]\alpha = \frac{\Delta \omega}{\Delta t}[/latex]

Here, [latex]\Delta \omega[/latex] is the change in angular velocity and [latex]\Delta t[/latex] is the time interval over which the change occurs. The SI unit of angular acceleration is radians per second squared ([latex]\text{rad/s}^2[/latex]). A positive value of [latex]\alpha[/latex] indicates increasing angular velocity (speeding up), while a negative value indicates decreasing angular velocity (slowing down).

Example 67.1: Calculating the Angular Acceleration and Deceleration of a Bike Wheel

Suppose a teenager puts her bicycle on its back and starts the rear wheel spinning from rest to a final angular velocity of 250 rpm in 5.00 s.

  1. Calculate the angular acceleration in [latex]{\text{rad/s}}^{2}[/latex].
  2. If she now slams on the brakes, causing an angular acceleration of [latex]–87.3\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}[/latex], how long does it take the wheel to stop?

Strategy for (a)

The angular acceleration can be found directly from its definition in [latex]\alpha =\frac{\Delta \omega }{\Delta t}[/latex] because the final angular velocity and time are given. We see that [latex]\Delta \omega[/latex] is 250 rpm and [latex]\Delta t[/latex] is 5.00 s.

Solution for (a)

Entering known information into the definition of angular acceleration, we get

[latex]\begin{array}{lll}\alpha & =& \frac{\Delta \omega }{\Delta t}\\ & =& \frac{\text{250 rpm}}{\text{5.00 s}}\end{array}[/latex]

Because [latex]\Delta \omega[/latex] is in revolutions per minute (rpm) and we want the standard units of [latex]{\text{rad/s}}^{2}[/latex] for angular acceleration, we need to convert [latex]\Delta \omega[/latex] from rpm to rad/s:

[latex]\begin{array}{lll}\Delta \omega & =& \text{250}\frac{\text{rev}}{\text{min}}\cdot \frac{\text{2π rad}}{\text{rev}}\cdot \frac{\text{1 min}}{\text{60 sec}}\\ & =& \text{26.2}\frac{\text{rad}}{\text{s}}\end{array}[/latex]

Entering this quantity into the expression for [latex]\alpha[/latex], we get

[latex]\begin{array}{lll}\alpha & =& \frac{\Delta \omega }{\Delta t}\\ & =& \frac{\text{26.2 rad/s}}{\text{5.00 s}}\\ & =& \text{5.24}{\text{ rad/s}}^{2}\end{array}[/latex]

Strategy for (b)

In this part, we know the angular acceleration and the initial angular velocity. We can find the stoppage time by using the definition of angular acceleration and solving for [latex]\Delta t[/latex], yielding

[latex]\Delta t=\frac{\Delta \omega }{\alpha }[/latex]

Solution for (b)

Here, the angular velocity decreases from [latex]\text{26.2 rad/s}[/latex] (250 rpm) to zero, so [latex]\Delta \omega[/latex] is [latex]–\text{26.2 rad/s}[/latex] and [latex]\alpha[/latex] is given to be [latex]–\text{87.3}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}[/latex]. Thus,

[latex]\begin{array}{lll}\Delta t& =& \frac{–\text{26.2 rad/s}}{–\text{87.3}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}}\\ & =& \text{0.300 s}\end{array}[/latex]

Discussion

Note that the angular acceleration as the girl spins the wheel is small and positive; it takes 5 s to produce an appreciable angular velocity. When she hits the brake, the angular acceleration is large and negative. The angular velocity quickly goes to zero. In both cases, the relationships are analogous to what happens with linear motion. For example, there is a large deceleration when you crash into a brick wall—the velocity change is large in a short time interval.

Imagine if the bicycle from the previous example had been resting on its wheels rather than upside-down. It would have accelerated forward, rolling along the ground before coming to a stop. This example reveals an important connection between circular motion and linear motion. Specifically, how are linear acceleration and angular acceleration related? In circular motion, linear acceleration is directed tangent to the circle at the point of interest. As shown in Figure 67.2, this kind of acceleration is called tangential acceleration and is denoted [latex]a_{\text{t}}[/latex].

In the figure, a semicircle is drawn, with its radius r, shown here as a line segment. The anti-clockwise motion of the circle is shown with an arrow on the path of the circle. Tangential velocity vector, v, of the point, which is on the meeting point of radius with the circle, is shown as a green arrow and the linear acceleration, a-t is shown as a yellow arrow in the same direction along v.
Figure 67.2: In circular motion, the linear acceleration [latex]a_{\text{t}}[/latex] occurs as a change in the magnitude of velocity. It acts tangentially to the circle at the point of motion.

Tangential Acceleration

[latex]a_{\text{t}}[/latex] refers to the rate of change of speed (magnitude of velocity) along the circular path, but it does not affect the direction of motion. Meanwhile, centripetal acceleration, denoted [latex]a_{\text{c}}[/latex], changes the direction of the velocity vector, not its magnitude. This acceleration always points inward toward the center of the circle, keeping the object moving along a curved path, as seen in Figure 67.3.

In the figure, a semicircle is drawn, with its radius r, shown here as a line segment. The anti-clockwise motion of the circle is shown with an arrow on the path of the circle. Tangential velocity vector, v, of the point, which is on the meeting point of radius with the circle, is shown as a green arrow and the linear acceleration, a sub t is shown as a yellow arrow in the same direction along v. The centripetal acceleration, a sub c, is also shown as a yellow arrow drawn perpendicular to a sub t, toward the direction of the center of the circle. A label in the figures states a sub t affects magnitude and a sub c affects direction.
Figure 67.3: Tangential acceleration [latex]a_{\text{t}}[/latex] changes the magnitude of velocity, while centripetal acceleration [latex]a_{\text{c}}[/latex] changes the direction. These two vectors are always perpendicular to one another.

We can now express the relationship between tangential (linear) acceleration [latex]a_{\text{t}}[/latex] and angular acceleration [latex]\alpha[/latex]. Recall from linear kinematics that:

[latex]a_{\text{t}} = \frac{\Delta v}{\Delta t}[/latex]

In circular motion, since [latex]v = r\omega[/latex], we substitute:

[latex]a_{\text{t}} = \frac{\Delta (r\omega)}{\Delta t}[/latex]

Because [latex]r[/latex] is constant for a given path, we factor it out:

[latex]a_{\text{t}} = r\frac{\Delta \omega}{\Delta t}[/latex]

But the rate of change of angular velocity is angular acceleration [latex]\alpha[/latex], so we have:

[latex]a_{\text{t}} = r\alpha[/latex]

This formula directly links angular and linear acceleration. We can also rearrange it to express angular acceleration in terms of linear acceleration:

[latex]\alpha = \frac{a_{\text{t}}}{r}[/latex]

These equations show that tangential acceleration is proportional to angular acceleration. The larger the angular acceleration, the larger the tangential acceleration. The radius [latex]r[/latex] also matters: for a given [latex]\alpha[/latex], a larger radius leads to greater linear acceleration, and vice versa. Example: Consider the wheels of a car. If the angular acceleration of the wheels increases, so does the car’s linear acceleration. However, a car with smaller wheels would experience smaller tangential acceleration for the same angular acceleration.

Example 67.2: Calculating the Angular Acceleration of a Motorcycle Wheel

A powerful motorcycle can accelerate from 0 to 30.0 m/s (about 108 km/h) in 4.20 s. What is the angular acceleration of its 0.320-m-radius wheels? (See Figure 67.4.)

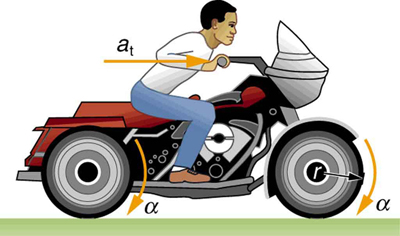
The figure shows the right side view of a man riding a motorcycle hence, depicting linear acceleration a of the motorcycle pointing toward the front of the bike as a horizontal arrow and the angular acceleration alpha of its wheels, shown here as curved arrows along the front of both the wheels pointing downward.
Figure 67.4: The linear acceleration of a motorcycle is accompanied by an angular acceleration of its wheels.

Strategy

We are given information about the linear velocities of the motorcycle. Thus, we can find its linear acceleration [latex]{a}_{\text{t}}[/latex]. Then, the expression [latex]\alpha =\frac{{a}_{\text{t}}}{r}[/latex] can be used to find the angular acceleration.

Solution

The linear acceleration is

[latex]\begin{array}{lll}{a}_{\text{t}}& =& \frac{\Delta v}{\Delta t}\\ & =& \frac{\text{30.0 m/s}}{\text{4.20 s}}\\ & =& \text{7.14}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\end{array}[/latex]

We also know the radius of the wheels. Entering the values for [latex]{a}_{\text{t}}[/latex] and [latex]r[/latex] into

[latex]\alpha =\frac{{a}_{\text{t}}}{r}[/latex], we get

[latex]\begin{array}{lll}\alpha & =& \frac{{a}_{\text{t}}}{r}\\ & =& \frac{\text{7.14}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}}{\text{0.320 m}}\\ & =& \text{22.3}\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}\end{array}[/latex]

Discussion

Units of radians are dimensionless and appear in any relationship between angular and linear quantities.

So far, we have introduced three key rotational kinematic quantities:

  • Angular displacement [latex]\theta[/latex]
  • Angular velocity [latex]\omega[/latex]
  • Angular acceleration [latex]\alpha[/latex]

These quantities are rotational analogs of the familiar translational motion quantities:

  • Displacement [latex]x[/latex]
  • Velocity [latex]v[/latex]
  • Acceleration [latex]a[/latex]

Table 67.1 summarizes the correspondence between rotational and translational quantities, along with their defining relationships. This analogy provides the foundation for analyzing rotational motion using tools and concepts similar to those used in linear motion.

Table 67.1: Rotational and Translational Quantities
Rotational Translational Relationship
[latex]\theta[/latex] [latex]x[/latex] [latex]\theta =\frac{x}{r}[/latex]
[latex]\omega[/latex] [latex]v[/latex] [latex]\omega =\frac{v}{r}[/latex]
[latex]\alpha[/latex] [latex]a[/latex] [latex]\alpha =\frac{{a}_{t}}{r}[/latex]

In the next section, we will use these analogs to derive rotational versions of the kinematic equations, allowing us to solve problems involving angular displacement, angular velocity, and angular acceleration in a manner similar to linear motion.

Take-Home Experiment

Sit on a swivel chair with your feet flat on the ground. Straighten one of your legs so it extends horizontally outward. Using your other leg, gently push against the ground to initiate rotation. After a few pushes, stop applying force and allow the chair to rotate freely. Your task is to track and analyze the motion of your extended leg, treating it as a point rotating about a central vertical axis (the pivot under the chair). From the moment rotation begins:

  • Sketch the angular displacement [latex]\theta(t)[/latex] as a function of time.
  • Sketch the angular velocity [latex]\omega(t)[/latex] as a function of time.
  • Sketch the angular acceleration [latex]\alpha(t)[/latex] as a function of time.

You should observe a brief period of increasing angular velocity (and therefore positive angular acceleration) while you’re actively pushing, followed by a near-constant or slowly decreasing angular velocity once the chair spins freely (due to air resistance and friction in the chair mechanism). Based on your observations, estimate approximate magnitudes for each of these quantities over time. This activity helps illustrate how angular displacement, angular velocity, and angular acceleration vary in real-world rotational motion. You may also find this experiment helpful in visualizing angular kinematics prior to graphing or calculating theoretical values in homework or exams.

Check Your Understanding

Angular acceleration is a vector, having both magnitude and direction. How do we denote its magnitude and direction? Illustrate with an example.

Answer: The magnitude of angular acceleration is [latex]\alpha[/latex], and its most common units are [latex]{\text{rad/s}}^{2}[/latex]. The direction of angular acceleration along a fixed axis is denoted by a plus or minus sign, just as the direction of linear acceleration in one dimension is denoted by a plus or minus sign. For example, consider a gymnast doing a forward flip. Her angular velocity vector would be parallel to the mat and point to her left (by the right-hand rule). If she is increasing her spin rate during the flip, her angular acceleration vector would point in the same direction as her angular velocity. The magnitude of her angular acceleration depends on how quickly she changes her angular velocity and on her moment of inertia about the spin axis.

Interactive Exploration: Ladybug Revolution

Rotational motion is all around us, from bicycle wheels and ceiling fans to the rotation of planets. In this simulation, you'll explore how an object's angular position, angular velocity, and angular acceleration determine its motion as it travels in a circular path. You'll also examine how these rotational quantities are related to the object's position, velocity, and acceleration in two dimensions. Experiment by rotating the merry-go-round manually or by setting a constant angular velocity or angular acceleration. Observe the ladybug's motion using both vectors and graphs, and compare how changes in the rotational motion affect the bug's position and movement around the circle.

Guided Exploration

As you interact with the simulation, try to answer the following questions:

  1. Rotate the merry-go-round slowly by hand. How does the ladybug's angular position change as it completes one full revolution?
  2. Set a constant angular velocity. What happens to the ladybug's speed and the direction of its velocity vector as it moves around the circle?
  3. Observe the acceleration vector during uniform circular motion. Does it point in the direction of motion or toward the center of the circle?
  4. Apply an angular acceleration. How does the angular velocity change over time? How does this affect the motion of the ladybug?
  5. Switch between the vector and graph displays. How are the graphs of angular position, angular velocity, and angular acceleration related to the ladybug's motion?
  6. Based on your observations, explain why an object moving in a circle can have constant speed while still experiencing acceleration.

After completing the exploration, compare your observations with the concepts presented in this section. Notice that rotational motion can be described using angular quantities that are directly analogous to the position, velocity, and acceleration used in linear motion. Even when an object moves at constant speed around a circle, its continuously changing direction means that it is accelerating toward the center of the circular path.

Healthcare Connection

The shoulder joint undergoes extremely high angular acceleration during a baseball pitch or tennis serve, spinning the arm through a large angle in a fraction of a second. Sports medicine research uses motion-capture systems to measure exactly this kind of angular acceleration at the shoulder and elbow, because the resulting torques on the rotator cuff tendons and ligaments are a major source of overuse injuries in throwing athletes. Understanding how quickly angular velocity changes during the throwing motion helps clinicians and coaches identify pitch counts, mechanics, and training loads that keep these accelerations—and the joint stress they cause—within a safer range.

Section Summary

  • Uniform circular motion is the motion with a constant angular velocity
    [latex]\omega =\frac{\Delta \theta }{\Delta t}[/latex]
  • In non-uniform circular motion, the velocity changes with time and the rate of change of angular velocity (i.e., angular acceleration) is
    [latex]\alpha =\frac{\Delta \omega }{\Delta t}[/latex]
  • Linear or tangential acceleration refers to changes in the magnitude of velocity but not its direction, given as
    [latex]{a}_{\text{t}}=\frac{\Delta v}{\Delta t}[/latex]
  • For circular motion, note that
    [latex]v = r\omega[/latex]

    so that

    [latex]{a}_{\text{t}}=\frac{\Delta (r\omega)}{\Delta t}[/latex]
  • The radius [latex]r[/latex] is constant for circular motion, and so
    [latex]\Delta (r\omega) = r\Delta \omega[/latex]

    Thus,

    [latex]{a}_{\text{t}}=r\frac{\Delta \omega}{\Delta t}[/latex]
  • By definition,
    [latex]\alpha = \frac{\Delta \omega}{\Delta t}[/latex]

    Thus,

    [latex]{a}_{\text{t}} = r\alpha[/latex]

    or

    [latex]\alpha = \frac{{a}_{\text{t}}}{r}[/latex]

Conceptual Questions

  1. Analogies exist between rotational and translational physical quantities. Identify the rotational term analogous to each of the following: acceleration, force, mass, work, translational kinetic energy, linear momentum, impulse.
  2. Explain why centripetal acceleration changes the direction of velocity in circular motion but not its magnitude.
  3. In circular motion, a tangential acceleration can change the magnitude of the velocity but not its direction. Explain your answer.
  4. Suppose a piece of food is on the edge of a rotating microwave oven plate. Does it experience nonzero tangential acceleration, centripetal acceleration, or both when:
    1. The plate starts to spin?
    2. The plate rotates at constant angular velocity?
    3. The plate slows to a halt?

Problems & Exercises

  1. At its peak, a tornado is 60.0 m in diameter and carries 500 km/h winds. What is its angular velocity in revolutions per second?
  2. Integrated Concepts: An ultracentrifuge accelerates from rest to 100,000 rpm in 2.00 min.
    1. What is its angular acceleration in [latex]{\text{rad/s}}^{2}[/latex]?
    2. What is the tangential acceleration of a point 9.50 cm from the axis of rotation?
    3. What is the radial acceleration in [latex]{\text{m/s}}^{2}[/latex] and multiples of [latex]g[/latex] of this point at full rpm?
  3. Integrated Concepts: You have a grindstone (a disk) that is 90.0 kg, has a 0.340-m radius, and is turning at 90.0 rpm, and you press a steel axe against it with a radial force of 20.0 N.
    1. Assuming the kinetic coefficient of friction between steel and stone is 0.20, calculate the angular acceleration of the grindstone.
    2. How many turns will the stone make before coming to rest?
  4. Unreasonable Results: You are told that a basketball player spins the ball with an angular acceleration of [latex]\text{100}{\text{ rad/s}}^{2}[/latex].
    1. What is the ball’s final angular velocity if the ball starts from rest and the acceleration lasts 2.00 s?
    2. What is unreasonable about the result?
    3. Which premises are unreasonable or inconsistent?

Glossary

angular acceleration
the rate of change of angular velocity with time
change in angular velocity
the difference between final and initial values of angular velocity
tangential acceleration
the acceleration in a direction tangent to the circle at the point of interest in circular motion
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Introductory Physics for the Health and Life Sciences I Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book