Kinematics
11 Acceleration
Learning Objectives
- Define and distinguish between instantaneous acceleration, average acceleration, and deceleration.
- Calculate acceleration given initial time, initial velocity, final time, and final velocity.

In everyday language, the word “acceleration” usually means speeding up. And while this is certainly one case of acceleration, in physics, acceleration refers more broadly to any change in velocity—whether an object is speeding up, slowing down, or changing direction.
Average Acceleration
Average acceleration is defined as the change in velocity divided by the time interval over which that change occurs:
[latex]\bar{a} = \frac{\Delta v}{\Delta t} = \frac{v_{f} - v_{0}}{t_{f} - t_{0}}[/latex]
Here:
- [latex]\bar{a}[/latex] is the average acceleration,
- [latex]v_{f}[/latex] and [latex]v_{0}[/latex] are the final and initial velocities,
- [latex]t_{f}[/latex] and [latex]t_{0}[/latex] are the final and initial times.
The SI unit of acceleration is meters per second squared [latex](m/s^2)[/latex], which literally means how much the velocity changes every second.
For example, if a plane slows down as it comes in for a landing, its velocity decreases over time. The acceleration in this case is in the opposite direction to the motion—this is a key idea in understanding deceleration, or negative acceleration.
Acceleration as a Vector
Like velocity, acceleration is a vector quantity, meaning it has both magnitude and direction. That direction is determined by the direction of the change in velocity
. This means that an object can be accelerating even if its speed remains constant—if its direction is changing.
A classic example is a car turning a corner at a steady speed. Although the speed is unchanged, the direction of motion is changing, so the car is accelerating.

A common point of confusion arises when the acceleration of an object is in the opposite direction of its motion. This happens when an object slows down. In this case, the velocity and acceleration vectors point in opposite directions.
For instance, consider a subway train that decelerates as it approaches a station (see Figure 10.2). Even though the train is still moving forward, the acceleration is directed backward, against the motion.
This brings us to an important clarification:
Misconception Alert: Deceleration vs. Negative Acceleration
“Deceleration” refers to any situation in which the acceleration is in the opposite direction of the velocity—that is, the object is slowing down.
But “negative acceleration” refers only to the direction of acceleration in a coordinate system. Whether it causes an object to speed up or slow down depends on how the coordinate system is defined.
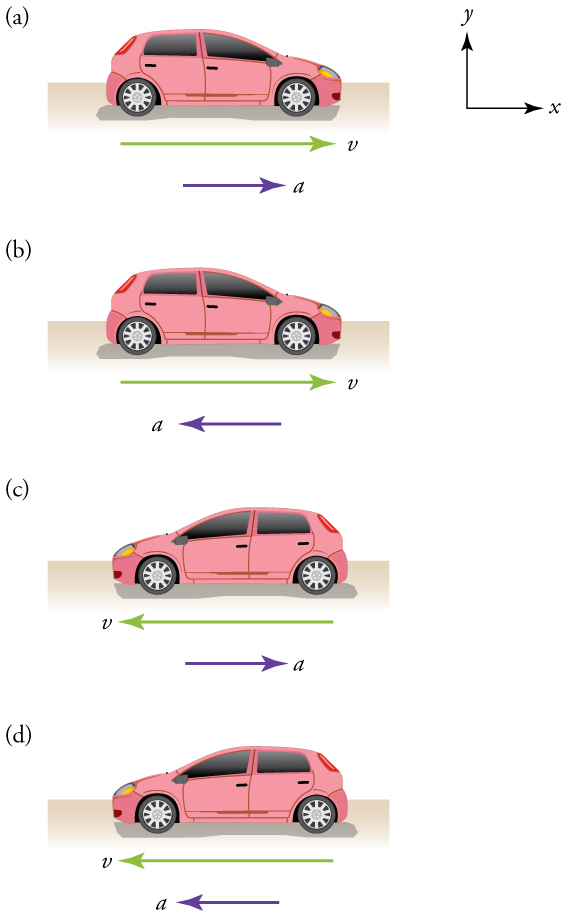
To make this clearer, look at the four cases illustrated in Figure 10.3:
-
(a) A car speeding up toward the right → positive acceleration
-
(b) A car slowing down toward the right → negative acceleration (also decelerating)
-
(c) A car slowing down toward the left → positive acceleration (but still decelerating)
-
(d) A car speeding up toward the left → negative acceleration, but not decelerating
As these cases show, the sign of acceleration depends on your chosen coordinate system. But deceleration always refers to a reduction in speed, regardless of direction.
Example 10.1: Calculating Acceleration: A Racehorse Leaves the Gate
A racehorse coming out of the gate accelerates from rest to a velocity of 15.0 m/s due west in 1.80 s. What is its average acceleration?

Strategy
First we draw a sketch and assign a coordinate system to the problem. This is a simple problem, but it always helps to visualize it. Notice that we assign east as positive and west as negative. Thus, in this case, we have negative velocity.
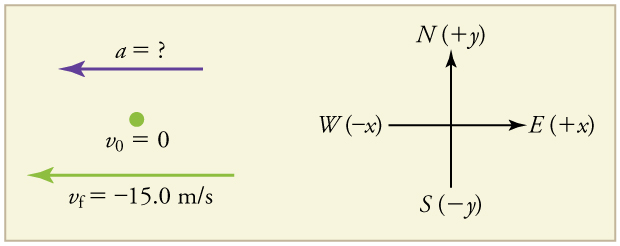
We can solve this problem by identifying [latex]\Delta v[/latex] and [latex]\Delta t[/latex] from the given information and then calculating the average acceleration directly from the equation [latex]\stackrel{-}{a}=\frac{\Delta v}{\Delta t}=\frac{{v}_{f}-{v}_{0}}{{t}_{f}-{t}_{0}}[/latex].
Solution
- Identify the knowns. [latex]{v}_{0}=0[/latex], [latex]{v}_{f}=-\text{15}\text{.0 m/s}[/latex] (the negative sign indicates direction toward the west), [latex]\Delta t=1\text{.80 s}[/latex].
- Find the change in velocity. Since the horse is going from zero to [latex]-\text{15.0 m/s}[/latex], its change in velocity equals its final velocity: [latex]\Delta v={v}_{f}=-\text{15}\text{.0 m/s}[/latex].
- Plug in the known values ([latex]\Delta v[/latex] and [latex]\Delta t[/latex]) and solve for the unknown [latex]\stackrel{-}{a}[/latex].
[latex]\stackrel{-}{a}=\frac{\Delta v}{\Delta t}=\phantom{\rule{0.15em}{0ex}}\frac{-\text{15}\text{.0 m/s}}{1\text{.80 s}}=-8\text{.33 m}{\text{/s}}^{2}.[/latex]
Discussion
The negative sign for acceleration indicates that acceleration is toward the west. An acceleration of [latex]8\text{.33 m}{\text{/s}}^{2}[/latex] due west means that the horse increases its velocity by 8.33 m/s due west each second, that is, 8.33 meters per second per second, which we write as [latex]8\text{.33 m}{\text{/s}}^{2}[/latex]. This is truly an average acceleration, because the ride is not smooth. We shall see later that an acceleration of this magnitude would require the rider to hang on with a force nearly equal to his weight.
Instantaneous Acceleration
Instantaneous acceleration [latex]a[/latex]—that is, the acceleration at a specific moment in time—is defined similarly to instantaneous velocity: it is the acceleration over an infinitesimally small time interval. In formal calculus-based physics, we define it as the derivative of velocity with respect to time. But in algebra-based physics, we can approximate it by using the average acceleration over very small time intervals when acceleration is approximately constant.
Choosing an Appropriate Approximation
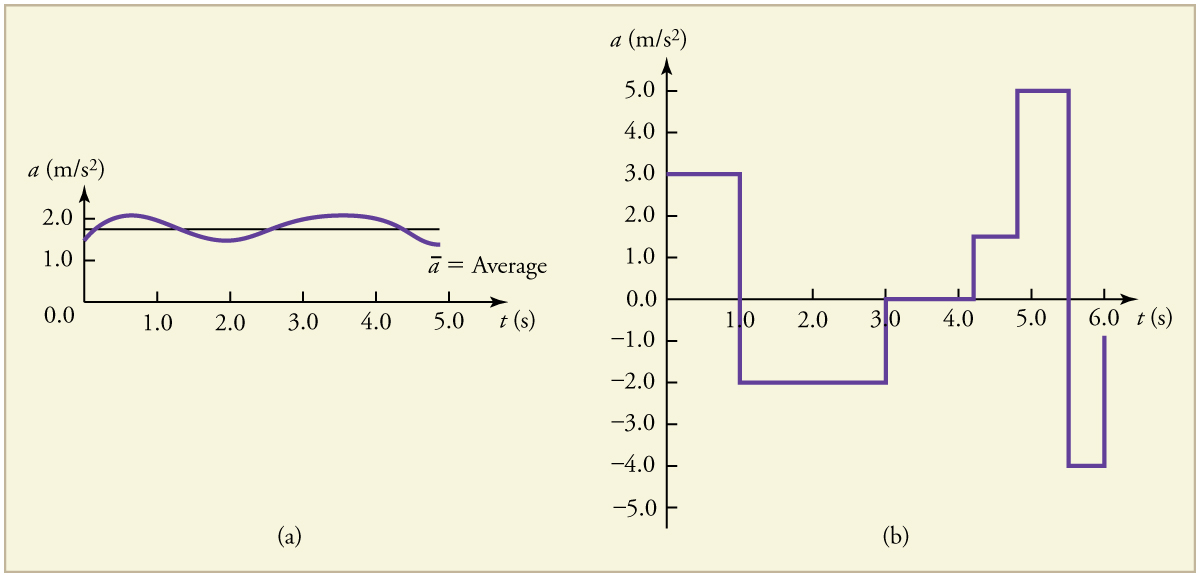
Figure 10.6 shows acceleration-versus-time graphs for two very different types of motion:
-
In Figure 10.6(a), acceleration varies only slightly and remains positive throughout the time interval. In such a case, we can treat the motion as having a constant acceleration equal to the average:
[latex]\bar{a} = \frac{\Delta v}{\Delta t}[/latex]
For this particular case, we might take [latex]\bar{a} \approx 1.8 , \text{m/s}^2[/latex].
-
In contrast, Figure 10.6(b) shows motion in which acceleration changes drastically. This could represent, for example, a package being pushed forward and backward irregularly on a conveyor belt. In this case, it’s best to break the motion into smaller intervals and calculate average acceleration for each:
For the interval from [latex]0[/latex] to [latex]1.0 , \text{s}[/latex]:
[latex]\bar{a}_{0-1} = +3.0 , \text{m/s}^2[/latex]
For the interval from [latex]1.0[/latex] to [latex]3.0 , \text{s}[/latex]:
[latex]\bar{a}_{1-3} = -2.0 , \text{m/s}^2[/latex]
This piecewise approach gives a better representation of the actual motion.
Subway Train Examples
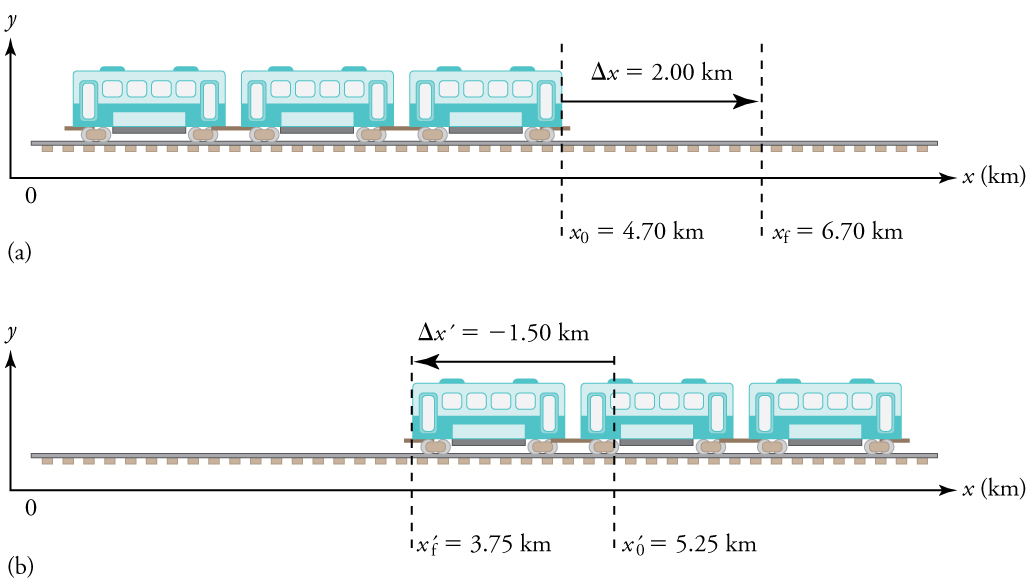
Figure 10.7 shows two one-dimensional motions of a subway train, where we have chosen the [latex]x[/latex]-axis such that motion to the right is positive and motion to the left is negative.
-
In Figure 10.7(a), the train moves to the right, from an initial position [latex]x_0[/latex] to a final position [latex]x_f[/latex], giving a positive displacement:
[latex]\Delta x = x_f - x_0 = +2.0 , \text{km}[/latex]
-
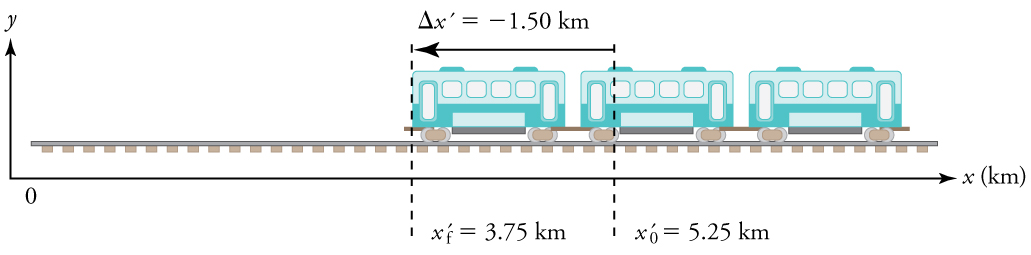
In Figure 10.7(b), the train moves to the left, from an initial position [latex]x'_0[/latex] to a final position [latex]x'_f[/latex], resulting in a negative displacement:
[latex]\Delta x' = x'_f - x'_0 = -1.5 , \text{km}[/latex]
In both cases, acceleration is a vector quantity, so it depends not only on how much velocity changes but also on the direction of that change. Acceleration in the same direction as motion increases speed, while acceleration in the opposite direction reduces it (i.e., deceleration).
The next several examples consider the motion of the subway train shown in . In (a) the shuttle moves to the right, and in (b) it moves to the left. The examples are designed to further illustrate aspects of motion and to illustrate some of the reasoning that goes into solving problems.
(a) Motion to the Right
In Figure 10.7(a), the subway train moves to the right, from an initial position [latex]x_0[/latex] to a final position [latex]x_f[/latex]. The displacement is:
[latex]\Delta x = x_f - x_0 = +2.0 , \text{km}[/latex]
Since the displacement is positive, we know the motion is in the positive [latex]x[/latex]-direction.
(b) Motion to the Left
In Figure 10.7(b), the train moves in the opposite direction, to the left, starting from a position [latex]x'_0[/latex] and ending at [latex]x'_f[/latex]. Here, the displacement is:
[latex]\Delta x' = x'_f - x'_0 = -1.5 , \text{km}[/latex]
The negative sign in [latex]\Delta x'[/latex] indicates that the motion is in the negative [latex]x[/latex]-direction.
Note: The prime symbol (′) is used to distinguish the second scenario from the first. Additionally, the scales of motion and the size of the train cars in the figure are adjusted for visual clarity and may not reflect a common scale.
Example 10.2: Calculating Displacement: A Subway Train
What are the magnitude and sign of displacements for the motions of the subway train shown in parts (a) and (b) of Figure 10.7?
Strategy
A drawing with a coordinate system is already provided, so we don’t need to make a sketch, but we should analyze it to make sure we understand what it is showing. Pay particular attention to the coordinate system. To find displacement, we use the equation [latex]\Delta x={x}_{f}-{x}_{0}[/latex]. This is straightforward since the initial and final positions are given.
Solution
- Identify the knowns. In the figure we see that [latex]{x}_{f}=\text{6.70 km}[/latex] and
[latex]{x}_{0}=\text{4.70 km}[/latex] for part (a), and [latex]{x\prime }_{f}=3\text{.75 km}[/latex] and [latex]{x\prime }_{0}=5\text{.25 km}[/latex] for part (b). - Solve for displacement in part (a).
[latex]\Delta x={x}_{f}-{x}_{0}=6\text{.}\text{70 km}-4\text{.}\text{70 km}\text{=}\phantom{\rule{0.20em}{0ex}}\text{+}2\text{.}\text{00 km}[/latex]
- Solve for displacement in part (b).
[latex]\Delta x\prime ={x\prime }_{f}-{x\prime }_{0}=\text{3.75 km}-\text{5.25 km}=-\text{1.50 km}[/latex]
Discussion
The direction of the motion in (a) is to the right and therefore its displacement has a positive sign, whereas motion in (b) is to the left and thus has a negative sign.
Example 10.3: Comparing Distance Traveled with Displacement: A Subway Train
What are the distances traveled for the motions shown in parts (a) and (b) of the subway train in Figure 10.7?
Strategy
To answer this question, think about the definitions of distance and distance traveled, and how they are related to displacement. Distance between two positions is defined to be the magnitude of displacement, which was found in Example 10.2. Distance traveled is the total length of the path traveled between the two positions. (See Displacement.) In the case of the subway train shown in Figure 10.7, the distance traveled is the same as the distance between the initial and final positions of the train.
Solution
- The displacement for part (a) was +2.00 km. Therefore, the distance between the initial and final positions was 2.00 km, and the distance traveled was 2.00 km.
- The displacement for part (b) was [latex]\text{−1.5 km.}[/latex] Therefore, the distance between the initial and final positions was 1.50 km, and the distance traveled was 1.50 km.
Discussion
Distance is a scalar. It has magnitude but no sign to indicate direction.
Example 10.4: Calculating Acceleration: A Subway Train Speeding Up
Suppose the train in Figure 10.7(a) accelerates from rest to 30.0 km/h in the first 20.0 s of its motion. What is its average acceleration during that time interval?
Strategy
It is worth it at this point to make a simple sketch:
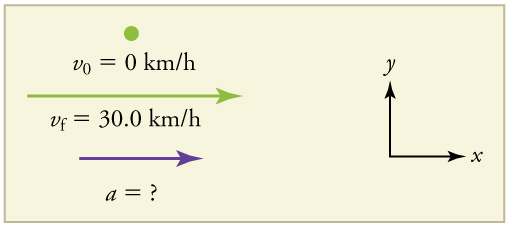
This problem involves three steps. First we must determine the change in velocity, then we must determine the change in time, and finally we use these values to calculate the acceleration.
Solution
- Identify the knowns. [latex]{v}_{0}=0[/latex] (the trains starts at rest), [latex]{v}_{f}=\text{30}\text{.}\text{0 km/h}[/latex], and [latex]\Delta t=\text{20}\text{.}\text{0 s}[/latex].
- Calculate [latex]\Delta v[/latex]. Since the train starts from rest, its change in velocity is [latex]\Delta v\text{=}\phantom{\rule{0.20em}{0ex}}\text{+}\text{30.0 km/h}[/latex], where the plus sign means velocity to the right.
- Plug in known values and solve for the unknown, [latex]\stackrel{-}{a}[/latex].
[latex]\stackrel{-}{a}=\frac{\Delta v}{\Delta t}=\frac{+\text{30.0 km/h}}{\text{20}\text{.}0 s}[/latex]
- Since the units are mixed (we have both hours and seconds for time), we need to convert everything into SI units of meters and seconds. (See Physical Quantities and Units for more guidance.)
[latex]\stackrel{-}{a}=\left(\frac{+\text{30 km/h}}{\text{20.0 s}}\right)\left(\frac{{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{m}}{\text{1 km}}\right)\left(\frac{\text{1 h}}{\text{3600 s}}\right)=0\text{.}{\text{417 m/s}}^{2}[/latex]
Discussion
The plus sign means that acceleration is to the right. This is reasonable because the train starts from rest and ends up with a velocity to the right (also positive). So acceleration is in the same direction as the change in velocity, as is always the case.
Example 10.5: Calculate Acceleration: A Subway Train Slowing Down
Now suppose that at the end of its trip, the train in Figure 10.7(a) slows to a stop from a speed of 30.0 km/h in 8.00 s. What is its average acceleration while stopping?
Strategy

In this case, the train is decelerating and its acceleration is negative because it is toward the left. As in the previous example, we must find the change in velocity and the change in time and then solve for acceleration.
Solution
- Identify the knowns. [latex]{v}_{0}=\text{30}\text{.0 km/h}[/latex], [latex]{v}_{f}=0 km/h[/latex] (the train is stopped, so its velocity is 0), and [latex]\Delta t=\text{8.00 s}[/latex].
- Solve for the change in velocity, [latex]\Delta v[/latex].
[latex]\Delta v={v}_{f}-{v}_{0}=0-\text{30}\text{.}\text{0 km/h}=-\text{30}\text{.0 km/h}[/latex]
- Plug in the knowns, [latex]\Delta v[/latex] and [latex]\Delta t[/latex], and solve for [latex]\stackrel{-}{a}[/latex].
[latex]\stackrel{-}{a}=\frac{\Delta v}{\Delta t}=\frac{-\text{30}\text{.}\text{0 km/h}}{8\text{.}\text{00 s}}[/latex]
- Convert the units to meters and seconds.
[latex]\stackrel{-}{a}=\frac{\Delta v}{\Delta t}=\left(\frac{-\text{30.0 km/h}}{\text{8.00 s}}\right)\left(\frac{{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{m}}{\text{1 km}}\right)\left(\frac{\text{1 h}}{\text{3600 s}}\right)={\text{−1.04 m/s}}^{2}\text{.}[/latex]
Discussion
The minus sign indicates that acceleration is to the left. This sign is reasonable because the train initially has a positive velocity in this problem, and a negative acceleration would oppose the motion. Again, acceleration is in the same direction as the change in velocity, which is negative here. This acceleration can be called a deceleration because it has a direction opposite to the velocity.
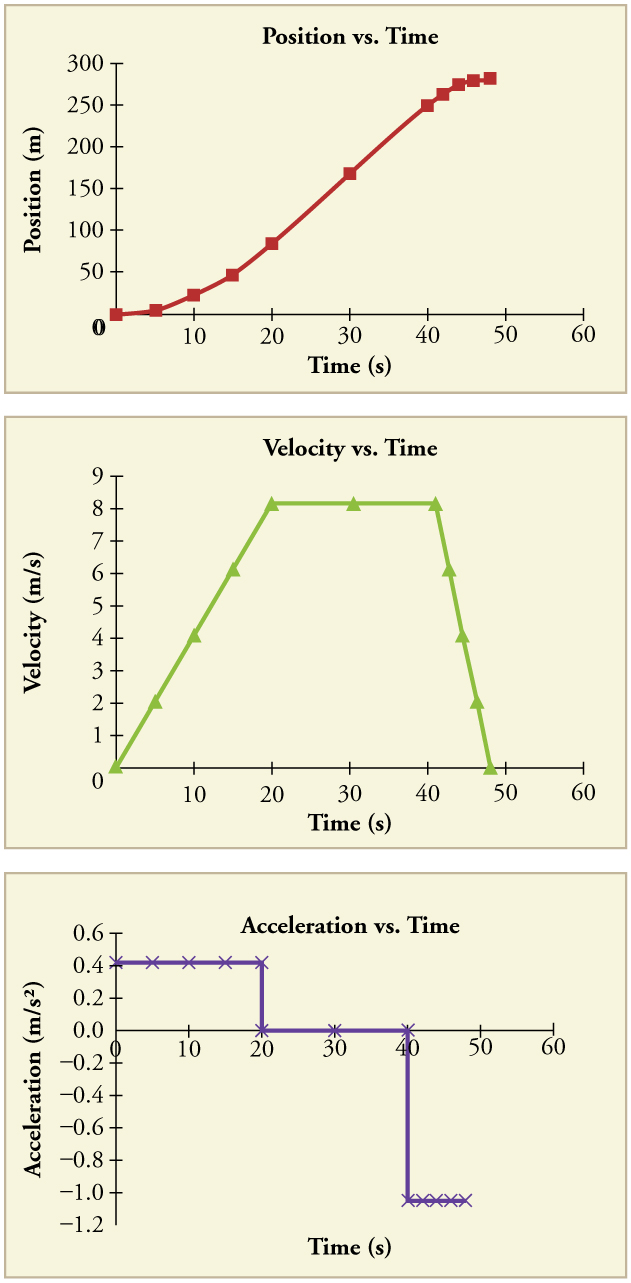
The graphs of position, velocity, and acceleration vs. time for the trains in Example 10.4 and Example 10.5 are displayed in Figure 10.10. (We have taken the velocity to remain constant from 20 to 40 s, after which the train decelerates.)
Example 10.6: Calculating Average Velocity: The Subway Train
What is the average velocity of the train in part b of Example 10.2, and shown again below, if it takes 5.00 min to make its trip?
Strategy
Average velocity is displacement divided by time. It will be negative here, since the train moves to the left and has a negative displacement.
Solution
- Identify the knowns. [latex]{x\prime }_{f}=3\text{.75 km}[/latex], [latex]{x\prime }_{0}=\text{5.25 km}[/latex], [latex]\Delta t=\text{5.00 min}[/latex].
- Determine displacement, [latex]\Delta x\prime[/latex]. We found [latex]\Delta x\prime[/latex] to be [latex]-\text{1.5 km}[/latex] in Example 10.2
- Solve for average velocity.
[latex]\stackrel{-}{v}=\frac{\Delta x\prime }{\Delta t}=\frac{-\text{1.50 km}}{\text{5.00 min}}[/latex]
- Convert units.
[latex]\stackrel{-}{v}=\frac{\Delta x\prime }{\Delta t}=\left(\frac{-1\text{.}\text{50 km}}{5\text{.}\text{00 min}}\right)\left(\frac{\text{60 min}}{1 h}\right)=-\text{18}\text{.0 km/h}[/latex]
Discussion
The negative velocity indicates motion to the left.
Example 10.7 Calculating Deceleration: The Subway Train
Finally, suppose the train in Figure 10.11 slows to a stop from a velocity of 20.0 km/h in 10.0 s. What is its average acceleration?
Strategy
Once again, let’s draw a sketch:

As before, we must find the change in velocity and the change in time to calculate average acceleration.
Solution
- Identify the knowns. [latex]{v}_{0}=-\text{20 km/h}[/latex], [latex]{v}_{f}=0 km/h[/latex], [latex]\Delta t=\text{10}\text{.}0 s[/latex].
- Calculate [latex]\Delta v[/latex]. The change in velocity here is actually positive, since
[latex]\Delta v={v}_{f}-{v}_{0}=0-(-\text{20}\text{ km/h})=+\text{20}\text{ km/h}[/latex]
- Solve for [latex]\stackrel{-}{a}[/latex].
[latex]\stackrel{-}{a}=\frac{\Delta v}{\Delta t}=\frac{+\text{20}\text{.0 km/h}}{\text{10}\text{.}0 s}[/latex]
- Convert units.
[latex]\stackrel{-}{a}=\left(\frac{+\text{20}\text{.}\text{0 km/h}}{\text{10}\text{.}\text{0 s}}\right)\left(\frac{{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}m}{1 km}\right)\left(\frac{1 h}{\text{3600 s}}\right)\text{=}\phantom{\rule{0.25em}{0ex}}\text{+}0\text{.556 m}{\text{/s}}^{2}[/latex]
Discussion
The plus sign means that acceleration is to the right. This is reasonable because the train initially has a negative velocity (to the left) in this problem and a positive acceleration opposes the motion (and so it is to the right). Again, acceleration is in the same direction as the change in velocity, which is positive here. As in Example 10.5, this acceleration can be called a deceleration since it is in the direction opposite to the velocity.
Sign and Direction
Understanding the signs of physical quantities is crucial when analyzing motion. In the coordinate system we’ve adopted, a positive sign (plus) indicates motion to the right, and a negative sign (minus) indicates motion to the left. This is intuitive for displacement and velocity, but less so for acceleration.
Many people associate negative acceleration with slowing down. However, that’s not always true. What matters is whether the acceleration and velocity have the same or opposite signs.
-
If acceleration and velocity have the same sign, the object is speeding up.
-
If they have opposite signs, the object is slowing down.
For example, in a situation like Figure 10.11, a train moving to the left has a negative velocity. If it accelerates to the left (also negative acceleration), its speed increases. This shows that negative acceleration can correspond to speeding up, not slowing down. Conversely, if a train is moving left but experiences positive acceleration (to the right), it would slow down.
This is why interpreting signs based on direction, not just on magnitude, is essential in physics.
Check Your Understanding
Question: An airplane lands on a runway traveling east. Describe its acceleration.
Answer: If east is defined as positive, the airplane’s acceleration is negative—it points west as the plane slows down. Since its acceleration is opposite to its velocity, the airplane is decelerating.
PhET Explorations: Moving Man Simulation
Learn about position, velocity, and acceleration graphs. Move the little man back and forth with the mouse and plot his motion. Set the position, velocity, or acceleration and let the simulation move the man for you.
Figure 10.13: Moving Man.
Section Summary
-
Acceleration is the rate at which velocity changes. In symbols, the average acceleration [latex]\overline{a}[/latex] is given by:
[latex]\overline{a} = \frac{\Delta v}{\Delta t} = \frac{v_f - v_0}{t_f - t_0}[/latex]
-
The SI unit for acceleration is [latex]\text{m/s}^2[/latex] (meters per second squared).
-
Acceleration is a vector, meaning it has both magnitude and direction.
-
Acceleration can result from a change in the magnitude of velocity (speeding up or slowing down), a change in direction, or both.
-
Instantaneous acceleration [latex]a[/latex] is the acceleration at a specific instant in time.
-
Deceleration refers to acceleration that is in the opposite direction to the object's velocity; it causes the object to slow down.
Conceptual Questions
- Is it possible for speed to be constant while acceleration is not zero? Give an example of such a situation.
- Is it possible for velocity to be constant while acceleration is not zero? Explain.
- Give an example in which velocity is zero yet acceleration is not.
- If a subway train is moving to the left (has a negative velocity) and then comes to a stop, what is the direction of its acceleration? Is the acceleration positive or negative?
- Plus and minus signs are used in one-dimensional motion to indicate direction. What is the sign of an acceleration that reduces the magnitude of a negative velocity? Of a positive velocity?
Problems & Exercises
- A cheetah can accelerate from rest to a speed of 30.0 m/s in 7.00 s. What is its acceleration?
- Professional Application Dr. John Paul Stapp was U.S. Air Force officer who studied the effects of extreme deceleration on the human body. On December 10, 1954, Stapp rode a rocket sled, accelerating from rest to a top speed of 282 m/s (1015 km/h) in 5.00 s, and was brought jarringly back to rest in only 1.40 s! Calculate his (a) acceleration and (b) deceleration. Express each in multiples of [latex]g[/latex] [latex]\left(9\text{.}\text{80 m}{\text{/s}}^{2}\right)[/latex] by taking its ratio to the acceleration of gravity.
- A commuter backs her car out of her garage with an acceleration of [latex]1\text{.}{\text{40 m/s}}^{2}[/latex].
- How long does it take her to reach a speed of 2.00 m/s?
- If she then brakes to a stop in 0.800 s, what is her deceleration?
- Assume that an intercontinental ballistic missile goes from rest to a suborbital speed of 6.50 km/s in 60.0 s (the actual speed and time are classified). What is its average acceleration in [latex]{\text{m/s}}^{2}[/latex] and in multiples of [latex]g[/latex] [latex]\left(9\text{.}\text{80 m}{\text{/s}}^{2}\right)?[/latex]
Glossary
- acceleration
- the rate of change in velocity; the change in velocity over time
- average acceleration
- the change in velocity divided by the time over which it changes
- instantaneous acceleration
- acceleration at a specific point in time
- deceleration
- acceleration in the direction opposite to velocity; acceleration that results in a decrease in velocity
The rate of change in velocity; the change in velocity over time
the change in velocity divided by the time over which it changes
acceleration in the direction opposite to velocity; acceleration that results in a decrease in velocity
acceleration at a specific point in time

