"

Oscillatory Motion and Waves and Physics of Hearing.

132 Sound Interference and Resonance: Standing Waves in Air Columns

Learning Objectives

  • Define antinode, node, fundamental, overtones, and harmonics.
  • Identify examples of sound interference in everyday situations.
  • Describe how interference in open and closed tubes affects sound characteristics and musical instrument design.
  • Calculate the length of a resonating tube using sound wave measurements.
Photograph of a pair of headphones and the jack used to connect it to the sound system.
Figure 132.1: Some headphones use constructive and destructive interference to cancel out outside noise. (credit: JVC America, Flickr)

All waves, including sound waves, exhibit interference. This property—constructive and destructive interference—is a defining feature of wave behavior. Interference patterns offer strong evidence that a phenomenon is indeed wave-like. For sound, we’ve already seen interference effects in phenomena such as beats generated by two similar frequencies.

Figure 132.2 demonstrates an application of destructive interference in active noise-canceling headphones. These systems use electronics to generate a second sound wave that is the mirror image of the unwanted noise. The pressure variations of the original and the canceling sound waves combine to reduce the overall pressure variation, thereby lowering the sound intensity. This technique can reduce noise levels by over 30 dB.

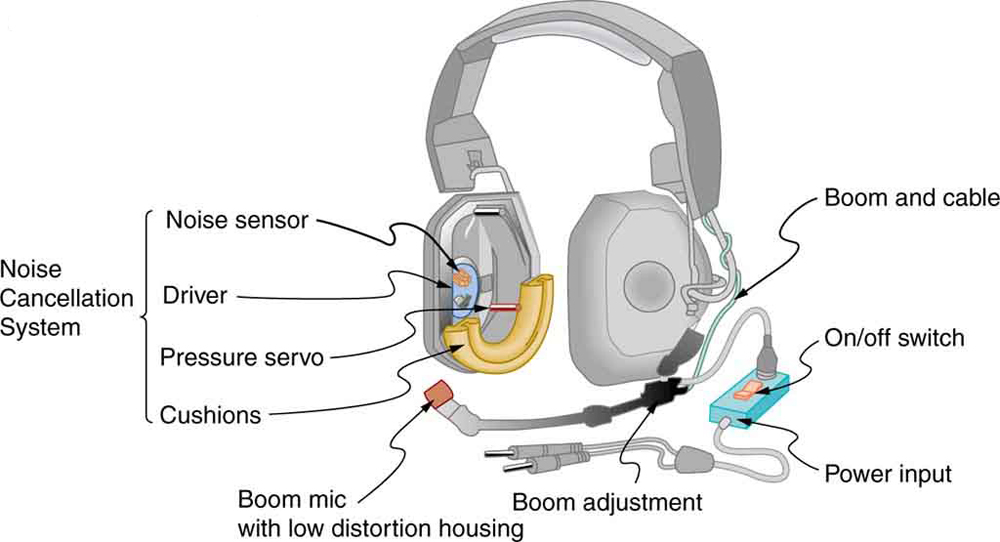
A detailed picture of headphones with all its parts labeled. It shows the noise cancellation system in both the ear plugs consisting of the noise sensor, driver, pressure servo and cushions. There is a boom mic with low frequency housing, a boom adjustment, boom and cable all attached to one side of the power input cable. The power input cable is shown to have an on/off switch.
Figure 132.2: Headphones using destructive interference to cancel noise. The system generates a sound wave that is the inverse of incoming noise, greatly reducing sound intensity.

We also observe interference in musical instruments. All resonances in instruments are the result of interference. Constructive interference forms standing waves at resonant frequencies, while destructive interference suppresses all others. From blowing across a bottle to the acoustics of a violin body, interference is central to sound production and timbre.

Interference

Interference is so fundamental to wave behavior that observing it confirms a phenomenon is wave-like. Light and even electrons have demonstrated interference, reinforcing their wave-particle duality.

Now, consider placing a vibrating tuning fork near one end of a tube closed at the other end, as shown in Figure 132.3, Figure 132.4, Figure 132.5, and Figure 132.6. If the tube’s length corresponds to a resonant frequency, the air column will vibrate strongly. The incoming sound wave reflects at the closed end and interferes with the ongoing wave. If this interference is constructive, a standing wave forms.

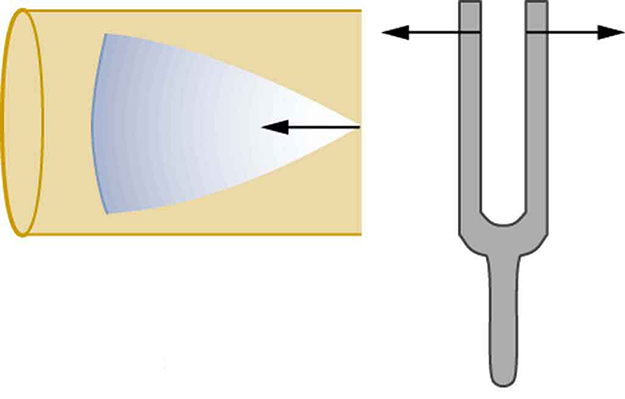
The right side shows a vibrating tuning fork with right arm of fork moving right and left arm moving left. The left side shows a cone of resonance waves moving across a tube from the open end to the closed end. The tip of the cone is at the open end of the tube.
Figure 132.3: A disturbance from a tuning fork travels down a tube closed at one end.
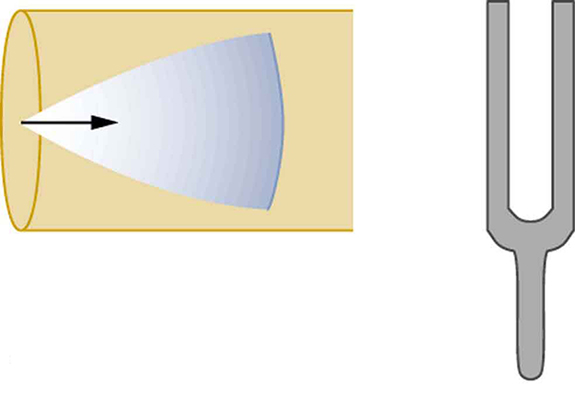
The right side shows a vibrating tuning fork. The left side shows a cone of resonance waves reflected at the closed end of the tube. The tip of the cone is at the closed end of the tube, and the mouth of the cone is moving toward the open end of the tube.
Figure 132.4: The wave reflects from the closed end of the tube.
The left side shows a cone of resonance waves reflected at the closed end of the tube. The mouth of the cone has reached the open end of the tube The right side shows a vibrating tuning fork with its left arm of fork moving rightward and its right arm moving leftward.
Figure 132.5: If the tube’s length is correct, the reflected wave arrives half a cycle later and reinforces the original sound.
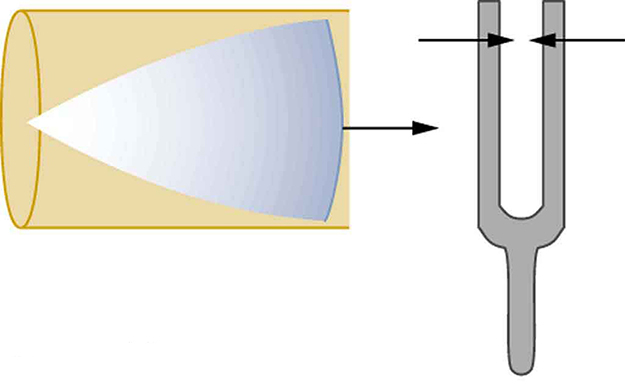
The right side shows a vibrating tuning fork with its right arm moving rightward and left arm moving leftward. The left side shows a cone of resonance waves reflected at the closed end of the tube. The curve side of the cone has reached the tuning fork. The length of the tube is given to be equal to lambda divided by four.
Figure 132.6: The resulting standing wave has a node at the closed end and an antinode at the open end. The tube length corresponds to one-quarter of the wavelength:[latex]\lambda = 4L[/latex]

In a closed-end tube, the displacement is zero at the closed end (node) and maximum at the open end (antinode). This configuration supports a wave where the tube length equals one-quarter of the wavelength.

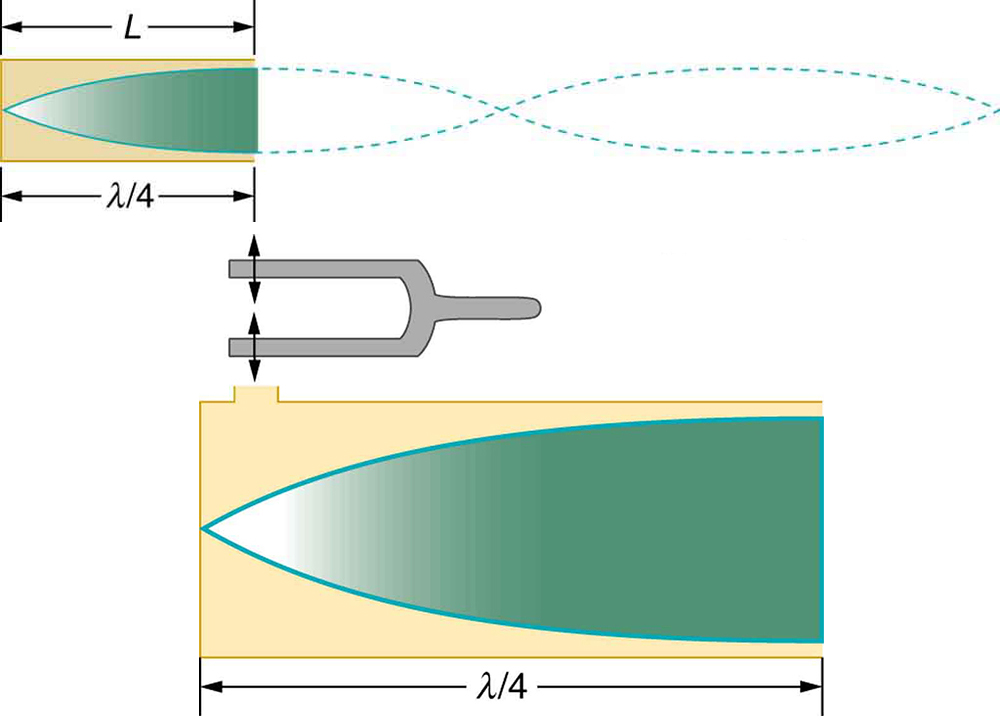
A cone of resonance waves reflected at the closed end of the tube is shown. A tuning fork is shown to vibrate at a small opening above the closed end of the tube. The length of the tube L is given to be equal to lambda divided by four.
Figure 132.7: The same resonance pattern is produced by vibrating air near the closed end of the tube.

Shorter wavelengths can also resonate. Figure 132.8 shows a standing wave with three-fourths of a wavelength inside the tube:

[latex]L = \frac{3}{4} \lambda' \quad \Rightarrow \quad \lambda' = \frac{4L}{3}[/latex]
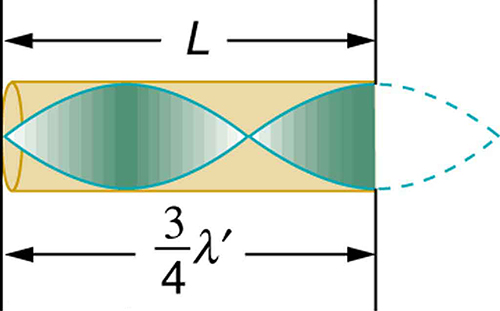
A cone of resonance waves reflected at the closed end of the tube is shown as a wave. There is three-fourth of the wave inside the tube and one-fourth outside shown as dotted curve. The length of the tube is given as three-fourth times lambda prime.
Figure 132.8: First overtone in a tube closed at one end. The wavelength is shorter and the frequency higher.

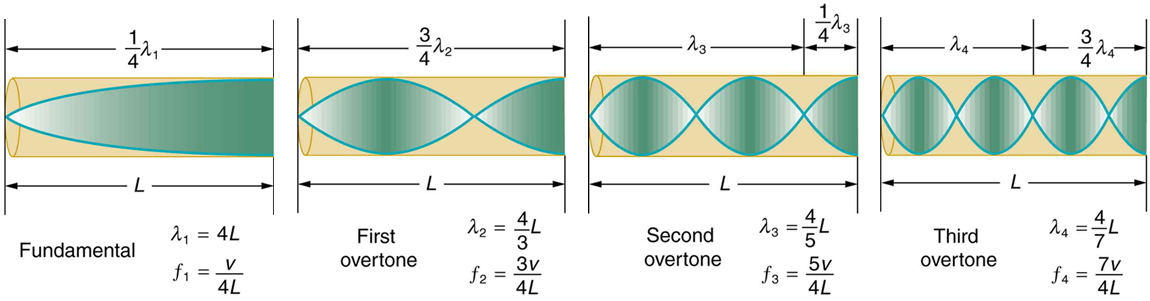
Each resonant frequency is an odd multiple of the fundamental. These frequencies are:

[latex]f_n = n \frac{v_w}{4L}, \quad n = 1, 3, 5, \ldots[/latex]

where [latex]v_w[/latex] is the speed of sound. The fundamental is the first harmonic ([latex]n=1[/latex]), and the overtones are higher harmonics. Figure 132.9 shows the first four resonant frequencies in such a system.

There are four tubes, each of which is closed at one end. Each tube has resonance waves reflected at the closed end. In the first tube, marked Fundamental, the wavelength is long and only one-fourth of the wave is inside the tube, with the maximum air displacement at the open end. In the second tube, marked First overtone, the wavelength is slightly shorter and three-fourths of the wave is inside the tube, with the maximum air displacement at the open end. In the third tube, marked Second overtone, the wavelength is still shorter and one and one-fourth of the wave is inside the tube, with the maximum air displacement at the open end. In the fourth tube, marked Third overtone, the wavelength is shorter than the others, and one and three-fourths of the wave is inside the tube, with the maximum air displacement at the open end.
Figure 132.9: Fundamental and first three overtones for a tube closed at one end. All have a node at the closed end and an antinode at the open end.

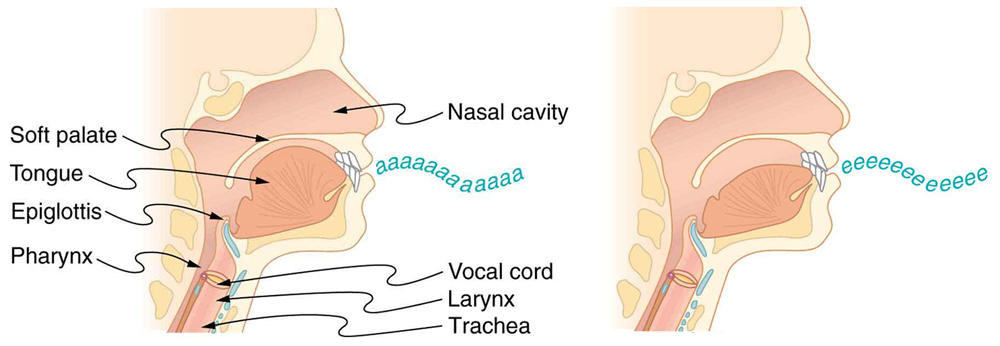
Musical instruments like trumpets and clarinets use these resonant properties to create rich sounds. Though middle C is the same pitch on both instruments, their tone differs due to different overtone combinations and intensities. The same applies to the human voice, where mouth and throat shape modulate the overtone spectrum to produce distinct vowel sounds, as shown in Figure 132.10.

Two pictures of the throat and mouth in cross-section are shown. The first picture has parts of the mouth and throat labeled. The first picture shows the position of the mouth and tongue when producing an a a a sound, and the second picture shows the position of the mouth and tongue when producing an e e e sound.
Figure 132.10: The throat and mouth form a resonating air column closed at one end. Shape and tongue position alter the overtone mix and vowel quality.

Finally, we can express the fundamental frequency mathematically as:

[latex]f = \frac{v_w}{\lambda} = \frac{v_w}{4L}[/latex]

The first overtone is:

[latex]f' = 3 \cdot \frac{v_w}{4L} = 3f[/latex]

Thus, the general pattern of resonant frequencies in a closed-end tube is:

[latex]f_n = n \cdot \frac{v_w}{4L}, \quad \text{for } n = 1, 3, 5, \ldots[/latex]

These resonances depend on temperature, as sound speed increases with temperature. That’s why musicians warm up their wind instruments and why temperature can affect tuning in cold environments like old cathedrals.

Example 132.1: Find the Length of a Tube with a 128 Hz Fundamental

  1. What length should a tube closed at one end have on a day when the air temperature, is [latex]22.0ºC[/latex], if its fundamental frequency is to be 128 Hz (C below middle C)?
  2. What is the frequency of its fourth overtone?

Strategy

The length [latex]L[/latex] can be found from the relationship in [latex]{f}_{n}=n\frac{{v}_{w}}{4L}[/latex], but we will first need to find the speed of sound [latex]{v}_{w}[/latex].

Solution for (a)

  1. Identify knowns:
    • • the fundamental frequency is 128 Hz
    • • the air temperature is [latex]22.0ºC[/latex]
  2. Use [latex]{f}_{n}=n\frac{{v}_{w}}{4L}[/latex] to find the fundamental frequency ([latex]n=1[/latex]).
    [latex]{f}_{1}=\frac{{v}_{w}}{4L}[/latex]
  3. Solve this equation for length.
    [latex]L=\frac{{v}_{w}}{{4f}_{1}}[/latex]
  4. Find the speed of sound using [latex]{v}_{w}=\left(\text{331 m/s}\right)\sqrt{\frac{T}{\text{273 K}}}[/latex] .
    [latex]{v}_{w}=\left(\text{331 m/s}\right)\sqrt{\frac{\text{295 K}}{\text{273 K}}}=\text{344 m/s}[/latex]
  5. Enter the values of the speed of sound and frequency into the expression for [latex]L[/latex].
    [latex]L=\frac{{v}_{w}}{{4f}_{1}}=\frac{\text{344 m/s}}{4\left(\text{128 Hz}\right)}=0\text{.}\text{672 m}[/latex]

Discussion on (a)

Many wind instruments are modified tubes that have finger holes, valves, and other devices for changing the length of the resonating air column and hence, the frequency of the note played. Horns producing very low frequencies, such as tubas, require tubes so long that they are coiled into loops.

Solution for (b)

  1. Identify knowns:
    • • the first overtone has [latex]n=3[/latex]
    • • the second overtone has [latex]n=5[/latex]
    • • the third overtone has [latex]n=7[/latex]
    • • the fourth overtone has [latex]n=9[/latex]
  2. Enter the value for the fourth overtone into [latex]{f}_{n}=n\frac{{v}_{w}}{4L}[/latex].
    [latex]{f}_{9}=9\frac{{v}_{w}}{4L}={9f}_{1}=\text{1.15 kHz}[/latex]

Discussion on (b)

Whether this overtone occurs in a simple tube or a musical instrument depends on how it is stimulated to vibrate and the details of its shape. The trombone, for example, does not produce its fundamental frequency and only makes overtones.

Tubes Open at Both Ends

Another type of tube is one that is open at both ends. Examples include organ pipes, flutes, and oboes. The resonances of tubes open at both ends can be analyzed similarly to those of tubes closed at one end. In these tubes, the air columns have maximum displacement (antinode) at both ends, as illustrated in Figure 132.11. Standing waves form as shown for the fundamental and its overtones.

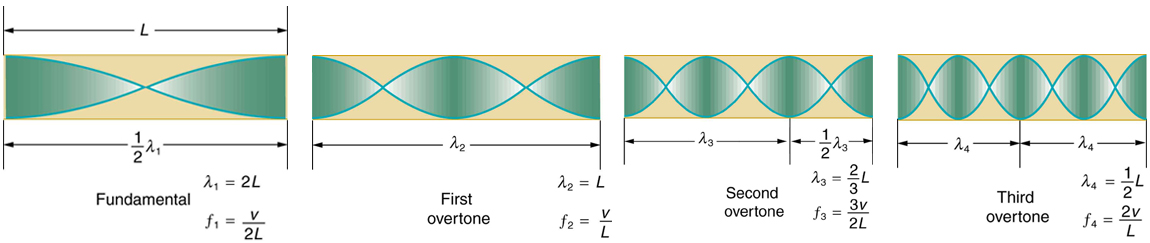
The resonant frequency waves in a tube open at both ends are shown. There are a set of four images. The first image shows a tube of length L marked fundamental having half a wave. The maxima of the vibrations are on both the open ends of the tube. The second image shows a tube of length L marked first over tone having a full wave. The maxima of the vibrations are on both the open ends of the tube. The third image shows a tube of length L marked second over tone having a full wave and a half. The maxima of the vibrations are on both the open ends of the tube. The fourth image shows a tube of length L marked third over tone having two full waves. The maxima of the vibrations are on both the open ends of the tube.
Figure 132.11: The resonant frequencies of a tube open at both ends include the fundamental and the first three overtones. In all cases, the maximum air displacements occur at both ends of the tube, resulting in a different natural frequency structure than that of a closed-end tube.

Since maximum air displacements occur at both ends, the standing wave patterns in an open-open tube have a displacement antinode at each end. Based on this boundary condition and guided by Figure 132.11, the resonant frequencies of a tube open at both ends are given by:

[latex]f_n = n\frac{v_w}{2L}, \quad n = 1, 2, 3, \dots[/latex]

Here, [latex]f_1[/latex] is the fundamental frequency, [latex]f_2[/latex] is the first overtone, and so on. Compared to a closed-end tube of the same length, an open-open tube has a fundamental frequency that is twice as high. It also includes both even and odd multiples of the fundamental in its overtone series, unlike closed tubes, which only contain odd harmonics. Therefore, if you played two tubes with the same fundamental frequency—one open at both ends and one closed at one end—they would sound different. The open tube would sound richer due to its wider overtone spectrum.

Real-World Applications: Resonance in Everyday Systems

Resonance is a common phenomenon in many systems including strings, air columns, and even atomic structures. It is the driven or forced oscillation of a system at its natural frequency. At resonance, energy transfers efficiently, and the amplitude grows until nonlinear effects limit it. An example is the intentionally distorted sound produced in some types of rock music by overdriving the natural resonance of a system.

Sound Amplification Through Resonance

Wind instruments use air column resonance to amplify tones produced by lips or vibrating reeds. Other instruments, like violins and guitars, use sounding boxes to resonate and amplify string vibrations. Figure 132.12 shows how the body of these instruments plays a critical role in shaping their sound. The bridge transmits string vibrations to the body, which resonates and adds overtones to the sound. More complex sounding box shapes allow for resonance across a broader frequency range. The marimba, shown in Figure 132.13, uses gourds as resonance chambers, and their tuning can be adjusted by adding water.

First photograph is of a person playing the guitar and the second photograph is of a violin.
Figure 132.12: String instruments like violins and guitars use resonance in their sounding boxes to amplify and enrich the sound created by vibrating strings. The bridge couples the vibrations to the resonant air in the instrument body. (credits: guitar, Feliciano Guimaraes, Fotopedia; violin, Steve Snodgrass, Flickr)
Photograph of two people playing a marimba with gourds as resonance chambers.
Figure 132.13: The marimba uses gourds as resonance chambers to amplify sound. Resonance has been used in musical instruments since prehistoric times. (credit: APC Events, Flickr)

Although we’ve focused on sound, resonance and standing wave concepts apply to any wave system. For instance, vibrating strings also support fundamental and overtone frequencies. Even atomic orbitals can be interpreted as standing waves of electrons with quantized energy levels. These similarities across physical systems show the universal nature of wave behavior and resonance.

Check Your Understanding

1. Describe how noise-canceling headphones differ from standard headphones used to block outside sounds.

Solution: Regular headphones block external sound with a physical barrier. Noise-canceling headphones use destructive interference to cancel out sound waves by producing an inverted version of the incoming noise.

2. How is it possible to use a standing wave’s node and antinode to determine the length of a closed-end tube?

Solution: In resonance, the node is at the closed end and the antinode is at the open end. This corresponds to one-quarter of a wavelength. So if you know the wave’s wavelength, the tube’s length can be calculated using [latex]L = \frac{\lambda}{4}[/latex].

PhET Explorations: Sound

This simulation lets you visualize sound waves. You can adjust the frequency and amplitude, observe changes in the waveform, and even move the listener to hear different effects.

 

Section Summary

  • Sound interference and resonance follow general wave properties.
  • The lowest-frequency resonance in an air column is the fundamental; higher resonances are overtones, and together they form the harmonic series.
  • The resonant frequencies of a tube closed at one end are:
    [latex]f_n = n\frac{v_w}{4L}, \quad n = 1, 3, 5, \dots[/latex]
  • The resonant frequencies of a tube open at both ends are:
    [latex]f_n = n\frac{v_w}{2L}, \quad n = 1, 2, 3, \dots[/latex]

Conceptual Questions

  1. How does an unamplified guitar produce sounds so much more intense than those of a plucked string held taut by a simple stick?
  2. You are given two wind instruments of identical length. One is open at both ends, whereas the other is closed at one end. Which is able to produce the lowest frequency?
  3. What is the difference between an overtone and a harmonic? Are all harmonics overtones? Are all overtones harmonics?

Problems & Exercises

  1. A “showy” custom-built car has two brass horns that are supposed to produce the same frequency but actually emit 263.8 and 264.5 Hz. What beat frequency is produced?
  2. What beat frequencies will be present: (a) If the musical notes A and C are played together (frequencies of 220 and 264 Hz)? (b) If D and F are played together (frequencies of 297 and 352 Hz)? (c) If all four are played together?
  3. What beat frequencies result if a piano hammer hits three strings that emit frequencies of 127.8, 128.1, and 128.3 Hz?
  4. A piano tuner hears a beat every 2.00 s when listening to a 264.0-Hz tuning fork and a single piano string. What are the two possible frequencies of the string?
  5. (a) What is the fundamental frequency of a 0.672-m-long tube, open at both ends, on a day when the speed of sound is 344 m/s? (b) What is the frequency of its second harmonic?
  6. If a wind instrument, such as a tuba, has a fundamental frequency of 32.0 Hz, what are its first three overtones? It is closed at one end. (The overtones of a real tuba are more complex than this example, because it is a tapered tube.)
  7. What are the first three overtones of a bassoon that has a fundamental frequency of 90.0 Hz? It is open at both ends. (The overtones of a real bassoon are more complex than this example, because its double reed makes it act more like a tube closed at one end.)
  8. How long must a flute be in order to have a fundamental frequency of 262 Hz (this frequency corresponds to middle C on the evenly tempered chromatic scale) on a day when air temperature is [latex]20.0ºC[/latex]? It is open at both ends.
  9. What length should an oboe have to produce a fundamental frequency of 110 Hz on a day when the speed of sound is 343 m/s? It is open at both ends.
  10. What is the length of a tube that has a fundamental frequency of 176 Hz and a first overtone of 352 Hz if the speed of sound is 343 m/s?
  11. (a) Find the length of an organ pipe closed at one end that produces a fundamental frequency of 256 Hz when air temperature is [latex]18.0ºC[/latex]. (b) What is its fundamental frequency at [latex]25.0ºC[/latex]?
  12. By what fraction will the frequencies produced by a wind instrument change when air temperature goes from [latex]10.0ºC[/latex] to [latex]30.0ºC[/latex]? That is, find the ratio of the frequencies at those temperatures.
  13. The ear canal resonates like a tube closed at one end. (See Chapter 17.6 The Hearing Mechanism.) If ear canals range in length from 1.80 to 2.60 cm in an average population, what is the range of fundamental resonant frequencies? Take air temperature to be [latex]37.0ºC[/latex], which is the same as body temperature. How does this result correlate with the intensity versus frequency graph (Figure 132.3 of the human ear?
  14. Calculate the first overtone in an ear canal, which resonates like a 2.40-cm-long tube closed at one end, by taking air temperature to be [latex]37.0ºC[/latex]. Is the ear particularly sensitive to such a frequency? (The resonances of the ear canal are complicated by its nonuniform shape, which we shall ignore.)
  15. A crude approximation of voice production is to consider the breathing passages and mouth to be a resonating tube closed at one end. (See Figure 132.10.) (a) What is the fundamental frequency if the tube is 0.240-m long, by taking air temperature to be [latex]37.0ºC[/latex]? (b) What would this frequency become if the person replaced the air with helium? Assume the same temperature dependence for helium as for air.
  16. (a) Students in a physics lab are asked to find the length of an air column in a tube closed at one end that has a fundamental frequency of 256 Hz. They hold the tube vertically and fill it with water to the top, then lower the water while a 256-Hz tuning fork is rung and listen for the first resonance. What is the air temperature if the resonance occurs for a length of 0.336 m? (b) At what length will they observe the second resonance (first overtone)?
  17. What frequencies will a 1.80-m-long tube produce in the audible range at [latex]20.0ºC[/latex] if: (a) The tube is closed at one end? (b) It is open at both ends?

Glossary

antinode
point of maximum displacement
node
point of zero displacement
fundamental
the lowest-frequency resonance
overtones
all resonant frequencies higher than the fundamental
harmonics
the term used to refer collectively to the fundamental and its overtones
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book