The familiar sound of a motorcycle zooming past—starting with a high-pitched whine that drops suddenly to a low-pitched roar—is a common example of the Doppler effect. The faster the motorcycle, and the closer it passes by the listener, the more noticeable the pitch change. We hear this same effect with passing race cars, trains, and airplanes. The Doppler effect is so common that it is often mimicked in play to represent movement.

The Doppler effect refers to the change in the frequency of a sound as perceived by an observer due to motion of either the sound source or the observer. When the source or observer is moving, the observed frequency differs from the emitted frequency. This change is called a Doppler shift. Though commonly associated with moving sources, the effect is also apparent when a stationary sound source is heard by a moving observer. For instance, when riding a train past a ringing bell, the pitch of the bell appears higher as you approach and lower as you move away.

This phenomenon was first studied by Austrian physicist Christian Johann Doppler (1803–1853), who conducted experiments involving musicians performing on moving train cars and on the ground. Observers measured changes in pitch depending on their location relative to the motion of the sound source.

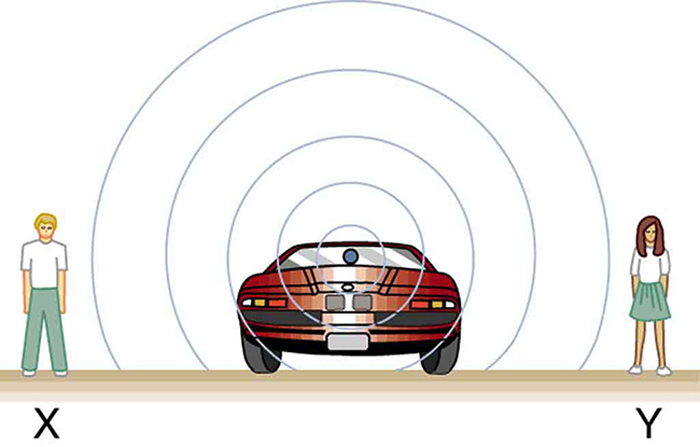
Figures 131.1, 131.2, and 131.3 illustrate how sound waves behave differently for stationary versus moving sources and observers. In Figure 131.1, the source, observers, and air are all stationary, so the sound waves are evenly spaced in all directions, and both observers hear the same frequency.

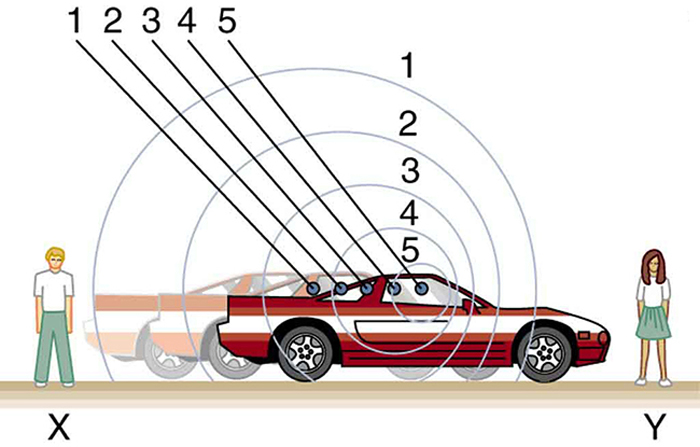
In Figure 131.2, the source is moving to the right. Each compression of air is emitted from a point that keeps changing position, resulting in compressed waves ahead of the source (shorter wavelength and higher frequency) and spread-out waves behind it (longer wavelength and lower frequency). As a result, the observer in front of the moving source hears a higher-pitched sound, while the one behind hears a lower pitch.

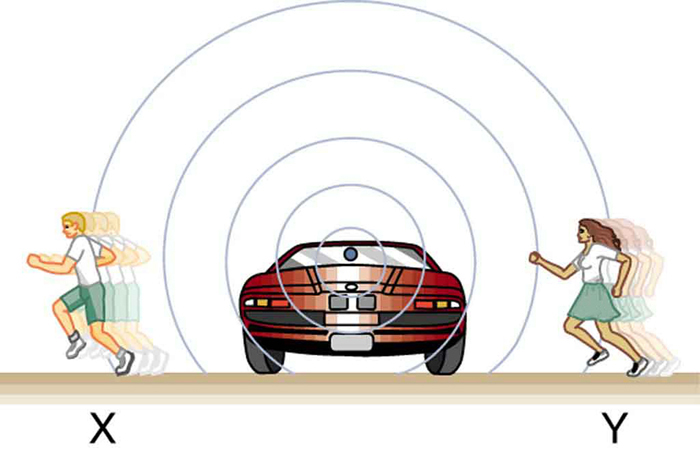
Figure 131.3 shows the effect of motion by the observer rather than the source. The observer moving toward a stationary source encounters wavefronts more frequently, hearing a higher frequency. In contrast, an observer moving away encounters fewer wavefronts per second and hears a lower pitch.

Since the speed of sound [latex]v_w[/latex] is constant in a given medium, a change in perceived wavelength implies a change in perceived frequency. Thus, motion toward a source compresses the wavelength and increases the observed frequency. Motion away stretches the wavelength and lowers the observed frequency. The faster the relative motion, the larger the frequency shift.

For a stationary observer and a moving source, the observed frequency [latex]f_{\text{obs}}[/latex] is given by:

Here, [latex]f_s[/latex] is the frequency emitted by the source, [latex]v_s[/latex] is the speed of the source, and [latex]v_w[/latex] is the speed of sound. Use the minus sign when the source moves toward the observer (increasing frequency), and the plus sign when it moves away (decreasing frequency).

For a stationary source and a moving observer, the observed frequency is:

In this case, [latex]v_{\text{obs}}[/latex] is the speed of the observer. Use the plus sign if the observer moves toward the source (hearing a higher frequency), and the minus sign if moving away (hearing a lower frequency).

Sonic Booms to Bow Wakes

What happens when a source of sound, like a jet aircraft, moves toward or even faster than the speed of sound? This question has implications not just for sound but for all types of waves.

Suppose a jet plane is flying nearly directly toward a listener while emitting sound at frequency [latex]f_s[/latex]. As the plane’s speed [latex]v_s[/latex] increases, the Doppler shift increases, and the observed frequency [latex]f_{\text{obs}}[/latex] becomes greater. The formula for the Doppler effect is:

[latex]f_{\text{obs}} = f_s \left( \frac{v_w}{v_w \pm v_s} \right)[/latex]

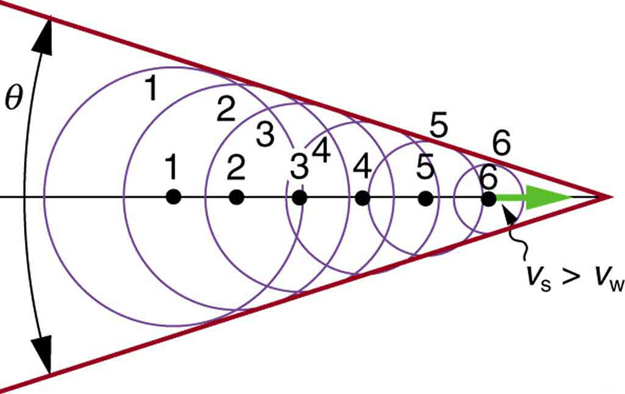
As the speed of the source [latex]v_s[/latex] approaches the speed of sound [latex]v_w[/latex], the denominator approaches zero, and the observed frequency theoretically approaches infinity. Physically, this means that each successive sound wave is emitted from the same point in space as the previous one, stacking up and forming a large pressure front. When the source breaks the sound barrier, this pressure front becomes a shock wave, and the listener experiences a sonic boom. (See Figure 131.4.)

In three dimensions, the sound waves form a cone behind the moving object. Along the surface of this cone, constructive interference occurs, forming a sharp and intense sound wave—the sonic boom. Inside the cone, interference is mostly destructive, resulting in quieter regions. An aircraft typically produces two sonic booms: one from the nose and one from the tail. These can be heard as two distinct booms by an observer on the ground, separated by the time it takes the aircraft to pass overhead. (See Figure 131.5.)

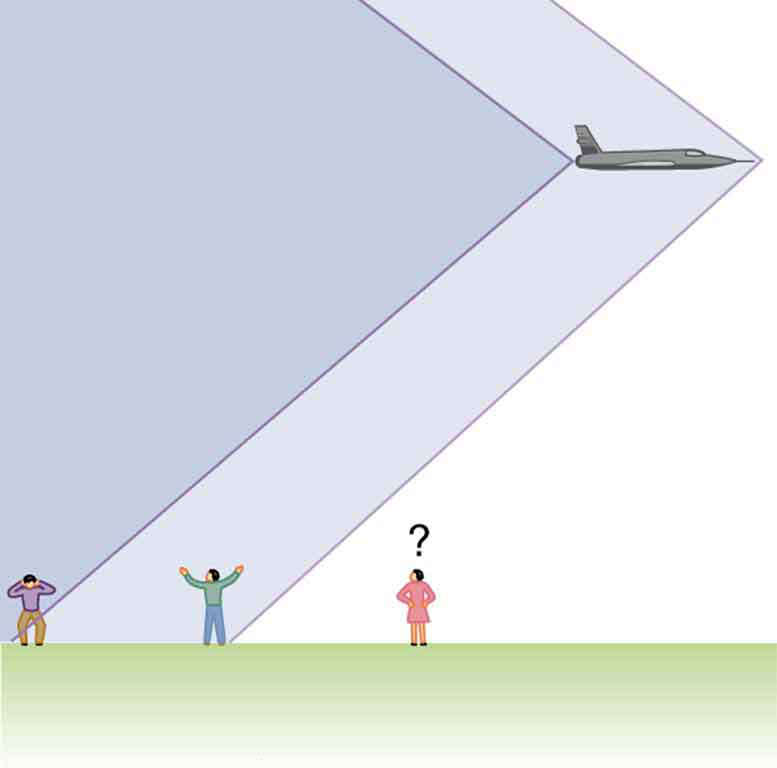
Sonic booms are a specific case of a broader wave phenomenon known as bow wakes. A bow wake is created when any wave source travels faster than the wave speed in the medium. A familiar example is the V-shaped wake behind a duck swimming through water faster than wave ripples can spread. (See Figure 131.6.)

Bow wakes aren’t limited to sound or water. In particle physics, a subatomic particle moving faster than the speed of light in a medium (such as water) creates a visual analog to the sonic boom, called Cerenkov radiation. This radiation appears as a cone of blue light, often observed in nuclear reactors. (See Figure 131.7.)

Both Doppler shifts and sonic booms are important phenomena with a wide range of practical applications. For example, the Doppler shift is used in:

• Medical imaging, such as Doppler ultrasound to measure blood flow velocity
• Law enforcement radar to determine vehicle speeds
• Meteorology, to track the velocity of weather systems using Doppler radar
• Astronomy, to determine the speed and direction of distant galaxies based on the red shift of light, helping estimate the age of the universe

Check Your Understanding

Why did scientist Christian Doppler observe musicians both on a moving train and also from a stationary point not on the train?

Doppler needed to compare the perception of sound when the observer is stationary and the source moves, and vice versa. This helped him understand how relative motion affects observed frequency.

Check Your Understanding

Describe a situation in your life when you might rely on the Doppler shift to help you either while driving a car or walking near traffic.

If I hear the pitch of a siren rising as an ambulance approaches while driving, I know to prepare to pull over. The Doppler shift helps me tell whether the vehicle is approaching or has passed.

Section Summary

• The Doppler effect is a change in observed sound frequency due to motion of the source or observer.
• The change in frequency is called the Doppler shift.
• A sonic boom is a shock wave formed by constructive interference when a source travels faster than sound.
• Sonic booms are a specific type of bow wake, which occurs when any wave source exceeds the wave speed in the medium.
• For a stationary observer and moving source:
  [latex]f_{\text{obs}} = f_s \left( \frac{v_w}{v_w \pm v_s} \right)[/latex]
• For a stationary source and moving observer:
  [latex]f_{\text{obs}} = f_s \left( \frac{v_w \pm v_{\text{obs}}}{v_w} \right)[/latex]