Oscillatory Motion and Waves and Physics of Hearing.
129 Speed of Sound, Frequency, and Wavelength
Learning Objectives
- Define pitch.
- Describe the relationship between the speed of sound, its frequency, and its wavelength.
- Describe how different media affect the speed of sound.
- Explain how temperature influences the speed of sound.

Sound, like all waves, travels at a specific speed and exhibits the properties of frequency and wavelength. You can observe this during a fireworks display: the bright flash appears before the sound reaches you. This delay shows that sound travels at a finite speed and is much slower than light.
Our perception of a sound’s frequency is called pitch. While we don’t directly sense a sound’s wavelength, we can observe that small musical instruments (like piccolos) tend to produce high-pitched sounds, which correspond to shorter wavelengths. Larger instruments (like tubas) produce lower-pitched sounds with longer wavelengths.
The relationship between speed, frequency, and wavelength is the same for all waves:
Here, [latex]{v}_{\text{w}}[/latex] is the speed of sound, [latex]f[/latex] is frequency, and [latex]\lambda[/latex] is wavelength. The wavelength is the distance between repeating features of a wave—such as compressions in a sound wave—while frequency is the number of such features passing a point per second.
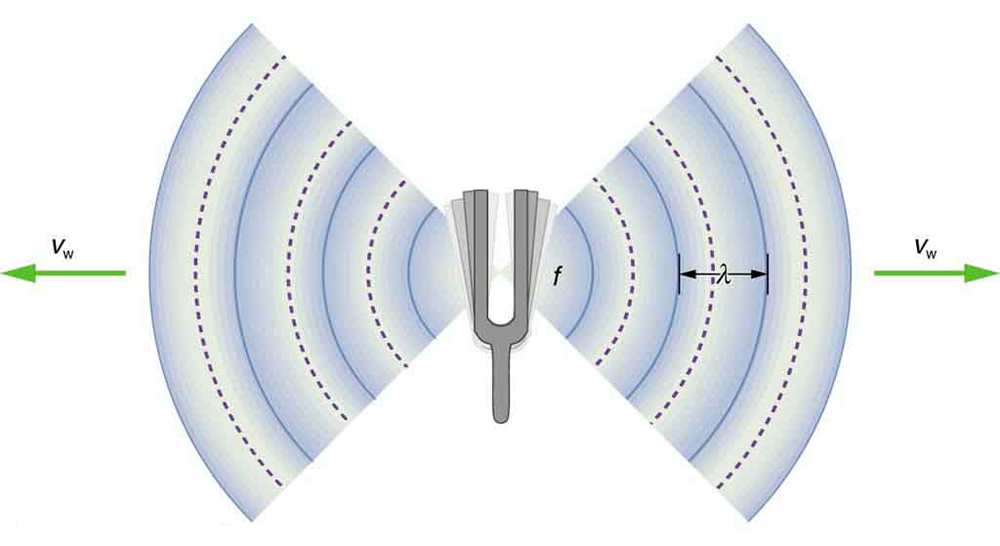
Table 129.1 illustrates how the speed of sound depends on the medium. Sound travels faster in more rigid (less compressible) materials and slower in denser materials. That’s why sound moves faster in solids than in gases.
Earthquakes provide a real-world example of these principles. Seismic waves traveling through Earth’s crust include both longitudinal (P-waves) and transverse (S-waves). In granite, the speed of P-waves is much higher than that of S-waves, due to differences in material rigidity. These wave speeds help seismologists determine the location of an earthquake’s epicenter.Temperature also affects the speed of sound, especially in gases. For air, the relationship is approximately:
Here, [latex]T[/latex] is the absolute temperature in kelvins. This equation shows that sound travels faster at higher temperatures. The reason lies in molecular motion—faster-moving particles transmit sound more quickly.
This relationship can also be tied to the root-mean-square (rms) speed of gas molecules:
where [latex]k[/latex] is the Boltzmann constant and [latex]m[/latex] is the mass of a gas particle. This supports the idea that sound speed in gases increases with temperature.
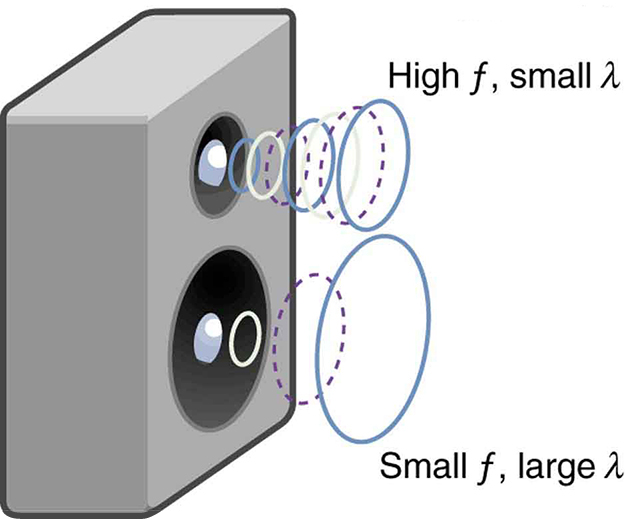
Importantly, the speed of sound is nearly independent of frequency. This means that both low- and high-pitch sounds travel at nearly the same speed in air. If this were not the case, you’d hear musical instruments in a marching band arrive out of sync. Since the wave speed [latex]{v}_{\text{w}}[/latex] is constant for a given medium, a higher frequency implies a shorter wavelength:
Example 129.1: Calculating Wavelengths: What Are the Wavelengths of Audible Sounds?
Calculate the wavelengths of sounds at the extremes of the audible range, 20 and 20,000 Hz, in
[latex]\text{30.0ºC}[/latex] air. (Assume that the frequency values are accurate to two significant figures.)
Strategy
To find wavelength from frequency, we can use [latex]{v}_{\text{w}}=\mathrm{f\lambda }[/latex].
Solution
- Identify knowns. The value for [latex]{v}_{\text{w}}[/latex], is given by
[latex]{v}_{\text{w}}=\left(\text{331}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)\sqrt{\frac{T}{\text{273}\phantom{\rule{0.25em}{0ex}}\text{K}}}.[/latex]
- Convert the temperature into kelvin and then enter the temperature into the equation
[latex]{v}_{\text{w}}=\left(\text{331}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)\sqrt{\frac{\text{303 K}}{\text{273}\phantom{\rule{0.25em}{0ex}}\text{K}}}=\text{348}\text{.}7\phantom{\rule{0.25em}{0ex}}\text{m/s}.[/latex]
- Solve the relationship between speed and wavelength for [latex]\lambda[/latex]:
[latex]\lambda =\frac{{v}_{w}}{f}.[/latex]
- Enter the speed and the minimum frequency to give the maximum wavelength:
[latex]{\lambda }_{\text{max}}=\frac{\text{348}\text{.}7\phantom{\rule{0.25em}{0ex}}\text{m/s}}{\text{20 Hz}}=\text{17}\phantom{\rule{0.25em}{0ex}}\text{m}.[/latex]
- Enter the speed and the maximum frequency to give the minimum wavelength:
[latex]{\lambda }_{\text{min}}=\frac{\text{348}\text{.}7\phantom{\rule{0.25em}{0ex}}\text{m/s}}{\text{20}\text{,}\text{000 Hz}}=0\text{.}\text{017}\phantom{\rule{0.25em}{0ex}}\text{m}=1\text{.}\text{7 cm}.[/latex]
Discussion
Because the product of [latex]f[/latex] multiplied by [latex]\lambda[/latex] equals a constant, the smaller [latex]f[/latex] is, the larger [latex]\lambda[/latex] must be, and vice versa.
The speed of sound changes when sound travels from one medium to another. However, the frequency usually remains the same because the sound acts like a driven oscillation—it retains the frequency of the original source. Since the wave speed [latex]{v}_{\text{w}}[/latex] changes across media but the frequency [latex]f[/latex] does not, the wavelength [latex]\lambda[/latex] must change. That is, because
an increase in wave speed corresponds to a proportional increase in wavelength if the frequency is constant.
Making Connections: Take-Home Investigation—Voice as a Sound Wave
Try suspending a sheet of paper so that the top edge is fixed—tape it to a tabletop, for example—and the bottom edge is free to move. Gently blow near the bottom edge and observe the motion. Then, speak softly and then loudly so the sound waves strike the bottom of the paper. Note the effects of the sound waves. How does the motion of the paper relate to the volume and vibration of your voice?
Check Your Understanding
Imagine you observe two fireworks explode. You hear one explosion at the same moment you see it, but for the second firework, you see the flash several milliseconds before hearing the sound. Why does this occur?
Sound and light travel at different speeds. Light travels significantly faster than sound. For the first firework, the distance is so short that the delay isn’t noticeable. For the second, the greater distance causes a noticeable lag between seeing the flash and hearing the boom.
Check Your Understanding
You observe two musical instruments without hearing them. One produces high-pitch sounds, and the other produces low-pitch sounds. How could you determine which is which?
Compare the sizes of the instruments. High-pitch instruments are generally smaller, as they produce shorter wavelengths. Low-pitch instruments tend to be larger, corresponding to longer wavelengths.
Section Summary
- The speed of sound [latex]{v}_{\text{w}}[/latex], frequency [latex]f[/latex], and wavelength [latex]\lambda[/latex] are related by the wave equation:
[latex]{v}_{\text{w}} = f \lambda[/latex]
This relationship applies to all types of waves.
- In air, the speed of sound depends on temperature [latex]T[/latex] (in kelvins) and is given by:
[latex]{v}_{\text{w}} = (331 \, \text{m/s}) \sqrt{\frac{T}{273 \, \text{K}}}[/latex]
- In a given medium, the speed of sound remains nearly constant across all audible frequencies.
Conceptual Questions
- How do sound vibrations of atoms differ from thermal motion?
- When sound passes from one medium to another where its propagation speed is different, does its frequency or wavelength change? Explain your answer briefly.
Problems & Exercises
- When poked by a spear, an operatic soprano lets out a 1200-Hz shriek. What is its wavelength if the speed of sound is 345 m/s?
- What frequency sound has a 0.10-m wavelength when the speed of sound is 340 m/s?
- Calculate the speed of sound on a day when a 1500 Hz frequency has a wavelength of 0.221 m.
- (a) What is the speed of sound in a medium where a 100-kHz frequency produces a 5.96-cm wavelength? (b) Which substance in Table 129.1 is this likely to be?
- Show that the speed of sound in [latex]\text{20.0ºC}[/latex] air is 343 m/s, as claimed in the text.
- Air temperature in the Sahara Desert can reach [latex]\text{56.0ºC}[/latex] (about [latex]\text{134ºF}[/latex]). What is the speed of sound in air at that temperature
- Dolphins make sounds in air and water. What is the ratio of the wavelength of a sound in air to its wavelength in seawater? Assume air temperature is [latex]\text{20.0ºC}[/latex].
- A sonar echo returns to a submarine 1.20 s after being emitted. What is the distance to the object creating the echo? (Assume that the submarine is in the ocean, not in fresh water.)
- (a) If a submarine’s sonar can measure echo times with a precision of 0.0100 s, what is the smallest difference in distances it can detect? (Assume that the submarine is in the ocean, not in fresh water.) (b) Discuss the limits this time resolution imposes on the ability of the sonar system to detect the size and shape of the object creating the echo.
- A physicist at a fireworks display times the lag between seeing an explosion and hearing its sound, and finds it to be 0.400 s. (a) How far away is the explosion if air temperature is [latex]\text{24.0ºC}[/latex] and if you neglect the time taken for light to reach the physicist? (b) Calculate the distance to the explosion taking the speed of light into account. Note that this distance is negligibly greater.
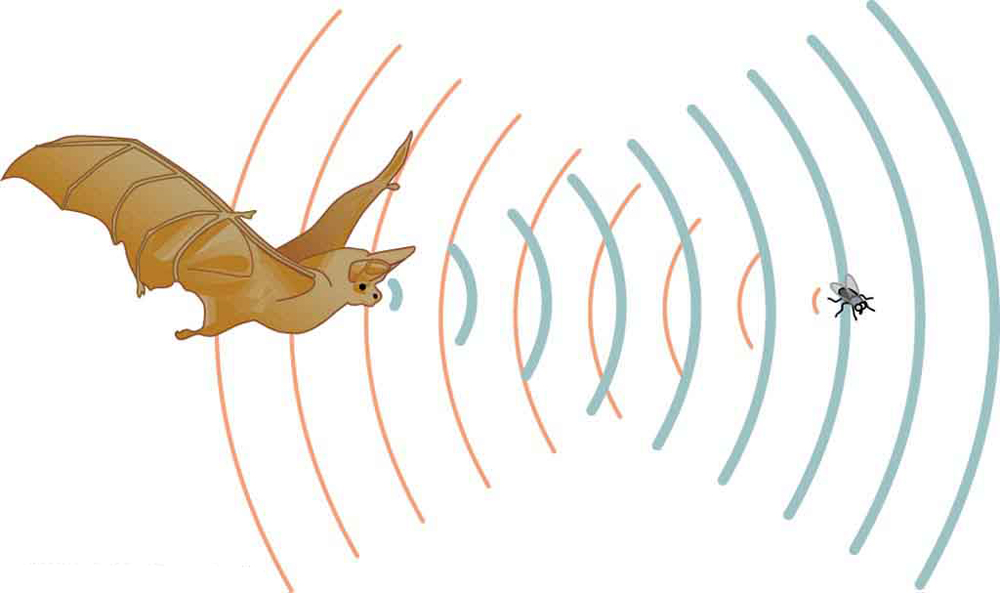
- Suppose a bat uses sound echoes to locate its insect prey, 3.00 m away. (See Figure 129.3.) (a) Calculate the echo times for temperatures of [latex]\text{5.00ºC}[/latex] and [latex]\text{35.0ºC}[/latex]. (b) What percent uncertainty does this cause for the bat in locating the insect? (c) Discuss the significance of this uncertainty and whether it could cause difficulties for the bat. (In practice, the bat continues to use sound as it closes in, eliminating most of any difficulties imposed by this and other effects, such as motion of the prey.)
Glossary
- pitch
- the perception of the frequency of a sound
the perception of the frequency of a sound

