Oscillatory Motion and Waves and Physics of Hearing.
126 Energy in Waves: Intensity
Learning Objectives
- Calculate the intensity and the power of rays and waves.

All waves carry energy. This energy is often visible or measurable in physical, biological, or even physiological systems. For example, seismic waves generated by earthquakes can destroy buildings, while sound waves at high volumes can damage cells in the inner ear and lead to permanent hearing loss. In medicine, ultrasonic waves are used therapeutically to deliver heat deep into tissues to treat muscle injuries, and in diagnostic imaging through ultrasound scans. Laser light, a concentrated electromagnetic wave, can destroy malignant tissue with high precision.
The amount of energy a wave carries is related to its amplitude. A larger-amplitude wave has more energy. In physical systems, a larger displacement requires a stronger restoring force. For example, consider a wave in a stretched spring: stretching the spring further requires more work. Mathematically, the force to produce a displacement [latex]x[/latex] is
where [latex]k[/latex] is the spring constant. The work required to stretch the spring is proportional to [latex]x^2[/latex], and so is the energy stored in the wave:
This means that wave energy is proportional to the square of its amplitude. So doubling the amplitude of a wave quadruples the energy it carries.
But energy also depends on time and area. A short pulse of ultrasound may deliver less total energy than a longer application, even if both have the same amplitude. Likewise, the same total energy spread over a larger area delivers less energy per unit area. For example, focusing sunlight through a magnifying glass can start a fire, while the same sunlight spread over a table is harmless.
Wave Intensity
To quantify how much energy a wave delivers over time and area, we define the intensity [latex]I[/latex] of a wave as the power [latex]P[/latex] delivered per unit area [latex]A[/latex]:
Intensity is measured in watts per square meter ([latex]\text{W/m}^2[/latex]) and applies to all types of wave energy, including sound, light, and seismic activity. For example, solar radiation just above Earth’s atmosphere has an intensity of approximately
This is a substantial amount of power arriving at every square meter of the atmosphere, and it drives Earth’s climate and energy systems.
In acoustics, intensity is often measured using the decibel scale. For instance, a sound level of 90 decibels corresponds to an intensity of
This is already considered loud enough to pose a risk of hearing damage with prolonged exposure. We’ll explore the decibel scale in greater detail in an upcoming chapter.
Example 126.1: Calculating intensity and power: How much energy is in a ray of sunlight?
The average intensity of sunlight on Earth’s surface is about [latex]7\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex].
(a) Calculate the amount of energy that falls on a solar collector having an area of [latex]0\text{.}\text{500}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex] in [latex]4\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{h}[/latex].
(b) What intensity would such sunlight have if concentrated by a magnifying glass onto an area 200 times smaller than its own?
Strategy a
Because power is energy per unit time or [latex]P=\frac{E}{t}[/latex], the definition of intensity can be written as [latex]I=\frac{P}{A}=\frac{E/t}{A}[/latex], and this equation can be solved for E with the given information.
Solution a
- Begin with the equation that states the definition of intensity:
[latex]I=\frac{P}{A}.[/latex]
- Replace [latex]P[/latex] with its equivalent [latex]E/t[/latex]:
[latex]I=\frac{E/t}{A}.[/latex]
- Solve for [latex]E[/latex]:
[latex]E=\text{IAt}.[/latex]
- Substitute known values into the equation:
[latex]E=\left(\text{700}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}\right)\left(0\text{.}\text{500}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}\right)\left[\left(4\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{h}\right)\left(\text{3600}\phantom{\rule{0.25em}{0ex}}\text{s/h}\right)\right].[/latex]
- Calculate to find [latex]E[/latex] and convert units:
[latex]5\text{.}\text{04}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{J},[/latex]
Discussion a
The energy falling on the solar collector in 4 h in part is enough to be useful—for example, for heating a significant amount of water.
Strategy b
Taking a ratio of new intensity to old intensity and using primes for the new quantities, we will find that it depends on the ratio of the areas. All other quantities will cancel.
Solution b
- Take the ratio of intensities, which yields:
[latex]\frac{I\prime }{I}=\frac{P\prime /A\prime }{P/A}=\frac{A}{A\prime }\phantom{\rule{0.25em}{0ex}}\left(\text{The powers cancel because}\phantom{\rule{0.25em}{0ex}}P\prime =P\right)\text{.}[/latex]
- Identify the knowns:
[latex]A=\text{200}A\prime ,[/latex][latex]\frac{I\prime }{I}=\text{200}.[/latex]
- Substitute known quantities:
[latex]I\prime =\text{200}I=\text{200}\left(\text{700}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}\right).[/latex]
- Calculate to find [latex]I\prime[/latex]:
[latex]I\prime =\text{1.40}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}.[/latex]
Discussion b
Decreasing the area increases the intensity considerably. The intensity of the concentrated sunlight could even start a fire.
Example 126.2: Determine the combined intensity of two waves: Perfect constructive interference
If two identical waves, each having an intensity of [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex], interfere perfectly constructively, what is the intensity of the resulting wave?
Strategy
We know from Superposition and Interference that when two identical waves, which have equal amplitudes [latex]X[/latex], interfere perfectly constructively, the resulting wave has an amplitude of [latex]2X[/latex]. Because a wave’s intensity is proportional to amplitude squared, the intensity of the resulting wave is four times as great as in the individual waves.
Solution
- Recall that intensity is proportional to amplitude squared.
- Calculate the new amplitude:
[latex]I\prime \propto {\left(X\prime \right)}^{2}={\left(2X\right)}^{2}={4X}^{2}.[/latex]
- Recall that the intensity of the old amplitude was:
[latex]{I}^{}\propto {X}^{2}.[/latex]
- Take the ratio of new intensity to the old intensity. This gives:
[latex]\frac{I\prime }{I}=4.[/latex]
- Calculate to find [latex]I\prime[/latex]:
[latex]I\prime =4I=4\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}.[/latex]
Discussion
The intensity goes up by a factor of 4 when the amplitude doubles. This answer is a little disquieting. The two individual waves each have intensities of [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex], yet their sum has an intensity of [latex]4\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex], which may appear to violate conservation of energy. This violation, of course, cannot happen. What does happen is intriguing. The area over which the intensity is [latex]4\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex] is much less than the area covered by the two waves before they interfered. There are other areas where the intensity is zero. The addition of waves is not as simple as our first look in Superposition and Interference suggested. We actually get a pattern of both constructive interference and destructive interference whenever two waves are added. For example, if we have two stereo speakers putting out [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex] each, there will be places in the room where the intensity is [latex]4\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex], other places where the intensity is zero, and others in between. Figure 126.2 shows what this interference might look like. We will pursue interference patterns elsewhere in this text.
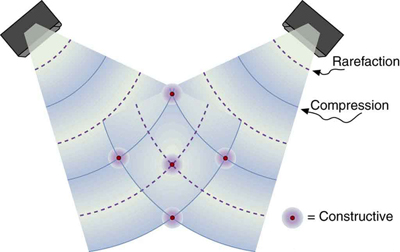
Check Your Understanding
Which measurement of a wave is most important when determining the wave’s intensity?
Amplitude, because a wave’s energy is directly proportional to its amplitude squared.
Section Summary
Intensity is defined to be the power per unit area:
[latex]I=\frac{P}{A}[/latex] and has units of [latex]{\text{W/m}}^{2}[/latex].
Conceptual Questions
- Two identical waves undergo pure constructive interference. Is the resultant intensity twice that of the individual waves? Explain your answer.
- Circular water waves decrease in amplitude as they move away from where a rock is dropped. Explain why.
Problems & Exercises
- Medical Application Ultrasound of intensity [latex]1\text{.}\text{50}×{\text{10}}^{2}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex] is produced by the rectangular head of a medical imaging device measuring 3.00 by 5.00 cm. What is its power output?
- The low-frequency speaker of a stereo set has a surface area of [latex]0\text{.}\text{05}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex] and produces 1W of acoustical power. What is the intensity at the speaker? If the speaker projects sound uniformly in all directions, at what distance from the speaker is the intensity [latex]0\text{.}1\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex]?
- To increase intensity of a wave by a factor of 50, by what factor should the amplitude be increased?
- Engineering Application A device called an insolation meter is used to measure the intensity of sunlight has an area of 100 cm2 and registers 6.50 W. What is the intensity in [latex]{\text{W/m}}^{2}[/latex]?
- Astronomy Application Energy from the Sun arrives at the top of the Earth’s atmosphere with an intensity of [latex]1.30\phantom{\rule{0.25em}{0ex}}{\text{kW/m}}^{2}.[/latex] How long does it take for [latex]1.8×{10}^{9}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] to arrive on an area of [latex]1\text{.}00\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex]?
- Suppose you have a device that extracts energy from ocean breakers in direct proportion to their intensity. If the device produces 10.0 kW of power on a day when the breakers are 1.20 m high, how much will it produce when they are 0.600 m high?
- Engineering Application (a) A photovoltaic array of (solar cells) is 10.0% efficient in gathering solar energy and converting it to electricity. If the average intensity of sunlight on one day is [latex]700\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2},[/latex] what area should your array have to gather energy at the rate of 100 W? (b) What is the maximum cost of the array if it must pay for itself in two years of operation averaging 10.0 hours per day? Assume that it earns money at the rate of 9.00 ¢ per kilowatt-hour.
- A microphone receiving a pure sound tone feeds an oscilloscope, producing a wave on its screen. If the sound intensity is originally [latex]\text{2.00}×{\text{10}}^{\text{–5}}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2},[/latex] but is turned up until the amplitude increases by 30.0%, what is the new intensity?
- Medical Application (a) What is the intensity in [latex]{\text{W/m}}^{2}[/latex] of a laser beam used to burn away cancerous tissue that, when 90.0% absorbed, puts 500 J of energy into a circular spot 2.00 mm in diameter in 4.00 s? (b) Discuss how this intensity compares to the average intensity of sunlight (about [latex]700\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex]) and the implications that would have if the laser beam entered your eye. Note how your answer depends on the time duration of the exposure.
Glossary
- intensity
- power per unit area
power per unit area

