"

Oscillatory Motion and Waves and Physics of Hearing.

123 Forced Oscillations and Resonance

Learning Objectives

  • Observe resonance of a paddle ball on a string.
  • Observe amplitude behavior in a damped harmonic oscillator.
The figure shows the panel of the piano containing the strings, which are visibly in horizontal lines. Just below the strings is the wooden block of the piano containing the different type string handle bars and blocks.
Figure 123.1: You can cause the strings in a piano to vibrate simply by producing sound waves from your voice. (credit: Matt Billings, Flickr)

When you sit in front of a piano and sing a loud, brief note while the dampers are off, the piano may “sing back” that same note. This occurs because the strings that share the same natural frequency as your voice begin to vibrate. This is a compelling example of resonance—a phenomenon that arises when an object is driven at its natural frequency, causing its amplitude to increase significantly.

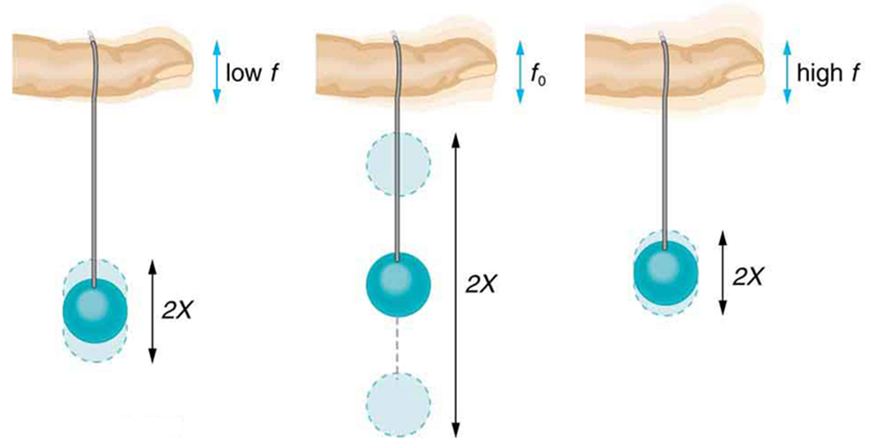
Now consider a toy like the paddle ball, shown in Figure 123.2. If you gently bounce the ball by moving your finger slowly, the ball follows with minimal motion. However, if you increase the driving frequency and approach the system’s natural frequency, the amplitude of oscillation increases substantially. When the frequency of the input matches the natural frequency, the system enters resonance and the oscillations grow with each cycle.

The given figure shows three pictures of a horizontal viewed single finger containing a string, suspended downward vertically, being tied to a paddle ball at its downward end. In the first figure the ball is stretching up and down very slowly having less displacement, the displacement shown in the figures as faded shades of the ball and is depicted as 2X. Whereas in the second figure the movement of the ball is highest, while in the third the movement is least. In all the three figures the ball is at its equilibrium with respect to its movement. The frequency, f, for the first figure is very low, for the second figure as f not, while for the third figure it is highest.
Figure 123.2: The paddle ball on a rubber string exhibits resonance when driven at its natural frequency [latex]{f}_{0}[/latex], resulting in large-amplitude oscillations. Off-resonance driving produces smaller responses.

The graph in Figure 123.3 shows how the amplitude of a damped oscillator varies with the frequency of a periodic driving force. All curves peak at the resonant frequency. Systems with less damping exhibit a sharper and higher peak—meaning greater energy is efficiently transferred into oscillation.

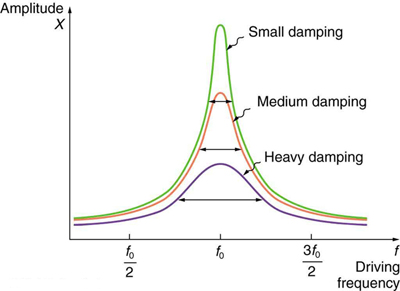
The given graph is of amplitude, X, along y axis versus driving frequency f, along x axis. There are three points on the x axis as f not divided by two, f not, three multiply f not divided by two. There are three curves along the x axis, in a one crest oscillation way, which are one over each other in correspondence. The curves start at a point just over the origin point and ends up at a same level along the x axis on the far right. The crests of the three curves are exactly over the f not point. The uppermost crest shows the small damping, whereas the middle one shows the medium damping, and the last one below shows the heavy damping.
Figure 123.3: Amplitude of a harmonic oscillator as a function of the driving frequency. Lower damping results in a higher, narrower resonance peak. Greater damping produces a broader, lower peak.

In practical terms, minimal damping yields sharp resonance useful in systems like musical instruments, where precise tuning is essential. Heavily damped systems, like a car’s suspension, suppress large oscillations and respond more broadly across driving frequencies.

This principle has wide applications. Radios resonate at the frequency of a selected station. MRI machines resonate with atomic nuclei to create diagnostic images. Even biological systems like the chest cavity operate at resonant frequencies—your diaphragm and chest wall act as a driven oscillator tuned for efficient airflow during breathing.

But resonance isn’t always desirable. In Figure 123.4, the Tacoma Narrows Bridge collapsed due to wind-induced resonance. Similarly, the Millennium Bridge in London briefly closed to resolve pedestrian-induced oscillations. These cases highlight the potential dangers when systems resonate without proper damping.

The figure shows a black and white photo of the Tacoma Narrows Bridge, from the left side view. The middle of the bridge is shown here in an oscillating state due to heavy cross winds.
Figure 123.4: In 1940, the Tacoma Narrows Bridge collapsed due to resonance caused by wind. Reduced damping allowed oscillations to grow uncontrollably. (credit: PRI’s Studio 360, via Flickr)

Check Your Understanding

Question: A famous magic trick involves a performer singing a note that causes a crystal glass to shatter. How does this work?

Answer: The trick works by matching the note to the natural frequency of the glass. The sound wave causes the glass to resonate, increasing oscillation amplitude until the structural integrity fails and it shatters.

Section Summary

  • A system’s natural frequency is the frequency at which it oscillates when free of external driving or damping forces.
  • A periodic driving force tuned to the system’s natural frequency produces resonance, leading to large-amplitude oscillations.
  • Lower damping results in sharper and higher resonance peaks; higher damping reduces peak amplitude but increases the range of effective driving frequencies.

Conceptual Questions

  1. Why are soldiers in general ordered to “route step” (walk out of step) across a bridge?

Problems & Exercises

  1. How much energy must the shock absorbers of a 1200-kg car dissipate in order to damp a bounce that initially has a velocity of 0.800 m/s at the equilibrium position? Assume the car returns to its original vertical position.
  2. If a car has a suspension system with a force constant of [latex]5\text{.}\text{00}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N/m}[/latex], how much energy must the car’s shocks remove to dampen an oscillation starting with a maximum displacement of 0.0750 m?
  3. (a) How much will a spring that has a force constant of 40.0 N/m be stretched by an object with a mass of 0.500 kg when hung motionless from the spring? (b) Calculate the decrease in gravitational potential energy of the 0.500-kg object when it descends this distance. (c) Part of this gravitational energy goes into the spring. Calculate the energy stored in the spring by this stretch, and compare it with the gravitational potential energy. Explain where the rest of the energy might go.
  4. Suppose you have a 0.750-kg object on a horizontal surface connected to a spring that has a force constant of 150 N/m. There is simple friction between the object and surface with a static coefficient of friction [latex]{\mu }_{\text{s}}=0\text{.}\text{100}[/latex]. (a) How far can the spring be stretched without moving the mass? (b) If the object is set into oscillation with an amplitude twice the distance found in part (a), and the kinetic coefficient of friction is [latex]{\mu }_{\text{k}}=0\text{.}\text{0850}[/latex], what total distance does it travel before stopping? Assume it starts at the maximum amplitude.
  5. Engineering Application: A suspension bridge oscillates with an effective force constant of [latex]1\text{.}\text{00}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{N/m}[/latex]. (a) How much energy is needed to make it oscillate with an amplitude of 0.100 m? (b) If soldiers march across the bridge with a cadence equal to the bridge’s natural frequency and impart [latex]1\text{.}\text{00}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex] of energy each second, how long does it take for the bridge’s oscillations to go from 0.100 m to 0.500 m amplitude?

Glossary

natural frequency
the frequency at which a system would oscillate if there were no driving and no damping forces
resonance
the phenomenon of driving a system with a frequency equal to the system’s natural frequency
resonate
a system being driven at its natural frequency
MRI
(Magnetic Resonance Imaging) – A noninvasive medical imaging technique that uses strong magnetic fields and radio waves to produce detailed images of the internal structures of the body. MRI is particularly effective for visualizing soft tissues, such as the brain, muscles, and organs, without using ionizing radiation.
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book