"

Oscillatory Motion and Waves and Physics of Hearing.

118 Simple Harmonic Motion: A Special Periodic Motion

Learning Objectives

  • Describe a simple harmonic oscillator.
  • Explain the link between simple harmonic motion and waves.

The oscillations of systems where the net force can be described by Hooke’s law are especially important because they are both common and simple. This type of motion is known as simple harmonic motion (SHM), and the system itself is called a simple harmonic oscillator.

If the system experiences no damping from friction or other non-conservative forces, it will oscillate symmetrically around an equilibrium position. Figure 118.1 shows an object attached to a spring on a frictionless surface, undergoing SHM with equal displacement on either side of equilibrium. The amplitude [latex]X[/latex] is the maximum displacement from equilibrium, and it reflects the energy of the oscillation. The units of amplitude and displacement depend on the system (e.g., meters for a spring, pressure units for sound waves).

Take-Home Experiment: SHM and the Marble

Place a marble in a bowl shaped like a hemisphere. Tilt the bowl periodically to roll the marble from one side to the other. Observe the regularity of motion. What is the restoring force in this setup? What role does your applied force play in maintaining SHM?

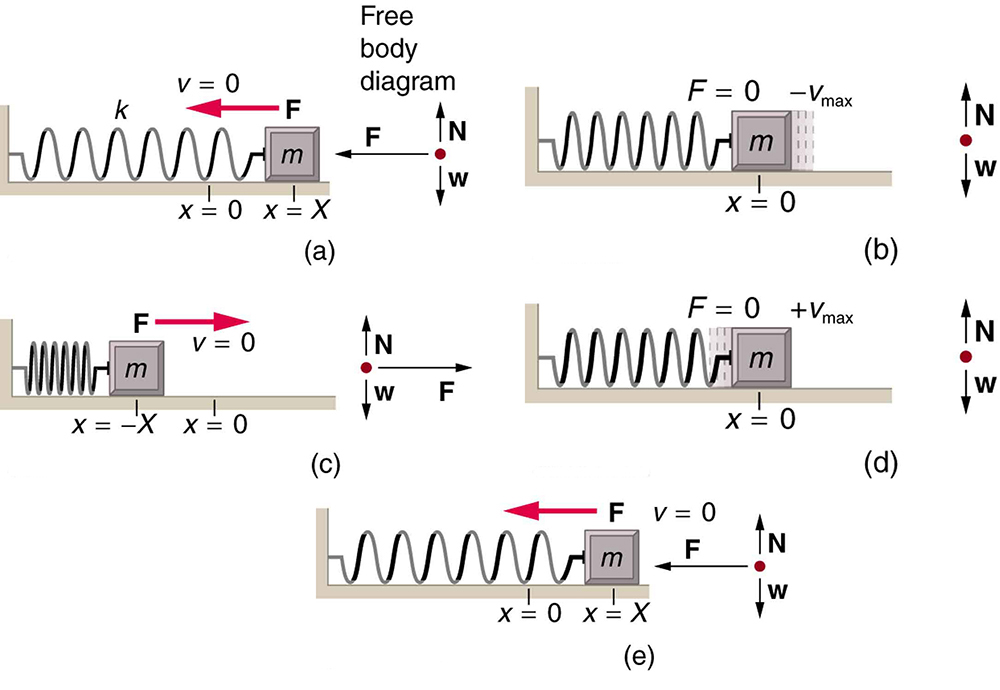
The figure a shows a spring on a frictionless surface attached to a bar or wall from the left side. On the right side of the spring, an object attached to it with mass m, its amplitude is given by X, and X is equal to zero at the equilibrium level. Force F is applied to it from the right side, shown with left direction pointed red arrow and velocity v is equal to zero. A direction point showing the north and west direction is also given alongside this figure as well as with other four figures. In figure b, after the force has been applied the object moves to the left compressing the spring a bit. And the displaced area of the object from its initial point is shown in sketched dots. The F here is equal to zero and the v is max in negative direction. In figure c, the spring has been compressed to the maximum level, and the amplitude is negative X. Now the direction of force changes to the rightward direction, shown with right direction pointed red arrow and the velocity v is zero. In figure d the spring is shown released from the compressed level and the object has moved toward the right side up to the equilibrium level. The F is zero, and the velocity v is maximum. In figure e the spring has been stretched loose to the maximum level and the object has moved to the far right. Now again the velocity here is equal to zero and the direction of force again is to the left hand side, shown here as F is equal to zero.
Figure 118.1: An object attached to a spring on a frictionless surface undergoes simple harmonic motion. When displaced, it oscillates with amplitude [latex]X[/latex] and period [latex]T[/latex]. Maximum speed occurs at equilibrium. A stiffer spring (larger [latex]k[/latex]) or smaller mass reduces the period.

What makes SHM so valuable? A key feature is that the period [latex]T[/latex] and frequency [latex]f[/latex] of SHM are independent of amplitude. For instance, a guitar string vibrates at the same frequency regardless of how hard it is plucked. This constancy makes SHM useful for timekeeping devices.

However, two physical quantities do influence the period: the system’s stiffness and its mass. A stiffer system (larger [latex]k[/latex]) has a shorter period. Conversely, a more massive system oscillates more slowly. Thus, both [latex]m[/latex] and [latex]k[/latex] directly affect SHM’s timing properties.

Period of a Simple Harmonic Oscillator

The period [latex]T[/latex] is calculated as:

[latex]T = 2\pi \sqrt{\frac{m}{k}}[/latex]

Since [latex]f = \frac{1}{T}[/latex], the frequency [latex]f[/latex] is:

[latex]f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}[/latex]

Neither equation depends on amplitude, highlighting one of SHM’s defining characteristics.

Take-Home Experiment: Mass and Ruler Oscillations

Secure two identical rulers to the edge of a table, leaving equal lengths extended. Attach a heavy object (like coins) to the end of one. Pluck both and observe how mass influences the period. Count how many cycles occur in a fixed time, and measure the period of each.

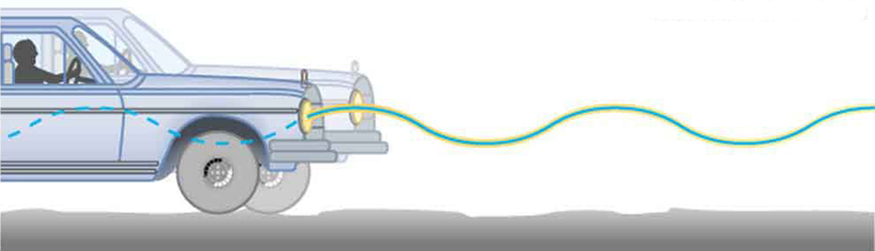
Example 118.1: Calculate the Frequency and Period of Oscillations: Bad Shock Absorbers in a Car

If the shock absorbers in a car go bad, then the car will oscillate at the least provocation, such as when going over bumps in the road and after stopping (See Figure 118.2). Calculate the frequency and period of these oscillations for such a car if the car’s mass (including its load) is 900 kg and the force constant ([latex]k[/latex]) of the suspension system is [latex]6\text{.}\text{53}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N/m}[/latex].

Strategy

The frequency of the car’s oscillations will be that of a simple harmonic oscillator as given in the equation [latex]f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}[/latex]. The mass and the force constant are both given.

Solution

  1. Enter the known values of k and m:
    [latex]f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}=\frac{1}{2\pi }\sqrt{\frac{6\text{.}\text{53}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N/m}}{\text{900}\phantom{\rule{0.25em}{0ex}}\text{kg}}}.[/latex]
  2. Calculate the frequency:
    [latex]\frac{1}{2\pi }\sqrt{\text{72.}6/{\text{s}}^{–2}}=1\text{.}{\text{3656}/\text{s}}^{\text{–1}}\approx 1\text{.}{\text{36}/\text{s}}^{\text{–1}}=\text{1.36 Hz}.[/latex]
  3. You could use [latex]T=2\pi \sqrt{\frac{m}{k}}[/latex] to calculate the period, but it is simpler to use the relationship [latex]T=1/f[/latex] and substitute the value just found for [latex]f[/latex]:
    [latex]T=\frac{1}{f}=\frac{1}{1\text{.}\text{356}\phantom{\rule{0.25em}{0ex}}\text{Hz}}=0\text{.}\text{738}\phantom{\rule{0.25em}{0ex}}\text{s}.[/latex]

Discussion

The values of [latex]T[/latex] and [latex]f[/latex] both seem about right for a bouncing car. You can observe these oscillations if you push down hard on the end of a car and let go.

The Link between Simple Harmonic Motion and Waves

If you were to take a time-exposure photograph of a bouncing car driving by, the headlight would leave behind a wavelike trail, as shown in Figure 118.2. Similarly, Figure 118.3 shows the trace left by an object bouncing on a spring recorded on a moving strip of paper. In both cases, the path is sinusoidal. This illustrates the deep connection between simple harmonic motion (SHM) and sine waves.

 

The figure shows the front right side of a running car on an uneven rough surface which also shows the driver in the driving seat. There is an oscillating sine wave drawn from left to the right side horizontally throughout the figure.
Figure 118.2: The bouncing car makes a wavelike motion. If the restoring force in the suspension system follows Hooke’s law, the wave is a sine function. (The trace is made by the car’s headlight.)
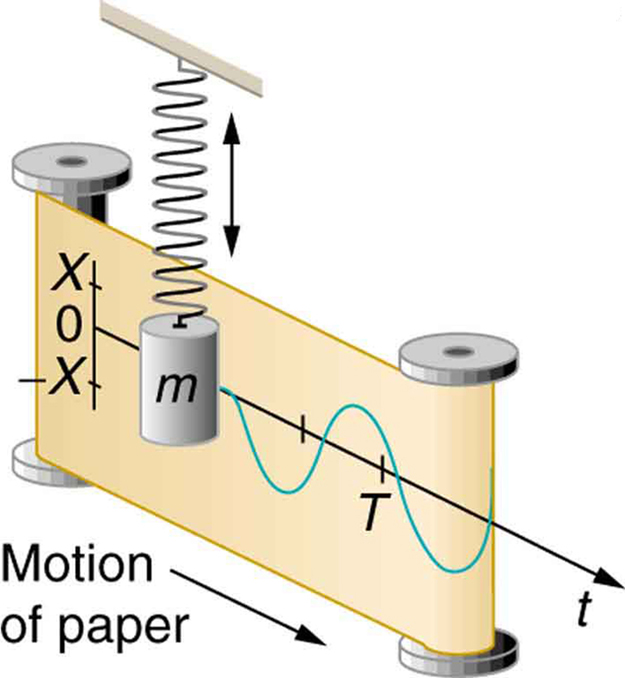
There are two iron paper roll bars standing vertically with a paper strip stitched from one bar to the other. There is a vertical hanging spring just over the middle of the two bars, perpendicular to the strip of the paper, having an object with mass m tied to it. There is a line graph with amplitude scale as X, zero and negative X on the left side of the paper strip, vertically over each other with their points marked. A perpendicular line is drawn through this amplitude scale toward the right with a point T marked over it, showing the time duration of the amplitude. This line has an oscillating wave drawn through it.
Figure 118.3: The vertical position of an object bouncing on a spring is recorded on a moving strip of paper, resulting in a sine wave trace.

The displacement [latex]x(t)[/latex] in any SHM system (with a restoring force obeying Hooke’s law) is described by:

[latex]x(t) = X \cos\left(\frac{2\pi t}{T}\right)[/latex]

Here, [latex]X[/latex] is the amplitude of motion, and [latex]T[/latex] is the period. At [latex]t = 0[/latex], the object is at maximum displacement, [latex]x(0) = X[/latex]. Because cosine is periodic, the object returns to the same position after one period.

The corresponding velocity [latex]v(t)[/latex] is obtained by differentiating the displacement function:

[latex]v(t) = -v_{\text{max}} \sin\left(\frac{2\pi t}{T}\right)[/latex]

where the maximum velocity is:

[latex]v_{\text{max}} = \frac{2\pi X}{T} = X\sqrt{\frac{k}{m}}[/latex]

The negative sign indicates that the velocity is directed opposite the displacement when the motion begins (i.e., the object starts moving toward equilibrium).

Acceleration [latex]a(t)[/latex] follows from Newton’s second law:

[latex]a(t) = -\frac{kX}{m} \cos\left(\frac{2\pi t}{T}\right)[/latex]

Notice that acceleration is proportional to and in the opposite direction of displacement: a hallmark of SHM.

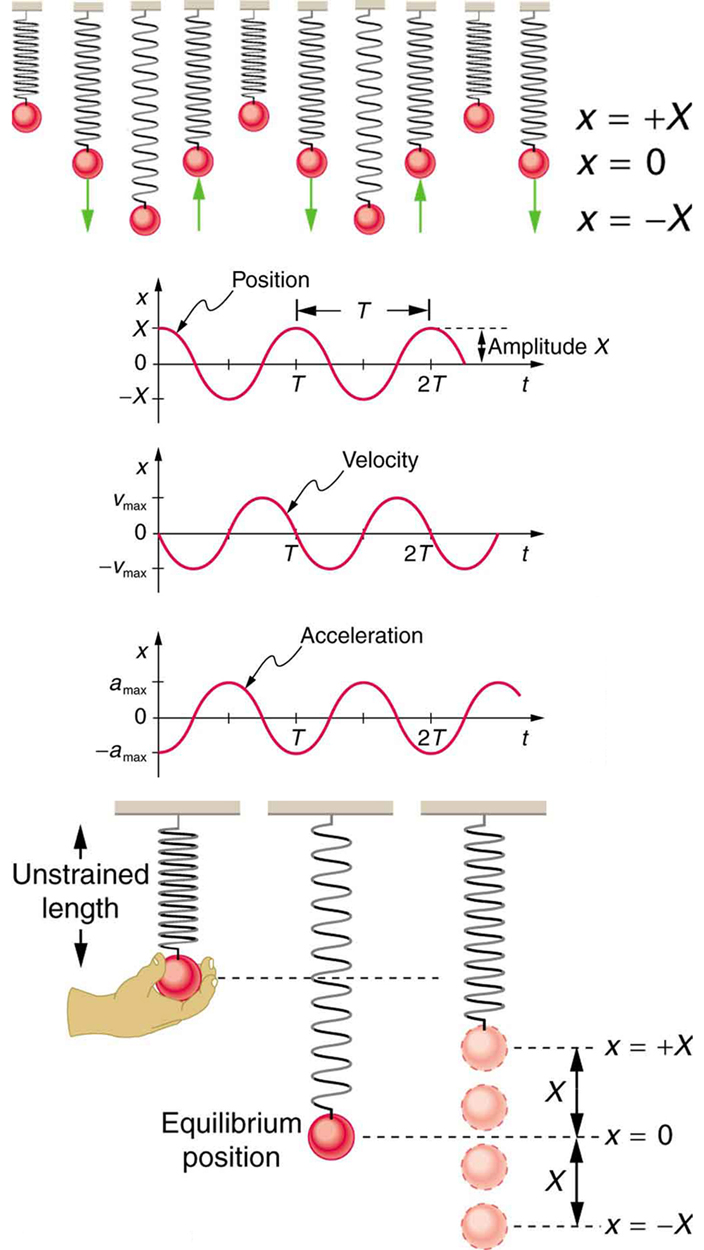
In the figure at the top there are ten springboards with objects of different mass values tied to them. This makes some springs highly compressed some as loosely stretched and some at equilibrium, which are shown as red spherical shaped. Alongside the figure there is a scale given for different amplitude values as x equal to positive X, zero and negative X. the upward and downward pointing arrows are shown with a few springboards. In the second figure there are three graphs. The first graph shows distance covered in form of a sine wave starting from a point x units on positive y-axis. The height of the wave above x-axis is marked as amplitude. The gap between two consecutive crests is marked as T. Below first graph there is another graph showing velocity in form of a sine wave starting from the origin downward. In the third graph below the second one, acceleration is shown in the form of sine wave starting from x units on the negative y-axis upward. In the last figure three position of a spring are shown. The first position shows the unstretched length of a spring pendulum. A hand is holding the bob of the pendulum. In the second position the equilibrium position of the spring and bob is shown. This position is lower the first one. In the third case the up and down oscillations of the spring pendulum are shown. The bob is moving x units in upward and downward directions alternatively.
Figure 118.4: Graphs of [latex]x(t)[/latex], [latex]v(t)[/latex], and [latex]a(t)[/latex] for SHM. Initially, the object is at maximum displacement [latex]X[/latex] with zero velocity. As the object passes through equilibrium, speed is at its maximum. Acceleration and displacement always have opposite signs.

These mathematical expressions are fundamental to analyzing and visualizing wave-like motion in SHM. They also lay the groundwork for understanding wave interference and superposition.

Check Your Understanding

1. Suppose you pluck a banjo string. You hear a single note that gradually becomes quieter. What happens to the period, frequency, and amplitude as the sound fades?

Answer: Period and frequency remain constant. Only the amplitude decreases as the volume fades.

2. A babysitter pushes a child on a swing. At the point of maximum displacement [latex]x[/latex], where is the corresponding point on the wave?

Answer: The displacement [latex]x[/latex] corresponds to the amplitude of the wave — the peak (top or bottom) of the sine curve.

PhET Explorations: Masses and Springs

The Masses and Springs simulation by PhET offers an interactive virtual lab where students can explore the behavior of mass-spring systems under different conditions. In this simulation, you can:

  • Hang various masses from springs and observe how they stretch.
  • Adjust the spring stiffness (spring constant [latex]k[/latex]) and observe its effect on oscillation period and amplitude.
  • Add or remove damping to simulate frictional or resistive forces that gradually reduce motion over time.
  • Transport the experiment to different planets or environments (e.g., Moon, Jupiter) to examine how changes in gravitational acceleration affect motion.
  • Visualize the transformation between kinetic energy, elastic potential energy, and thermal energy as the system oscillates.
  • Slow down or speed up time to carefully observe energy changes and dynamics of motion.

A built-in energy chart displays real-time graphs showing how energy is conserved and converted between forms in the system. This reinforces key concepts such as the conservation of mechanical energy in ideal systems and the impact of non-conservative forces when damping is introduced.

 

Section Summary

  • Simple harmonic motion (SHM) is oscillatory motion for a system in which the net restoring force is described by Hooke’s law. A system that exhibits SHM is called a simple harmonic oscillator.
  • The maximum displacement from equilibrium is called the amplitude [latex]X[/latex]. The period [latex]T[/latex] and frequency [latex]f[/latex] of a simple harmonic oscillator are given by:
    [latex]T = 2\pi \sqrt{\frac{m}{k}}[/latex]
    [latex]f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}[/latex]

    where [latex]m[/latex] is the mass of the object and [latex]k[/latex] is the spring constant.

  • The displacement as a function of time is:
    [latex]x(t) = X \cos\left(\frac{2\pi t}{T}\right)[/latex]
  • The velocity as a function of time is:
    [latex]v(t) = -v_{\text{max}} \sin\left(\frac{2\pi t}{T}\right)[/latex]

    where the maximum velocity is:

    [latex]v_{\text{max}} = X \sqrt{\frac{k}{m}}[/latex]
  • The acceleration as a function of time is:
    [latex]a(t) = -\frac{kX}{m} \cos\left(\frac{2\pi t}{T}\right)[/latex]

Conceptual Questions

  1. What conditions must be met to produce simple harmonic motion?
    1. If frequency is not constant for some oscillation, can the oscillation be simple harmonic motion?
    2. Can you think of any examples of harmonic motion where the frequency may depend on the amplitude?
  2. Give an example of a simple harmonic oscillator, specifically noting how its frequency is independent of amplitude.
  3. Explain why you expect an object made of a stiff material to vibrate at a higher frequency than a similar object made of a spongy material.
  4. As you pass a freight truck with a trailer on a highway, you notice that its trailer is bouncing up and down slowly. Is it more likely that the trailer is heavily loaded or nearly empty? Explain your answer.
  5. Some people modify cars to be much closer to the ground than when manufactured. Should they install stiffer springs? Explain your answer.

Problems & Exercises

  1. A type of cuckoo clock keeps time by having a mass bouncing on a spring, usually something cute like a cherub in a chair. What force constant is needed to produce a period of 0.500 s for a 0.0150-kg mass?
  2. If the spring constant of a simple harmonic oscillator is doubled, by what factor will the mass of the system need to change in order for the frequency of the motion to remain the same?
  3. A 0.500-kg mass suspended from a spring oscillates with a period of 1.50 s. How much mass must be added to the object to change the period to 2.00 s?
  4. By how much leeway (both percentage and mass) would you have in the selection of the mass of the object in the previous problem if you did not wish the new period to be greater than 2.01 s or less than 1.99 s?
  5. Suppose you attach the object with mass [latex]m[/latex] to a vertical spring originally at rest, and let it bounce up and down. You release the object from rest at the spring’s original rest length. (a) Show that the spring exerts an upward force of [latex]2.00\phantom{\rule{0.25em}{0ex}}\mathrm{mg}[/latex] on the object at its lowest point. (b) If the spring has a force constant of [latex]\text{10}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{N/m}[/latex] and a 0.25-kg-mass object is set in motion as described, find the amplitude of the oscillations. (c) Find the maximum velocity.
  6. A diver on a diving board is undergoing simple harmonic motion. Her mass is 55.0 kg and the period of her motion is 0.800 s. The next diver is a male whose period of simple harmonic oscillation is 1.05 s. What is his mass if the mass of the board is negligible?
  7. Suppose a diving board with no one on it bounces up and down in a simple harmonic motion with a frequency of 4.00 Hz. The board has an effective mass of 10.0 kg. What is the frequency of the simple harmonic motion of a 75.0-kg diver on the board?
    The figure shows a little kid, about ten to twelve months old, standing in a toy jolly jumper, which is tied to the ceiling hook by its four spring belts.
    Figure 118.6: This child’s toy relies on springs to keep infants entertained. (credit: By Humboldthead, Flickr)
  8. The device pictured in Figure 118.6 entertains infants while keeping them from wandering. The child bounces in a harness suspended from a door frame by a spring constant. (a) If the spring stretches 0.250 m while supporting an 8.0-kg child, what is its spring constant? (b) What is the time for one complete bounce of this child? (c) What is the child’s maximum velocity if the amplitude of her bounce is 0.200 m?
  9. A 90.0-kg skydiver hanging from a parachute bounces up and down with a period of 1.50 s. What is the new period of oscillation when a second skydiver, whose mass is 60.0 kg, hangs from the legs of the first, as seen in Figure 118.7.
The figure shows two skydivers midway through the air, with both with open having their parachutes open.
Figure 118.7: The oscillations of one skydiver are about to be affected by a second skydiver. (credit: U.S. Army, www.army.mil)

Glossary

amplitude
the maximum displacement from the equilibrium position of an object oscillating around the equilibrium position
simple harmonic motion
the oscillatory motion in a system where the net force can be described by Hooke’s law
simple harmonic oscillator
a device that implements Hooke’s law, such as a mass that is attached to a spring, with the other end of the spring being connected to a rigid support such as a wall
wave interference
the phenomenon that occurs when two or more waves meet at the same point in space, combining to form a new wave pattern. Interference can be constructive (waves reinforce each other, increasing amplitude) or destructive (waves partially or completely cancel each other, reducing amplitude)
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book