"

Oscillatory Motion and Waves and Physics of Hearing.

116 Hooke’s Law: Stress and Strain Revisited

Learning Objectives

  • Explain Newton’s third law of motion in the context of stress and deformation.
  • Describe how restoring force relates to displacement in oscillating systems.
  • Calculate the energy stored in systems obeying Hooke’s law, such as stretched strings or biological tissues.
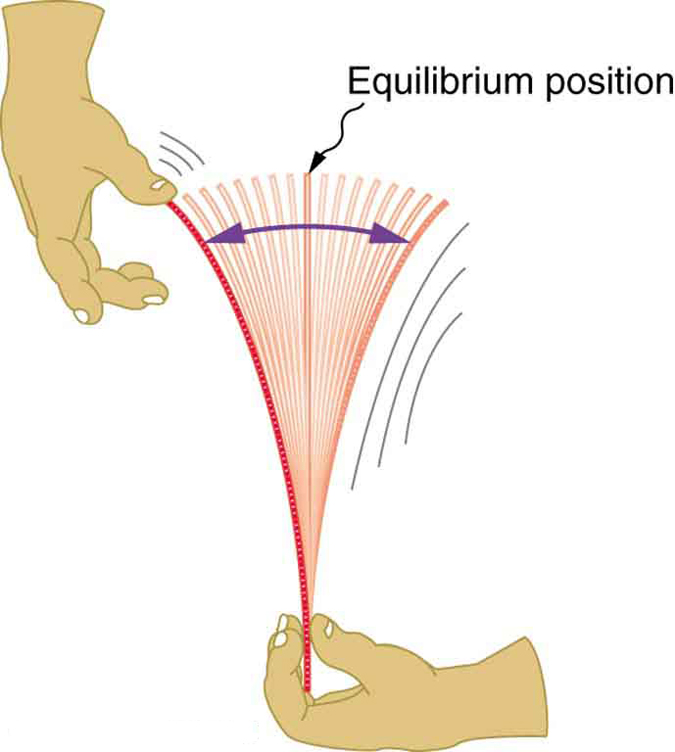
In this figure a hand holding a ruler tightly at the bottom is shown. The other hand pulls the top of the ruler and then releases it. Then the ruler starts vibrating, and oscillates around the equilibrium position. A vertical line is shown to mark the equilibrium position. A curved double-headed arrow shows the span of the oscillation.
Figure 116.1: When displaced from its vertical equilibrium position, this plastic ruler oscillates back and forth due to a restoring force that opposes the displacement. When the ruler bends left, a restoring force acts to the right, and vice versa.

According to Newton’s first law, an object that is oscillating must be under the influence of forces—otherwise, it would move in a straight line at constant speed. For instance, when a plastic ruler is pulled to one side and released (Figure 116.1), it deforms and experiences a restoring force that opposes the deformation. Once released, this force pulls the ruler back toward its original position. However, the ruler gains momentum and overshoots, bending in the opposite direction. The cycle repeats, forming an oscillatory motion that eventually dies out due to energy dissipation from internal friction or air resistance.

The simplest type of oscillatory motion occurs when the restoring force is directly proportional to the displacement from equilibrium. This relationship, known as Hooke’s law, is described by the equation:

[latex]F = -kx[/latex]

Here, [latex]F[/latex] is the restoring force, [latex]x[/latex] is the displacement from equilibrium, and [latex]k[/latex] is the force constant, which characterizes the stiffness of the system. The negative sign indicates that the force acts in the opposite direction of the displacement.

A series of illustrations of vibrating plastic rulers is shown demonstrating Hooke’s law.
Figure 116.2: (a) The ruler is released and the restoring force pulls it toward equilibrium. (b) At equilibrium, the net force is zero, but the ruler’s momentum carries it forward. (c) The force now acts in the opposite direction, slowing the ruler and pushing it back. (d) Momentum takes it past equilibrium again. (e) In the absence of friction, the cycle would continue indefinitely.

The value of the force constant [latex]k[/latex] indicates how stiff or rigid the system is. A larger [latex]k[/latex] means the system resists deformation more strongly. The units of [latex]k[/latex] are newtons per meter (N/m). For example, in biological tissues or tendons, higher stiffness implies larger values of [latex]k[/latex], affecting how they store and release elastic energy.

Figure 116.3 shows a graph of the restoring force versus displacement for a system obeying Hooke’s law—such as a spring. The linearity of the graph confirms the proportional relationship, and the slope gives the value of [latex]k[/latex]. This principle is often explored in laboratory settings to test biological or mechanical materials.

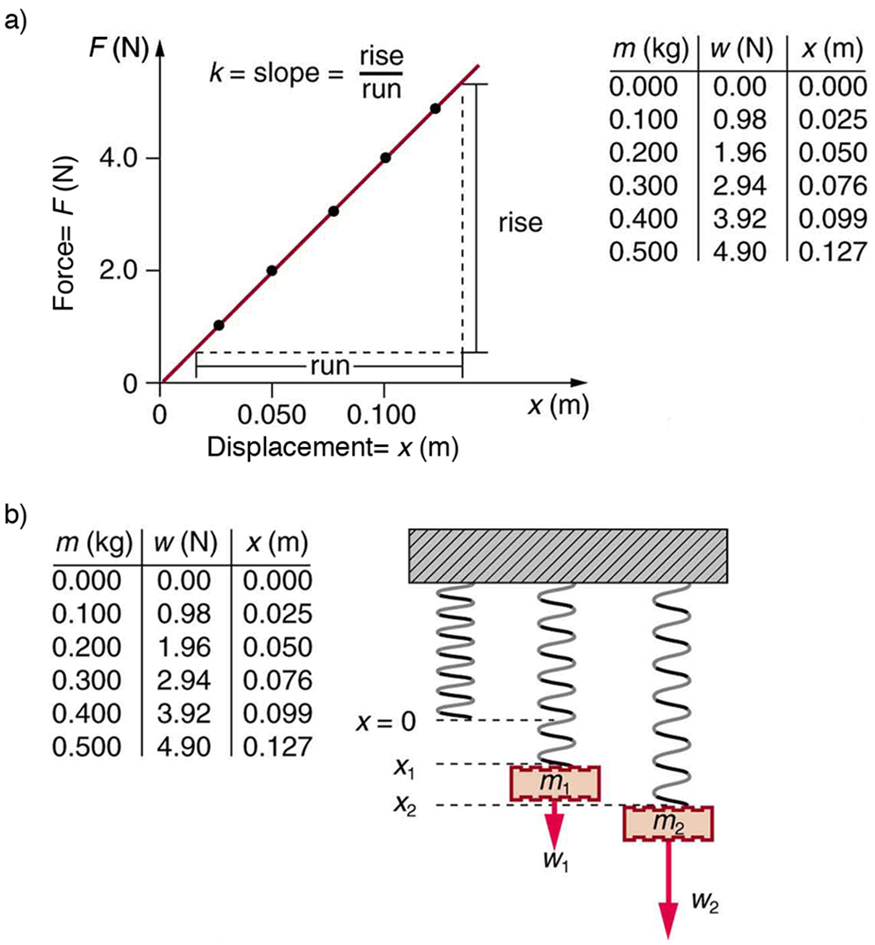
The given figure a is the graph of restoring force versus displacement. The displacement is given by x in meters along x axis, with scales from zero to point zero five zero, then to point one zero, then forward. The restoring force is given by F in unit newton along y axis, with scales from zero to two point zero to four point zero to forward. The graph line starts from zero and goes to upward to point where x is greater than point one zero and F is greater than four point zero with intersection dots at equal distances on the slope line. The slope is depicted by K which is given by rise along y-axis upon run along x axis . The values of mass in kilogram, weight in newtons, and displacement in meters are given along with the graph in a tabular format. In the figure b a horizontal weight bar is shown with three weight measuring springs tied to its lower part, hanging in the downward vertical direction. The first bar has no mass hanging through it, showing zero displacement, as x is equal to zero. It is the least stretched spring downward. The second spring has mass m one tied to it which exerts a force w one, on the spring, which causes displacement in the spring shown here to be x one. Similarly, the third spring is most stretched downward with a mass m two hanging through it with force w two and displacement x two. The values of mass in kg, weight in newtons and displacement in meters are given with the graph in a tabular format.
Figure 116.3: (a) A plot of restoring force versus displacement reveals a straight-line relationship consistent with Hooke’s law. The slope of the graph represents the force constant [latex]k[/latex]. (b) Experimental data were obtained by measuring how different weights stretch a spring. The restoring force equals the weight when the mass is in equilibrium.

Example 116.1: How Stiff Are Car Springs?

The figure shows the left side of a hatchback car’s back area, showing the font of its rear wheel. There is an arrow on road pointing its head toward this wheel.
Figure 116.4: The mass of a car increases due to the introduction of a passenger. This affects the displacement of the car on its suspension system. (credit: exfordy on Flickr)

What is the force constant for the suspension system of a car that settles 1.20 cm when an 80.0-kg person gets in?

Strategy

Consider the car to be in its equilibrium position [latex]x=0[/latex] before the person gets in. The car then settles down 1.20 cm, which means it is displaced to a position [latex]x=-1\text{.}\text{20}×{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. At that point, the springs supply a restoring force [latex]F[/latex] equal to the person’s weight [latex]w=\text{mg}=\left(\text{80}\text{.}0\phantom{\rule{0ex}{0ex}}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)\left(9\text{.}\text{80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)=\text{784}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex]. We take this force to be [latex]F[/latex] in Hooke’s law. Knowing [latex]F[/latex] and [latex]x[/latex], we can then solve the force constant [latex]k[/latex].

Solution

  1. Solve Hooke’s law, [latex]F=-\text{kx}[/latex], for [latex]k[/latex]:
    [latex]k=-\frac{F}{x}.[/latex]

  2. Substitute known values and solve [latex]k[/latex]:

    [latex]\begin{array}{lll}k& =& -\frac{\text{784}\phantom{\rule{0.25em}{0ex}}\text{N}}{-1\text{.}\text{20}×{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}\text{m}}\\ & =& 6\text{.}\text{53}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N/m}.\end{array}[/latex]

Discussion

Note that [latex]F[/latex] and [latex]x[/latex] have opposite signs because they are in opposite directions—the restoring force is up, and the displacement is down. Also, note that the car would oscillate up and down when the person got in if it were not for damping (due to frictional forces) provided by shock absorbers. Bouncing cars are a sure sign of bad shock absorbers.

Energy in Hooke’s Law of Deformation

Whenever a system is deformed—such as when you pluck a guitar string or compress a spring—work must be done. That is, a force must act over a distance to cause the deformation. If none of the energy is lost to sound, heat, or motion, then all of the work is stored in the system as potential energy. For systems that obey Hooke’s law, this stored energy is known as elastic potential energy.

The elastic potential energy stored in a deformed system is given by the expression:

[latex]{\text{PE}}_{\text{el}} = \frac{1}{2}kx^2[/latex]

Here, [latex]{\text{PE}}_{\text{el}}[/latex] is the stored energy, [latex]k[/latex] is the force constant characterizing the stiffness of the system, and [latex]x[/latex] is the displacement from the system’s equilibrium position. This equation applies to any system—biological or mechanical—that exhibits linear elastic behavior.

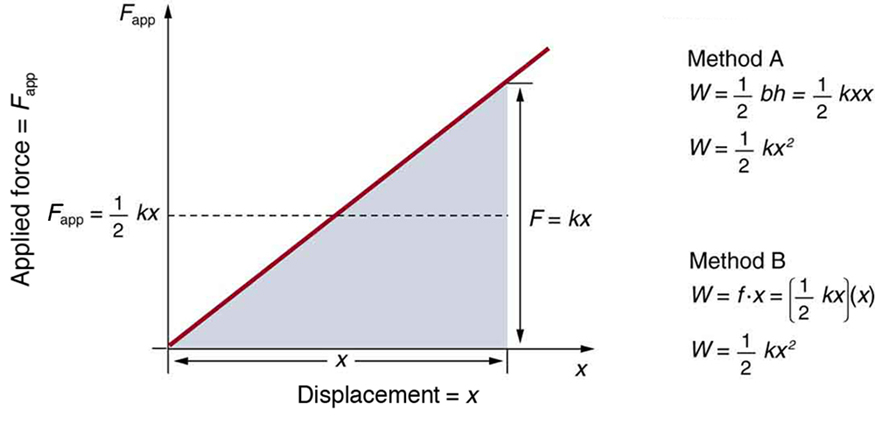
The energy stored in the system comes from the work done to deform it. That work is performed by an applied force [latex]F_{\text{app}}[/latex], which acts in the direction of displacement and opposes the restoring force. For systems following Hooke’s law, the applied force increases linearly with displacement:

[latex]F_{\text{app}} = kx[/latex]

Figure 116.5 shows a graph of [latex]F_{\text{app}}[/latex] versus [latex]x[/latex]. The work done on the system is the area under the curve. Because the force increases linearly from 0 to [latex]kx[/latex], this area forms a triangle. The work (and therefore the stored energy) can be calculated in two equivalent ways:

  • Method A: The area of the triangle is [latex]\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2}kx^2[/latex].
  • Method B: The average force is [latex]\frac{1}{2}kx[/latex], and the displacement is [latex]x[/latex], so the work is [latex]W = F_{\text{avg}} \cdot x = \left( \frac{1}{2}kx \right) \cdot x = \frac{1}{2}kx^2[/latex].
The graph here represents applied force, given along y-axis, versus deformation or displacement, given along x axis. The slope is linear slanting and the slope area is covered between x axis and the slope, given by F is equal to k multiplied by x, where k is constant and x is displacement. The force applied along y-axis is given by half of k multiplied by x. Along with the graph, two methods are provided to calculate weight, W. The first method gives the solution by multiplying half of b multiplied by h, whereas in the second we can get the solution by multiplying f with x.
Figure 116.5: A graph of applied force versus displacement for a system obeying Hooke’s law. The area under the line represents the work done to deform the system, which equals the [pb_glossary id="6001"]elastic potential energy[/pb_glossary] stored. Since the graph forms a triangle, the area (and energy stored) is given by [latex]W = \frac{1}{2}kx^2[/latex].

Example 116.2: Calculating Stored Energy: A Tranquilizer Gun Spring

We can use a toy gun’s spring mechanism to ask and answer two simple questions: (a) How much energy is stored in the spring of a tranquilizer gun that has a force constant of 50.0 N/m and is compressed 0.150 m? (b) If you neglect friction and the mass of the spring, at what speed will a 2.00-g projectile be ejected from the gun?

 

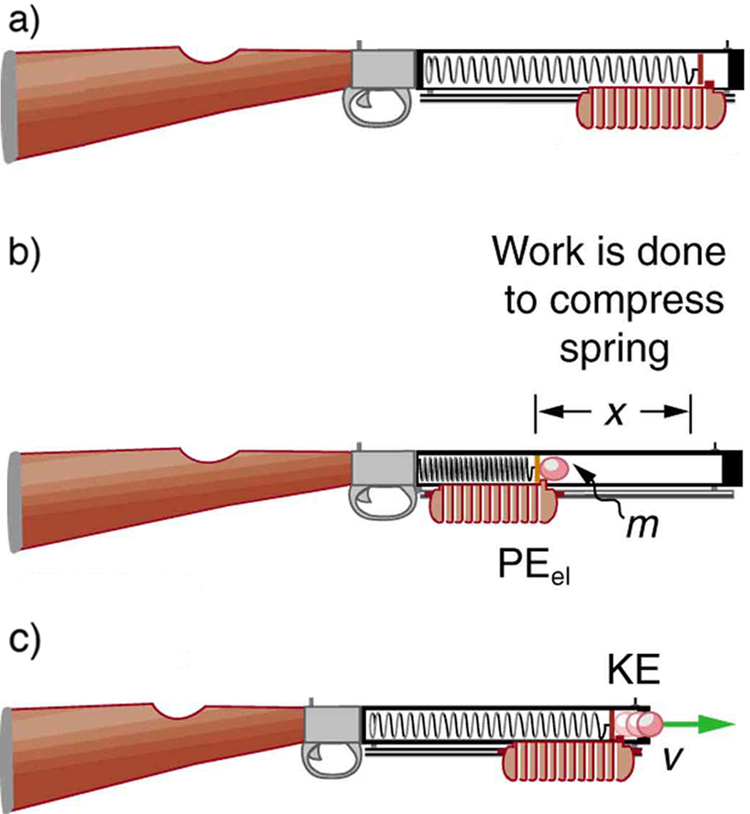
The figure a shows an artistic impression of a tranquilizer gun, which shows the inside of it revealing the gun spring and a panel just below it, in the outside area, attached to the spring. This stage shows the gun before it is cocked, and the spring is uncompressed covering the entire inside area. The figure b shows the gun with the spring in the compressed mode. The spring has been compressed to a distance x, where x distance shows the vacant area inside the gun through which the spring has been compressed. The panel is also moving along the spring. And a bullet of mass m is shown at the front of the compressed spring. The spring here has elastic potential energy, represented by P E sub e l. The figure c is the third stage of the above two stages of the gun. The spring here is released from the compressed stage releasing the bullet in the outer forward direction with velocity V and the spring’s potential energy is converted into kinetic energy, represented here by K E.
Figure 116.6: (a) In this image of the gun, the spring is uncompressed before being cocked. (b) The spring has been compressed a distance [latex]x[/latex], and the projectile is in place. (c) When released, the spring converts elastic potential energy [latex]{\text{PE}}_{\text{el}}[/latex] into kinetic energy.

Strategy for a

(a): The energy stored in the spring can be found directly from elastic potential energy equation, because [latex]k[/latex] and [latex]x[/latex] are given.

Solution for a

Entering the given values for [latex]k[/latex] and [latex]x[/latex] yields

[latex]\begin{array}{lll}{\text{PE}}_{\text{el}}& =& \frac{1}{2}{\mathrm{kx}}^{2}=\frac{1}{2}\left(\text{50}\text{.}0\phantom{\rule{0.25em}{0ex}}\text{N/m}\right){\left(0\text{.}\text{150}\phantom{\rule{0.25em}{0ex}}\text{m}\right)}^{2}=0\text{.}\text{563}\phantom{\rule{0.25em}{0ex}}\text{N}\cdot \text{m}\\ & =& 0\text{.}\text{563}\phantom{\rule{0.25em}{0ex}}\text{J}\end{array}[/latex]

Strategy for b

Because there is no friction, the potential energy is converted entirely into kinetic energy. The expression for kinetic energy can be solved for the projectile’s speed.

Solution for b

  1. Identify known quantities:
    [latex]{\text{KE}}_{\text{f}}={\text{PE}}_{\text{el}}\phantom{\rule{0.25em}{0ex}}or\phantom{\rule{0.25em}{0ex}}1/2{\mathit{mv}}^{2}=\left(1/2\right){\mathit{kx}}^{2}={\text{PE}}_{\mathrm{el}}=0\text{.}\text{563}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex]
  2. Solve for [latex]v[/latex]:
    [latex]v={\left[\frac{2{\text{PE}}_{\text{el}}}{m}\right]}^{1/2}={\left[\frac{2\left(0\text{.}\text{563}\phantom{\rule{0.25em}{0ex}}\text{J}\right)}{0\text{.}\text{002}\phantom{\rule{0.25em}{0ex}}\text{kg}}\right]}^{1/2}=\text{23}\text{.}7{\left(\text{J/kg}\right)}^{1/2}[/latex]
  3. Convert units: [latex]23.7\phantom{\rule{0.25em}{0ex}}\text{m}/\text{s}[/latex]

Discussion

(a) and (b): This projectile speed is impressive for a tranquilizer gun (more than 80 km/h). The numbers in this problem seem reasonable. The force needed to compress the spring is small enough for an adult to manage, and the energy imparted to the dart is small enough to limit the damage it might do. Yet, the speed of the dart is great enough for it to travel an acceptable distance.

Check Your Understanding

Concept Check

Question: Imagine holding a plastic ruler at one end and bending it with your other hand. When you let go, the ruler oscillates. How could you modify this experiment to increase the rigidity of the system?

Answer: Hold the ruler at its midpoint instead of one end. This effectively shortens the portion that oscillates, increasing the rigidity and resulting in faster oscillations.

Concept Check

Question: If you apply a deforming force to an object and allow it to reach equilibrium, what happens to the work you did on the object?

Answer: The work is stored in the object as elastic potential energy.

Section Summary

  • An oscillation is a repetitive back-and-forth motion of an object about an equilibrium position.
  • Oscillations can give rise to waves, which are disturbances that carry energy through space or matter.
  • The simplest types of oscillatory motion can be modeled using Hooke’s law:
    [latex]F = -kx[/latex]

    where [latex]F[/latex] is the restoring force, [latex]x[/latex] is the displacement from equilibrium, and [latex]k[/latex] is the force constant.

  • The elastic potential energy stored in a deformed system is:
    [latex]{\text{PE}}_{\text{el}} = \frac{1}{2}kx^2[/latex]

Conceptual Questions

  1. Describe a system in which elastic potential energy is stored.

Problems & Exercises

  1. Fish are hung on a spring scale to determine their mass (most fishermen feel no obligation to truthfully report the mass). (a) What is the force constant of the spring in such a scale if it the spring stretches 8.00 cm for a 10.0 kg load? (b) What is the mass of a fish that stretches the spring 5.50 cm? (c) How far apart are the half-kilogram marks on the scale?
  2. It is weigh-in time for the local under-85-kg rugby team. The bathroom scale used to assess eligibility can be described by Hooke’s law and is depressed 0.75 cm by its maximum load of 120 kg. (a) What is the spring’s effective spring constant? (b) A player stands on the scales and depresses it by 0.48 cm. Is he eligible to play on this under-85 kg team?
  3. One type of BB gun uses a spring-driven plunger to blow the BB from its barrel. (a) Calculate the force constant of its plunger’s spring if you must compress it 0.150 m to drive the 0.0500-kg plunger to a top speed of 20.0 m/s. (b) What force must be exerted to compress the spring?
  4. (a) The springs of a pickup truck act like a single spring with a force constant of [latex]1\text{.}\text{30}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{N/m}[/latex]. By how much will the truck be depressed by its maximum load of 1000 kg? (b) If the pickup truck has four identical springs, what is the force constant of each?
  5. When an 80.0-kg man stands on a pogo stick, the spring is compressed 0.120 m. (a) What is the force constant of the spring? (b) Will the spring be compressed more when he hops down the road?
  6. A spring has a length of 0.200 m when a 0.300-kg mass hangs from it, and a length of 0.750 m when a 1.95-kg mass hangs from it. (a) What is the force constant of the spring? (b) What is the unloaded length of the spring?

Glossary

deformation
displacement from equilibrium
elastic potential energy
potential energy stored as a result of deformation of an elastic object, such as the stretching of a spring
force constant
a constant related to the rigidity of a system: the larger the force constant, the more rigid the system; the force constant is represented by k
restoring force
force acting in opposition to the force caused by a deformation
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book