Thermodynamics
114 Statistical Interpretation of Entropy and the Second Law of Thermodynamics: The Underlying Explanation
Learning Objectives
- Identify probabilities in entropy.
- Analyze statistical probabilities in entropic systems.
Understanding Entropy through Probability

The second law of thermodynamics describes what happens in natural processes: heat flows from hot to cold, energy becomes less available to do work, and systems tend to become more disordered. But why does this happen? The answer lies in probability: disordered states are vastly more likely than ordered ones.
For example, when raindrops fall, they do so randomly in time and space. It is not impossible for rain to fall in a grid pattern, but it is extremely unlikely because disordered patterns are far more probable. This principle is the key to understanding entropy.
Coin Tosses and Probability
Consider tossing five fair coins. Each coin can land heads or tails. We’re interested in the number of heads, not the sequence. These are the possible macrostates:
Each macrostate corresponds to a certain number of microstates—specific outcomes like HHTHT or TTHHT. Some macrostates, like 3 heads and 2 tails, are more probable than others because they have more microstates associated with them.
Coin toss
Individual microstates
Number of microstates
5 heads, 0 tails
HHHHH
1
4 heads, 1 tail
HHHHT, HHHTH, HHTHH, HTHHH, THHHH
5
3 heads, 2 tails
HTHTH, THTHH, HTHHT, THHTH, THHHT HTHTH, THTHH, HTHHT, THHTH, THHHT
10
2 heads, 3 tails
TTTHH, TTHHT, THHTT, HHTTT, TTHTH, THTHT, HTHTT, THTTH, HTTHT, HTTTH
10
1 head, 4 tails
TTTTH, TTTHT, TTHTT, THTTT, HTTTT
5
0 heads, 5 tails
TTTTT
1
Total: 32
The system is more likely to transition from ordered states (like 5 heads) to disordered states (like 3 heads and 2 tails), simply because there are more microstates for disordered outcomes.
Scaling Up: The 100-Coin Toss
Now imagine tossing 100 coins. The number of possible microstates grows exponentially. The most ordered state (100 heads) has only 1 microstate. The most disordered state (50 heads, 50 tails) has an enormous number of microstates.
Macrostate
Number of microstates
Heads
Tails
(W)
100
0
1
99
1
[latex]1\text{.}0×{\text{10}}^{2}[/latex]
95
5
[latex]7\text{.}5×{\text{10}}^{7}[/latex]
90
10
[latex]1\text{.}7×{\text{10}}^{\text{13}}[/latex]
75
25
[latex]2\text{.}4×{\text{10}}^{\text{23}}[/latex]
60
40
[latex]1\text{.}4×{\text{10}}^{\text{28}}[/latex]
55
45
[latex]6\text{.}1×{\text{10}}^{\text{28}}[/latex]
51
49
[latex]9\text{.}9×{\text{10}}^{\text{28}}[/latex]
50
50
[latex]1\text{.}0×{\text{10}}^{\text{29}}[/latex]
49
51
[latex]9\text{.}9×{\text{10}}^{\text{28}}[/latex]
45
55
[latex]6\text{.}1×{\text{10}}^{\text{28}}[/latex]
40
60
[latex]1\text{.}4×{\text{10}}^{\text{28}}[/latex]
25
75
[latex]2\text{.}4×{\text{10}}^{\text{23}}[/latex]
10
90
[latex]1\text{.}7×{\text{10}}^{\text{13}}[/latex]
5
95
[latex]7\text{.}5×{\text{10}}^{7}[/latex]
1
99
[latex]1\text{.}0×{\text{10}}^{2}[/latex]
0
100
1
Total: [latex]1\text{.}\text{27}×{\text{10}}^{\text{30}}[/latex]
You’re more likely to get 50 heads than 100 heads by an astronomically large margin. In fact, if you tossed these coins once per second, you’d expect to get 100 heads once every [latex]2 \times 10^{22}[/latex] years. Disorder is vastly more likely than order.
Entropy and Disorder in Gases
These same statistical ideas apply to systems like gases. A small sample—say, 1.0 cm³ of gas at standard conditions—contains about [latex]2.7 \times 10^{19}[/latex] atoms. Each atom can occupy many possible microstates.
The most probable macrostate for a gas is a random distribution of atoms with a Maxwell-Boltzmann distribution of speeds and directions. A highly ordered state (all atoms in one corner) is technically possible but so unlikely that we consider it impossible. See Figure 114.2.
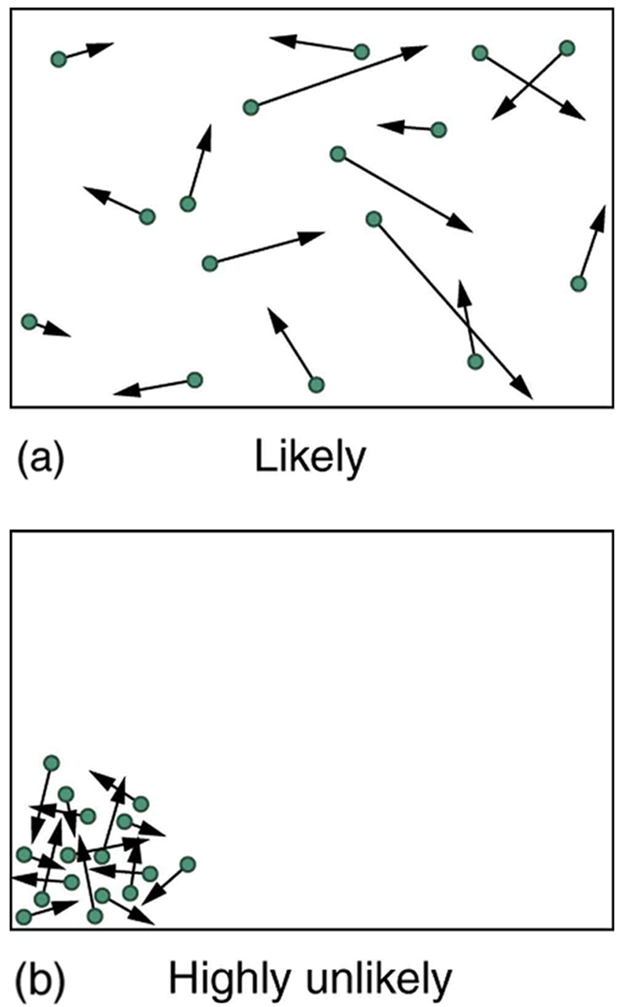
You could temporarily reduce entropy by compressing the gas into one corner (with energy input), but it will spontaneously return to a disordered state, increasing entropy overall. This is a key idea of the second law of thermodynamics.
The Boltzmann Entropy Formula
The Austrian physicist Ludwig Boltzmann showed that the entropy of a macrostate is related to the number of microstates:
Where:
- [latex]S[/latex] is entropy,
- [latex]k = 1.38 \times 10^{-23} \ \text{J/K}[/latex] is Boltzmann’s constant,
- [latex]W[/latex] is the number of microstates.
This formula links entropy to probability. Systems naturally move toward macrostates with greater [latex]W[/latex] because they are more probable. This explains why entropy increases in real-world processes.
Example 114.1 Entropy Increases in a Coin Toss
Suppose you toss 100 coins starting with 60 heads and 40 tails, and you get the most likely result, 50 heads and 50 tails. What is the change in entropy?
Strategy
Noting that the number of microstates is labeled [latex]W[/latex] in Table 114.2 for the 100-coin toss, we can use [latex]\Delta S={S}_{\text{f}}-{S}_{\text{i}}=k\text{ln}{W}_{\text{f}}-k\text{ln}{W}_{\text{i}}[/latex] to calculate the change in entropy.
Solution
The change in entropy is
where the subscript i stands for the initial 60 heads and 40 tails state, and the subscript f for the final 50 heads and 50 tails state. Substituting the values for [latex]W[/latex] from Table 114.2 gives
Discussion
This increase in entropy means we have moved to a less orderly situation. It is not impossible for further tosses to produce the initial state of 60 heads and 40 tails, but it is less likely. There is about a 1 in 90 chance for that decrease in entropy ([latex]–2\text{.}7×{\text{10}}^{–\text{23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}[/latex]) to occur. If we calculate the decrease in entropy to move to the most orderly state, we get [latex]\Delta S=–\text{92}×{\text{10}}^{–\text{23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}[/latex]. There is about a [latex]1\text{ in }{\text{10}}^{\text{30}}[/latex] chance of this change occurring. So while very small decreases in entropy are unlikely, slightly greater decreases are impossibly unlikely. These probabilities imply, again, that for a macroscopic system, a decrease in entropy is impossible. For example, for heat transfer to occur spontaneously from 1.00 kg of [latex]0º\text{C}[/latex] ice to its [latex]0º\text{C}[/latex] environment, there would be a decrease in entropy of [latex]1\text{.}\text{22}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{J/K}[/latex]. Given that a [latex]\Delta S{\text{ of 10}}^{–\text{21}}\phantom{\rule{0.25em}{0ex}}\text{J/K}[/latex] corresponds to about a [latex]1\text{ in }{\text{10}}^{\text{30}}[/latex] chance, a decrease of this size ([latex]{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{J/K}[/latex]) is an utter impossibility. Even for a milligram of melted ice to spontaneously refreeze is impossible.
Problem-Solving Strategies for Entropy
- Examine the situation to determine if entropy is involved.
- Identify the system of interest and draw a labeled diagram of the system showing energy flow.
- Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
- Make a list of what is given or can be inferred from the problem as stated (identify the knowns). You must carefully identify the heat transfer, if any, and the temperature at which the process takes place. It is also important to identify the initial and final states.
- Solve the appropriate equation for the quantity to be determined (the unknown). Note that the change in entropy can be determined between any states by calculating it for a reversible process.
- Substitute the known values, along with their units, into the appropriate equation, and obtain numerical solutions complete with units.
- Evaluate the reasonableness of your answer. For example, total entropy should increase for any real process or be constant for a reversible process. Disordered states should be more probable and have greater entropy than ordered states.
Section Summary
- Disorder is far more likely than order, as demonstrated by statistical analysis.
- The entropy of a system in a given state (macrostate) is given by:
[latex]S = k \ln W[/latex]
where:
[latex]k = 1.38 \times 10^{-23} \ \text{J/K}[/latex]is Boltzmann’s constant, and [latex]\ln W[/latex] is the natural logarithm of the number of microstates [latex]W[/latex] associated with the macrostate.
Conceptual Questions
- Explain why a building made of bricks has smaller entropy than the same bricks in a disorganized pile. Do this by considering the number of ways that each could be formed (the number of microstates in each macrostate).
Problem Exercises
- Using Table 114.2, verify the contention that if you toss 100 coins each second, you can expect to get 100 heads or 100 tails once in [latex]2×{\text{10}}^{\text{22}}[/latex] years; calculate the time to two-digit accuracy.
- What percent of the time will you get something in the range from 60 heads and 40 tails through 40 heads and 60 tails when tossing 100 coins? The total number of microstates in that range is [latex]1\text{.}\text{22}×{\text{10}}^{\text{30}}[/latex]. (Consult Table 114.2.)(a) If tossing 100 coins, how many ways (microstates) are there to get the three most likely macrostates of 49 heads and 51 tails, 50 heads and 50 tails, and 51 heads and 49 tails? (b) What percent of the total possibilities is this? (Consult Table 114.2.)
- (a) What is the change in entropy if you start with 100 coins in the 45 heads and 55 tails macrostate, toss them, and get 51 heads and 49 tails? (b) What if you get 75 heads and 25 tails? (c) How much more likely is 51 heads and 49 tails than 75 heads and 25 tails? (d) Does either outcome violate the second law of thermodynamics?
- (a) What is the change in entropy if you start with 10 coins in the 5 heads and 5 tails macrostate, toss them, and get 2 heads and 8 tails? (b) How much more likely is 5 heads and 5 tails than 2 heads and 8 tails? (Take the ratio of the number of microstates to find out.) (c) If you were betting on 2 heads and 8 tails would you accept odds of 252 to 45? Explain why or why not.
Table 114.3 10-Coin Toss Macrostate Number of Microstates (W) Heads Tails 10 0 1 9 1 10 8 2 45 7 3 120 6 4 210 5 5 252 4 6 210 3 7 120 2 8 45 1 9 10 0 10 1 Total: 1024 - (a) If you toss 10 coins, what percent of the time will you get the three most likely macrostates (6 heads and 4 tails, 5 heads and 5 tails, 4 heads and 6 tails)? (b) You can realistically toss 10 coins and count the number of heads and tails about twice a minute. At that rate, how long will it take on average to get either 10 heads and 0 tails or 0 heads and 10 tails?
- (a) Construct a table showing the macrostates and all of the individual microstates for tossing 6 coins. (Use Table 114.3) as a guide.) (b) How many macrostates are there? (c) What is the total number of microstates? (d) What percent chance is there of tossing 5 heads and 1 tail? (e) How much more likely are you to toss 3 heads and 3 tails than 5 heads and 1 tail? (Take the ratio of the number of microstates to find out.)
- In an air conditioner, 12.65 MJ of heat transfer occurs from a cold environment in 1.00 h. (a) What mass of ice melting would involve the same heat transfer? (b) How many hours of operation would be equivalent to melting 900 kg of ice? (c) If ice costs 20 cents per kg, do you think the air conditioner could be operated more cheaply than by simply using ice? Describe in detail how you evaluate the relative costs.
Glossary
- macrostate
- an overall property of a system
- microstate
- each sequence within a larger macrostate
- statistical analysis
- using statistics to examine data, such as counting microstates and macrostates
an overall property of a system
each sequence within a larger macrostate
using statistics to examine data, such as counting microstates and macrostates

