Heat and Heat Transfer Methods
106 Radiation
Learning Objectives
- Describe the process of heat transfer by radiation.
- Explain how color, surface texture, and temperature affect thermal radiation.
Have you ever felt the warmth of the Sun on your skin, even on a cool day? Or sensed heat coming from a campfire even when you’re sitting at a distance? These are everyday examples of heat transfer by radiation. Unlike conduction or convection, radiation does not require a medium. Instead, thermal energy is transferred through electromagnetic waves, which can move through empty space.
This type of energy transfer plays a crucial role in biological systems. For example, human skin can sense and absorb infrared radiation, which contributes to our perception of warmth. Radiation is also responsible for regulating body temperature by allowing heat to escape from the skin. On a broader scale, Earth’s climate system depends heavily on the balance between incoming radiation from the Sun and outgoing infrared radiation emitted by the surface.

Understanding Thermal Radiation
Thermal radiation spans a wide range of the electromagnetic spectrum, including infrared, visible light, and even ultraviolet. The wavelength of emitted radiation is closely related to the object’s temperature: hotter objects emit radiation at shorter wavelengths and higher intensities.
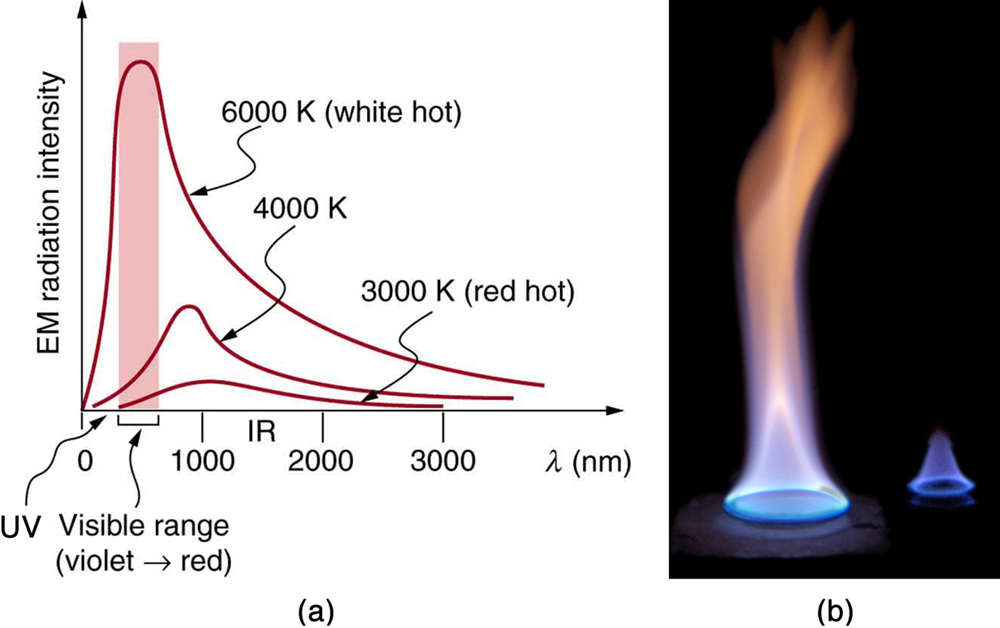
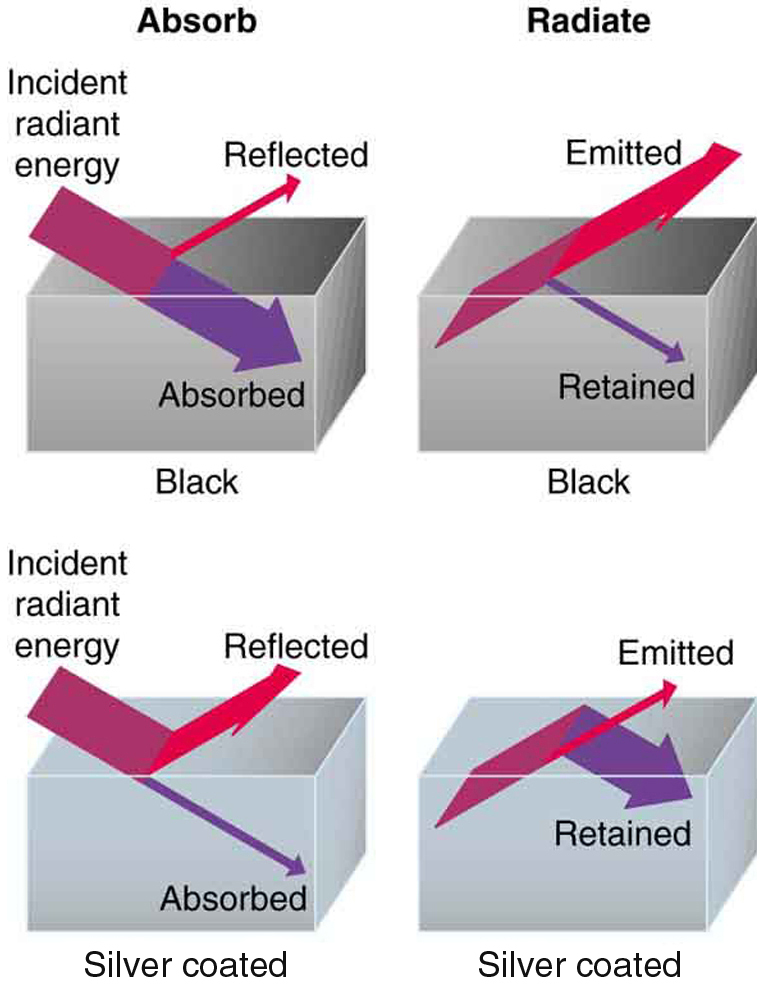
Absorbers and Emitters
Every object emits and absorbs radiation, but the effectiveness of this process depends on several properties—especially color and surface texture. Black objects are excellent absorbers and emitters, while white or reflective objects are poor at both. This is why darker surfaces heat up faster under sunlight and cool down more quickly at night.

Radiation in Biology and Health
Human skin is a remarkably efficient absorber and emitter of infrared radiation, with an emissivity of approximately 0.97. This makes it possible to detect temperature variations on the body’s surface using thermography, which is useful in medical diagnostics and biological research. Radiative cooling is also critical for maintaining homeostasis, particularly in warm environments where convection and conduction are less effective.
The Stefan-Boltzmann Law
The rate of energy emission by radiation is described by the Stefan-Boltzmann law:
Where:
- [latex]\frac{Q}{t}[/latex] is the radiative heat transfer rate
- [latex]\sigma = 5.67 \times 10^{-8} \ \text{J/s}\cdot \text{m}^2\cdot \text{K}^4[/latex] is the Stefan-Boltzmann constant
- [latex]e[/latex] is the emissivity of the object (ranges from 0 to 1)
- [latex]A[/latex] is the surface area
- [latex]T[/latex] is the absolute temperature in kelvin
This equation shows that radiation increases dramatically with temperature. A small rise in body temperature can result in a significant increase in radiative heat loss, which is crucial for thermal regulation in mammals and birds.

Net Radiative Heat Transfer
In most real situations, objects emit and absorb radiation at the same time. The net heat transfer depends on the temperature difference between the object and its surroundings:
Where:
- [latex]T_2[/latex] is the temperature of the environment
- [latex]T_1[/latex] is the temperature of the object
When the surroundings are hotter than the object ([latex]T_2 > T_1[/latex]), the object gains heat by radiation. This is relevant in biological and ecological contexts such as heat exposure in desert environments or greenhouse warming.
Take-Home Experiment: Temperature in the Sun
Place a thermometer in direct sunlight. First shield it with aluminum foil and record the temperature. Then remove the shield and observe the increase. Try wrapping the thermometer with a cloth dampened in nail polish remover and observe again. What does this tell you about radiation and evaporation?
Example 106.1 Calculate the Net Heat Transfer of a Person: Heat Transfer by Radiation
What is the rate of heat transfer by radiation, with an unclothed person standing in a dark room whose ambient temperature is [latex]\text{22}\text{.}0º\text{C}[/latex]. The person has a normal skin temperature of [latex]\text{33}\text{.}0º\text{C}[/latex] and a surface area of [latex]1\text{.}\text{50}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex]. The emissivity of skin is 0.97 in the infrared, where the radiation takes place.
Strategy
We can solve this by using the equation for the rate of radiative heat transfer.
Solution
Insert the temperatures values [latex]{T}_{2}=\text{295 K}[/latex] and [latex]{T}_{1}=\text{306 K}[/latex], so that
Discussion
This value is a significant rate of heat transfer to the environment (note the minus sign), considering that a person at rest may produce energy at the rate of 125 W and that conduction and convection will also be transferring energy to the environment. Indeed, we would probably expect this person to feel cold. Clothing significantly reduces heat transfer to the environment by many methods, because clothing slows down both conduction and convection, and has a lower emissivity (especially if it is white) than skin.
Radiative Heat Transfer and the Earth’s Energy Balance
The Earth receives nearly all of its energy through radiation from the Sun. Since the Sun has a much higher surface temperature than Earth, the net energy flow is from the Sun to the Earth. However, the actual rate of energy transfer is lower than predicted by the radiative heat transfer equation, because the Sun does not occupy the entire sky from the Earth’s perspective.
On average, Earth’s emissivity is approximately 0.65, but this value varies due to changing cloud coverage, which reflects a significant portion of incoming solar radiation. This leads to a form of negative feedback: warmer temperatures cause more water to evaporate, forming clouds that reflect additional sunlight, thereby reducing the temperature.
The greenhouse effect is closely tied to how Earth’s emissivity changes with radiation wavelength. It is a natural and essential process that helps maintain the Earth’s temperature at life-sustaining levels. While Earth emits infrared radiation due to its lower temperature, much of that radiation is absorbed by gases such as carbon dioxide ([latex]{\text{CO}}_{2}[/latex]) and water vapor ([latex]{\text{H}}_{2}\text{O}[/latex]) in the atmosphere. These gases then re-emit the energy back toward Earth or space. This re-radiation raises Earth’s surface temperature by roughly [latex]\text{40º}\text{C}[/latex] compared to what it would be in the absence of an atmosphere.
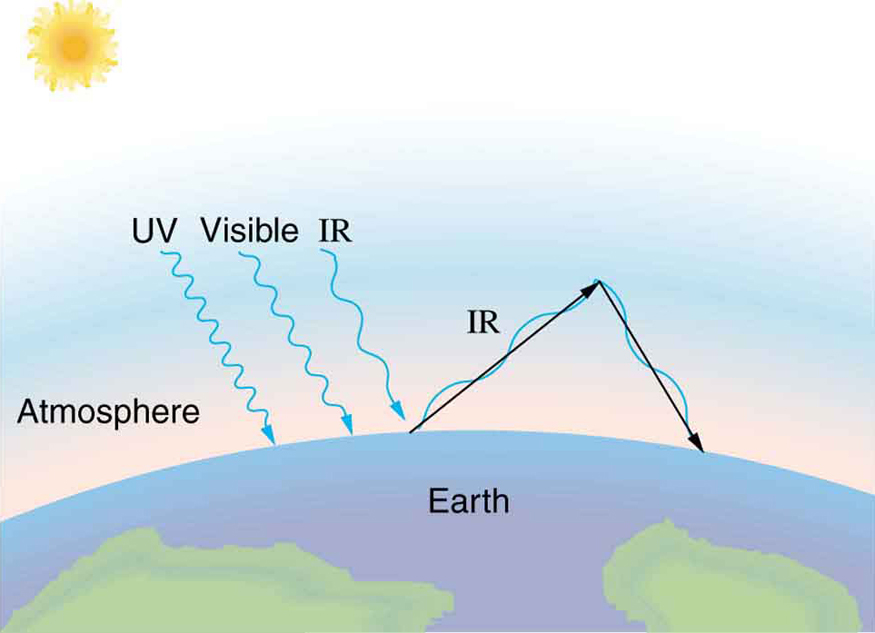
The greenhouse effect plays a central role in modern discussions of climate change. Increased emissions of greenhouse gases—primarily from fossil fuel combustion and agriculture—are contributing to global warming. Climate changes may bring more severe storms, altered precipitation patterns, biodiversity loss in rainforests, and rising sea levels due to polar ice melt.
Energy-Efficient Homes and the Greenhouse Effect
Heating and cooling account for a major portion of household energy consumption. Environmentally friendly home design emphasizes reducing the need for active heating and cooling. This can be achieved by using insulating materials, placing windows to take advantage of solar radiation, and promoting passive convection. Some homes are even designed to be zero-energy homes, consuming no net energy over the course of a year, even in regions with extreme seasonal temperatures.

Heat Radiation into Cold Space
In contrast to incoming solar energy, the Earth radiates heat into outer space, which is extremely cold—about [latex]3\,\text{K}[/latex] (or [latex]-454^\circ\text{F}[/latex]). On clear nights, without cloud cover, heat loss can be rapid enough to cause frost, even in otherwise warm climates. Clouds play a dual role: they reduce heat loss at night and reflect sunlight during the day, due to their lower emissivity compared to oceans and land.
Check Your Understanding
Question: How does the rate of radiated heat change for a body heated from [latex]20^\circ\text{C}[/latex] to [latex]40^\circ\text{C}[/latex]?
Answer: Radiated heat is proportional to the fourth power of the absolute temperature. Converting to Kelvin: [latex]T_1 = 293\,\text{K}[/latex] and [latex]T_2 = 313\,\text{K}[/latex]. The heat transfer rate increases by approximately 30%.
Career Connection: Energy Conservation Consultant
With rising energy costs, professionals who analyze and reduce home energy use are in demand. Energy conservation consultants assess how homes gain or lose heat and recommend improvements such as insulation upgrades, window placements, and ventilation strategies. Their work supports both cost savings and environmental sustainability.
Problem-Solving Strategies: Methods of Heat Transfer
- Identify the type of heat transfer: Is it conduction, convection, or radiation?
- Determine the unknowns: What are you solving for?
- List the known quantities: Extract data from the problem.
- Choose the relevant equation:
- Conduction: [latex]\frac{Q}{t}=\frac{kA(T_2 - T_1)}{d}[/latex]
- Convection: Use [latex]Q = mc\Delta T[/latex]; if phase change is involved, use [latex]Q = mL_f[/latex] or [latex]Q = mL_v[/latex]
- Radiation: [latex]\frac{Q_{\text{net}}}{t} = \sigma eA(T_2^4 - T_1^4)[/latex]
- Plug in values and solve.
- Evaluate your answer: Does it make physical sense?
Summary
- Radiation transfers energy via electromagnetic waves.
- Radiative heat transfer depends on the surface area and the fourth power of absolute temperature:
where [latex]\sigma = 5.67 \times 10^{-8}\,\text{J/s}\cdot \text{m}^2\cdot \text{K}^4[/latex] is the Stefan-Boltzmann constant, and [latex]e[/latex] is the object’s emissivity. The net heat transfer between two temperatures is given by:
Conceptual Questions
- When watching a daytime circus in a large, dark-colored tent, you sense significant heat transfer from the tent. Explain why this occurs.
- Satellites designed to observe the radiation from cold (3 K) dark space have sensors that are shaded from the Sun, Earth, and Moon and that are cooled to very low temperatures. Why must the sensors be at low temperature?
- Why are cloudy nights generally warmer than clear ones?
- Why are thermometers that are used in weather stations shielded from the sunshine? What does a thermometer measure if it is shielded from the sunshine and also if it is not?
- On average, would Earth be warmer or cooler without the atmosphere? Explain your answer.
Problems & Exercises
- At what net rate does heat radiate from a [latex]\text{275}{\text{-m}}^{2}[/latex] black roof on a night when the roof’s temperature is [latex]\text{30.}0º\text{C}[/latex] and the surrounding temperature is [latex]\text{15.}0º\text{C}[/latex]? The emissivity of the roof is 0.900.
- (a) Cherry-red embers in a fireplace are at [latex]\text{850º}\text{C}[/latex] and have an exposed area of [latex]0\text{.}\text{200}\phantom{\rule{0.25em}{0ex}}{\text{ m}}^{2}[/latex] and an emissivity of 0.980. The surrounding room has a temperature of [latex]\text{18}\text{.}0º\text{C}[/latex]. If 50% of the radiant energy enters the room, what is the net rate of radiant heat transfer in kilowatts? (b) Does your answer support the contention that most of the heat transfer into a room by a fireplace comes from infrared radiation?
- Radiation makes it impossible to stand close to a hot lava flow. Calculate the rate of heat transfer by radiation from [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{ m}}^{2}[/latex] of [latex]\text{1200º}\text{C}[/latex] fresh lava into [latex]\text{30}\text{.}0º\text{C}[/latex] surroundings, assuming lava’s emissivity is 1.00.
- (a) Calculate the rate of heat transfer by radiation from a car radiator at [latex]110°\text{C}[/latex] into a [latex]50.0º\text{C}[/latex] environment, if the radiator has an emissivity of 0.750 and a [latex]1.20{\mathrm{-m}}^{2}[/latex] surface area. (b) Is this a significant fraction of the heat transfer by an automobile engine? To answer this, assume a horsepower of [latex]200\phantom{\rule{0.25em}{0ex}}\text{hp}\phantom{\rule{0.25em}{0ex}}\left(1.5\phantom{\rule{0.25em}{0ex}}\text{kW}\right)[/latex] and the efficiency of automobile engines as 25%.
- Find the net rate of heat transfer by radiation from a skier standing in the shade, given the following. She is completely clothed in white (head to foot, including a ski mask), the clothes have an emissivity of 0.200 and a surface temperature of [latex]\text{10}\text{.}0º\text{C}[/latex], the surroundings are at [latex]-\text{15}\text{.}\text{0ºC}[/latex], and her surface area is [latex]1\text{.}\text{60}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex].
- Suppose you walk into a sauna that has an ambient temperature of [latex]\text{50}\text{.0ºC}[/latex]. (a) Calculate the rate of heat transfer to you by radiation given your skin temperature is [latex]\text{37}\text{.0ºC}[/latex], the emissivity of skin is 0.98, and the surface area of your body is [latex]1\text{.50}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex]. (b) If all other forms of heat transfer are balanced (the net heat transfer is zero), at what rate will your body temperature increase if your mass is 75.0 kg?
- Thermography is a technique for measuring radiant heat and detecting variations in surface temperatures that may be medically, environmentally, or militarily meaningful.(a) What is the percent increase in the rate of heat transfer by radiation from a given area at a temperature of [latex]\text{34.0ºC}[/latex] compared with that at [latex]\text{33}\text{.}\text{0ºC}[/latex], such as on a person’s skin? (b) What is the percent increase in the rate of heat transfer by radiation from a given area at a temperature of [latex]\text{34.0ºC}[/latex] compared with that at [latex]\text{20.0ºC}[/latex], such as for warm and cool automobile hoods?
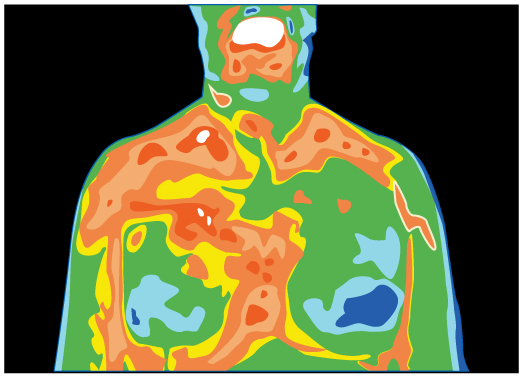
Figure 106.8: Artist’s rendition of a thermograph of a patient’s upper body, showing the distribution of heat represented by different colors. - The Sun radiates like a perfect black body with an emissivity of exactly 1. (a) Calculate the surface temperature of the Sun, given that it is a sphere with a [latex]7\text{.}\text{00}×{\text{10}}^{8}\text{-m}[/latex] radius that radiates [latex]3\text{.}\text{80}×{\text{10}}^{\text{26}}\text{ W}[/latex] into 3-K space. (b) How much power does the Sun radiate per square meter of its surface? (c) How much power in watts per square meter is that value at the distance of Earth, [latex]1\text{.}\text{50}×{\text{10}}^{\text{11}}\text{ m}[/latex] away? (This number is called the solar constant.)
- A large body of lava from a volcano has stopped flowing and is slowly cooling. The interior of the lava is at [latex]\text{1200ºC}[/latex], its surface is at [latex]\text{450ºC}[/latex], and the surroundings are at [latex]\text{27}\text{.}\text{0ºC}[/latex]. (a) Calculate the rate at which energy is transferred by radiation from [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{ m}}^{2}[/latex] of surface lava into the surroundings, assuming the emissivity is 1.00. (b) Suppose heat conduction to the surface occurs at the same rate. What is the thickness of the lava between the [latex]\text{450ºC}[/latex] surface and the [latex]\text{1200ºC}[/latex] interior, assuming that the lava’s conductivity is the same as that of brick?
- Calculate the temperature the entire sky would have to be in order to transfer energy by radiation at [latex]\text{1000}\phantom{\rule{0.25em}{0ex}}{\text{W/m}}^{2}[/latex] —about the rate at which the Sun radiates when it is directly overhead on a clear day. This value is the effective temperature of the sky, a kind of average that takes account of the fact that the Sun occupies only a small part of the sky but is much hotter than the rest. Assume that the body receiving the energy has a temperature of [latex]\text{27}\text{.}\text{0ºC}[/latex].
- (a) A shirtless rider under a circus tent feels the heat radiating from the sunlit portion of the tent. Calculate the temperature of the tent canvas based on the following information: The shirtless rider’s skin temperature is [latex]\text{34}\text{.}\text{0ºC}[/latex] and has an emissivity of 0.970. The exposed area of skin is [latex]0\text{.}\text{400}\phantom{\rule{0.25em}{0ex}}{\text{ m}}^{2}[/latex]. He receives radiation at the rate of 20.0 W—half what you would calculate if the entire region behind him was hot. The rest of the surroundings are at [latex]\text{34}\text{.}\text{0ºC}[/latex]. (b) Discuss how this situation would change if the sunlit side of the tent was nearly pure white and if the rider was covered by a white tunic.
- Integrated Concepts One [latex]\text{30}\text{.}\text{0ºC}[/latex] day the relative humidity is [latex]\text{75}\text{.}\text{0%}[/latex], and that evening the temperature drops to [latex]\text{20}\text{.}\text{0ºC}[/latex], well below the dew point. (a) How many grams of water condense from each cubic meter of air? (b) How much heat transfer occurs by this condensation? (c) What temperature increase could this cause in dry air?
- Integrated Concepts Large meteors sometimes strike the Earth, converting most of their kinetic energy into thermal energy. (a) What is the kinetic energy of a [latex]{\text{10}}^{9}\text{ kg}[/latex] meteor moving at 25.0 km/s? (b) If this meteor lands in a deep ocean and [latex]\text{80%}[/latex] of its kinetic energy goes into heating water, how many kilograms of water could it raise by [latex]5\text{.}\text{0ºC?}[/latex] (c) Discuss how the energy of the meteor is more likely to be deposited in the ocean and the likely effects of that energy.
- Integrated Concepts Frozen waste from airplane toilets has sometimes been accidentally ejected at high altitude. Ordinarily it breaks up and disperses over a large area, but sometimes it holds together and strikes the ground. Calculate the mass of [latex]\text{0ºC}[/latex] ice that can be melted by the conversion of kinetic and gravitational potential energy when a [latex]\text{20}\text{.0 kg}[/latex] piece of frozen waste is released at 12.0 km altitude while moving at 250 m/s and strikes the ground at 100 m/s (since less than 20.0 kg melts, a significant mess results).
- Integrated Concepts (a) A large electrical power facility produces 1600 MW of “waste heat,” which is dissipated to the environment in cooling towers by warming air flowing through the towers by [latex]5\text{.}\text{00ºC}[/latex]. What is the necessary flow rate of air in [latex]{\text{m}}^{3}\text{/s}[/latex]? (b) Is your result consistent with the large cooling towers used by many large electrical power plants?
- Integrated Concepts (a) Suppose you start a workout on a Stairmaster, producing power at the same rate as climbing 116 stairs per minute. Assuming your mass is 76.0 kg and your efficiency is [latex]\text{20}\text{.}\text{0%}[/latex], how long will it take for your body temperature to rise [latex]1\text{.}\text{00ºC}[/latex] if all other forms of heat transfer in and out of your body are balanced? (b) Is this consistent with your experience in getting warm while exercising?
- Integrated Concepts A 76.0-kg person suffering from hypothermia comes indoors and shivers vigorously. How long does it take the heat transfer to increase the person’s body temperature by [latex]2\text{.}\text{00ºC}[/latex] if all other forms of heat transfer are balanced?
- Integrated Concepts In certain large geographic regions, the underlying rock is hot. Wells can be drilled and water circulated through the rock for heat transfer for the generation of electricity. (a) Calculate the heat transfer that can be extracted by cooling [latex]1\text{.00}\phantom{\rule{0.25em}{0ex}}{\text{ km}}^{3}[/latex] of granite by [latex]\text{100ºC}[/latex]. (b) How long will it take for heat transfer at the rate of 300 MW, assuming no heat transfers back into the [latex]1\text{.00}\phantom{\rule{0.25em}{0ex}}{\text{km}}^{3}[/latex] of rock by its surroundings?
- Integrated Concepts Heat transfers from your lungs and breathing passages by evaporating water. (a) Calculate the maximum number of grams of water that can be evaporated when you inhale 1.50 L of [latex]37º\text{C}[/latex] air with an original relative humidity of 40.0%. (Assume that body temperature is also [latex]37º\text{C}[/latex].) (b) How many joules of energy are required to evaporate this amount? (c) What is the rate of heat transfer in watts from this method, if you breathe at a normal resting rate of 10.0 breaths per minute?
- Integrated Concepts (a) What is the temperature increase of water falling 55.0 m over Niagara Falls? (b) What fraction must evaporate to keep the temperature constant?
- Integrated Concepts Hot air rises because it has expanded. It then displaces a greater volume of cold air, which increases the buoyant force on it. (a) Calculate the ratio of the buoyant force to the weight of [latex]50.0º\text{C}[/latex] air surrounded by [latex]20.0º\text{C}[/latex] air. (b) What energy is needed to cause [latex]1.00\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}[/latex] of air to go from [latex]20.0º\text{C}[/latex] to [latex]50.0º\text{C}[/latex]? (c) What gravitational potential energy is gained by this volume of air if it rises 1.00 m? Will this cause a significant cooling of the air?
- Unreasonable Results (a) What is the temperature increase of an 80.0 kg person who consumes 2500 kcal of food in one day with 95.0% of the energy transferred as heat to the body? (b) What is unreasonable about this result? (c) Which premise or assumption is responsible?
- Unreasonable Results A slightly deranged Arctic inventor surrounded by ice thinks it would be much less mechanically complex to cool a car engine by melting ice on it than by having a water-cooled system with a radiator, water pump, antifreeze, and so on. (a) If [latex]\text{80}\text{.}\text{0%}[/latex] of the energy in 1.00 gal of gasoline is converted into “waste heat” in a car engine, how many kilograms of [latex]\text{0ºC}[/latex] ice could it melt? (b) Is this a reasonable amount of ice to carry around to cool the engine for 1.00 gal of gasoline consumption? (c) What premises or assumptions are unreasonable?
- Unreasonable Results (a) Calculate the rate of heat transfer by conduction through a window with an area of [latex]1\text{.00}\phantom{\rule{0.25em}{0ex}}{\text{ m}}^{2}[/latex] that is 0.750 cm thick, if its inner surface is at [latex]\text{22.0ºC}[/latex] and its outer surface is at [latex]\text{35.0ºC}[/latex]. (b) What is unreasonable about this result? (c) Which premise or assumption is responsible?
- Unreasonable Results A meteorite 1.20 cm in diameter is so hot immediately after penetrating the atmosphere that it radiates 20.0 kW of power. (a) What is its temperature, if the surroundings are at [latex]\text{20.0ºC}[/latex] and it has an emissivity of 0.800? (b) What is unreasonable about this result? (c) Which premise or assumption is responsible?
- Construct Your Own Problem Consider a new model of commercial airplane having its brakes tested as a part of the initial flight permission procedure. The airplane is brought to takeoff speed and then stopped with the brakes alone. Construct a problem in which you calculate the temperature increase of the brakes during this process. You may assume most of the kinetic energy of the airplane is converted to thermal energy in the brakes and surrounding materials, and that little escapes. Note that the brakes are expected to become so hot in this procedure that they ignite and, in order to pass the test, the airplane must be able to withstand the fire for some time without a general conflagration.
- Construct Your Own Problem Consider a person outdoors on a cold night. Construct a problem in which you calculate the rate of heat transfer from the person by all three heat transfer methods. Make the initial circumstances such that at rest the person will have a net heat transfer and then decide how much physical activity of a chosen type is necessary to balance the rate of heat transfer. Among the things to consider are the size of the person, type of clothing, initial metabolic rate, sky conditions, amount of water evaporated, and volume of air breathed. Of course, there are many other factors to consider and your instructor may wish to guide you in the assumptions made as well as the detail of analysis and method of presenting your results.
Glossary
- emissivity
- measure of how well an object radiates
- greenhouse effect
- warming of the Earth that is due to gases such as carbon dioxide and methane that absorb infrared radiation from the Earth’s surface and reradiate it in all directions, thus sending a fraction of it back toward the surface of the Earth
- net rate of heat transfer by radiation
- is
[latex]\frac{{Q}_{\text{net}}}{t}=\sigma eA\left({T}_{2}^{4}-{T}_{1}^{4}\right)[/latex]
- radiation
- energy transferred by electromagnetic waves directly as a result of a temperature difference
- Stefan-Boltzmann law of radiation
- [latex]\frac{Q}{t}=\sigma eA{T}^{4},[/latex] where [latex]\sigma[/latex] is the Stefan-Boltzmann constant, [latex]A[/latex] is the surface area of the object, [latex]T[/latex] is the absolute temperature, and [latex]e[/latex] is the emissivity
measure of how well an object radiates
warming of the Earth that is due to gases such as carbon dioxide and methane that absorb infrared radiation from the Earth’s surface and reradiate it in all directions, thus sending a fraction of it back toward the surface of the Earth
is
[latex]\frac{{Q}_{\text{net}}}{t}=\sigma eA\left({T}_{2}^{4}-{T}_{1}^{4}\right)[/latex]
heat transfer which occurs when microwaves, infrared radiation, visible light, or other electromagnetic radiation is emitted or absorbed
[latex]\frac{Q}{t}=\sigma eA{T}^{4},[/latex] where [latex]\sigma[/latex] is the Stefan-Boltzmann constant, [latex]A[/latex] is the surface area of the object, [latex]T[/latex] is the absolute temperature, and [latex]e[/latex] is the emissivity

