Previously, we defined pressure as force per unit area and temperature as what a thermometer reads. But we can gain a much deeper understanding of both pressure and temperature through the kinetic theory of gases, which assumes that atoms and molecules are in constant, random motion.

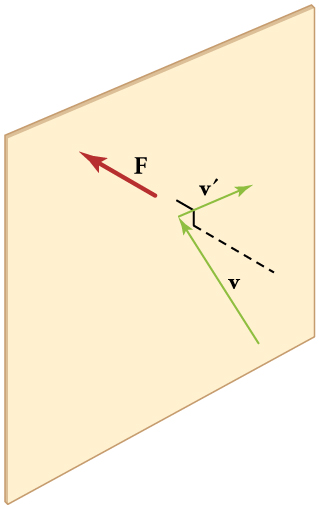
As illustrated in Figure 96.1, gas molecules colliding with the walls of a container exert force. Since countless collisions occur every second, the resulting force averaged over the surface area creates a measurable pressure. This pressure increases with the number of molecules and with their speed. In fact, we can derive an expression that links pressure to the average speed of the molecules:

Here, [latex]P[/latex] is the pressure, [latex]V[/latex] is the volume, [latex]N[/latex] is the number of molecules, [latex]m[/latex] is the mass of each molecule, and [latex]\overline{v^2}[/latex] is the average of the square of the molecular speeds. This connects microscopic motion to macroscopic quantities.

Recall the molecular version of the ideal gas law:

By setting the right-hand sides of these two expressions equal, we find:

Things Great and Small: Microscopic Origin of Pressure

Figure 96.2 visualizes gas molecules bouncing around in a container. When a molecule strikes the wall, its velocity in the direction perpendicular to the wall is reversed, generating force through momentum transfer. Averaging the effects of these collisions gives rise to the pressure we observe macroscopically.

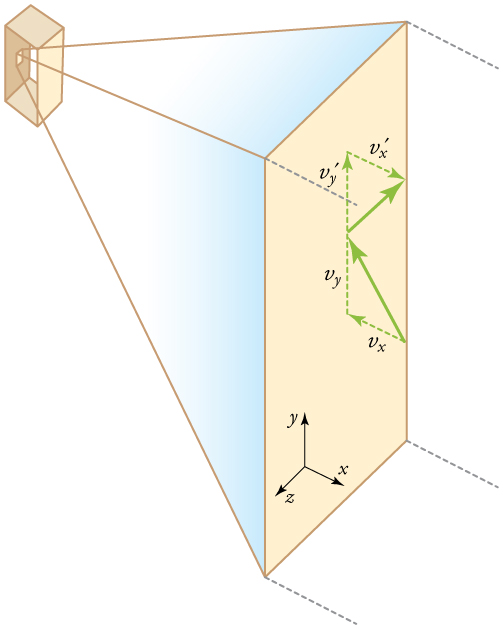
Let’s derive the expression for pressure from the collision mechanics:

The change in momentum for a single molecule bouncing off the wall is:

The average time between collisions with the same wall is [latex]\Delta t = \frac{2l}{v_x}[/latex], so the average force from one molecule is:

Multiplying by the number of molecules [latex]N[/latex] and averaging over all velocities:

Using the fact that in a gas with random motion:

we get:

Since pressure is force divided by area and volume is [latex]V = Al[/latex], we arrive at:

Translational Kinetic Energy and Temperature

We can now link the average kinetic energy of a gas molecule to the temperature of the gas. Starting from:

Divide both sides by [latex]N[/latex] and multiply by [latex]\frac{3}{2}[/latex] to get:

This equation defines thermal energy as the average translational kinetic energy of a molecule in a gas. It also provides a molecular-level definition of temperature.

Root-Mean-Square Speed

The root-mean-square (rms) speed, [latex]v_{\text{rms}}[/latex], is the square root of the average of the square of the molecular speed. Rearranging the kinetic energy expression, we find:

This expression allows us to calculate the average speed of gas molecules based on the temperature and molecular mass, which is particularly important in biological systems involving gases such as oxygen, nitrogen, or carbon dioxide.

Example 96.1: Calculating Kinetic Energy and Speed of a Gas Molecule

(a) What is the average kinetic energy of a gas molecule at [latex]\text{20}\text{.}0\text{º}\text{C}[/latex] (room temperature)? (b) Find the rms speed of a nitrogen molecule [latex]\left({\text{N}}_{2}\right)[/latex] at this temperature.

Strategy for (a)

The known in the equation for the average kinetic energy is the temperature.

[latex]\overline{\text{KE}}=\frac{1}{2}m\overline{{v}^{2}}=\frac{3}{2}\text{kT}[/latex]

Before substituting values into this equation, we must convert the given temperature to kelvins. This conversion gives [latex]T=\left(\text{20}\text{.}0+\text{273}\right)\phantom{\rule{0.25em}{0ex}}\text{K = 293}\phantom{\rule{0.25em}{0ex}}\text{K}.[/latex]

Solution for (a)

The temperature alone is sufficient to find the average translational kinetic energy. Substituting the temperature into the translational kinetic energy equation gives

[latex]\overline{\text{KE}}=\frac{3}{2}\text{kT}=\frac{3}{2}\left(1\text{.}\text{38}×{\text{10}}^{-\text{23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}\right)\left(\text{293}\phantom{\rule{0.25em}{0ex}}\text{K}\right)=6\text{.}\text{07}×{\text{10}}^{-\text{21}}\phantom{\rule{0.25em}{0ex}}\text{J}\text{.}[/latex]

Strategy for (b)

Finding the rms speed of a nitrogen molecule involves a straightforward calculation using the equation

[latex]\sqrt{\overline{{v}^{2}}}={v}_{\text{rms}}=\sqrt{\frac{3\text{kT}}{m}},[/latex]

but we must first find the mass of a nitrogen molecule. Using the molecular mass of nitrogen [latex]{\text{N}}_{2}[/latex] from the periodic table,

[latex]m=\frac{2\left(\text{14}\text{.}\text{0067}\right)×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{kg/mol}}{6\text{.}\text{02}×{\text{10}}^{\text{23}}\phantom{\rule{0.25em}{0ex}}{\text{mol}}^{-1}}=4\text{.}\text{65}×{\text{10}}^{-\text{26}}\phantom{\rule{0.25em}{0ex}}\text{kg}\text{.}[/latex]

Solution for (b)

Substituting this mass and the value for [latex]k[/latex] into the equation for [latex]{v}_{\text{rms}}[/latex] yields

[latex]{v}_{\text{rms}}=\sqrt{\frac{3\text{kT}}{m}}=\sqrt{\frac{3\left(1\text{.}\text{38}×{\text{10}}^{–\text{23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}\right)\left(\text{293 K}\right)}{4\text{.}\text{65}×{\text{10}}^{\text{–26}}\phantom{\rule{0.25em}{0ex}}\text{kg}}}=\text{511}\phantom{\rule{0.25em}{0ex}}\text{m/s}\text{.}[/latex]

Discussion

Note that the average kinetic energy of the molecule is independent of the type of molecule. The average translational kinetic energy depends only on absolute temperature. The kinetic energy is very small compared to macroscopic energies, so that we do not feel when an air molecule is hitting our skin. The rms velocity of the nitrogen molecule is surprisingly large. These large molecular velocities do not yield macroscopic movement of air, since the molecules move in all directions with equal likelihood. The mean free path (the distance a molecule can move on average between collisions) of molecules in air is very small, and so the molecules move rapidly but do not get very far in a second. The high value for rms speed is reflected in the speed of sound, however, which is about 340 m/s at room temperature. The faster the rms speed of air molecules, the faster that sound vibrations can be transferred through the air. The speed of sound increases with temperature and is greater in gases with small molecular masses, such as helium. (See Figure 96.3 )

Making Connections: Historical Note—Kinetic Theory of Gases

The foundations of the kinetic theory of gases were laid by Daniel Bernoulli (1700–1782), a pioneer in fluid mechanics. Remarkably, Bernoulli developed this theory long before the modern atomic model of matter was fully established by John Dalton in the early 1800s. His early insights into the connection between molecular motion and pressure helped shape the modern understanding of gases.

Distribution of Molecular Speeds

Although individual gas molecules move randomly in both speed and direction, a gas composed of a large number of molecules exhibits a predictable pattern of molecular speeds. This pattern is described by the Maxwell-Boltzmann distribution, which was derived using kinetic theory and confirmed through experimental data.

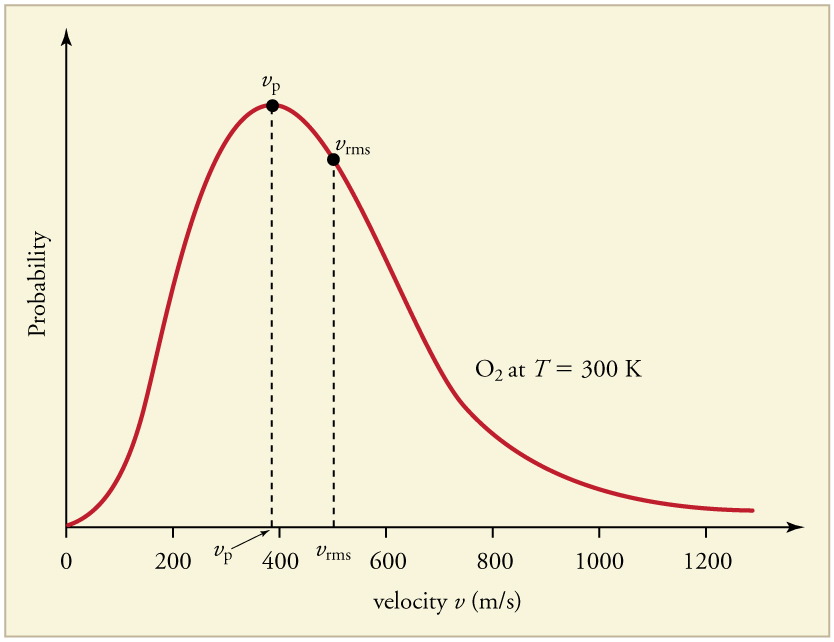
The distribution is asymmetric (aee Figure 96.4): most molecules cluster around the most probable speed [latex]v_{\text{p}}[/latex], while fewer have speeds much higher or lower than this value. The root-mean-square speed [latex]v_{\text{rms}}[/latex] is slightly higher than [latex]v_{\text{p}}[/latex] and represents the square root of the average of the squared speeds. As temperature increases, the entire speed distribution shifts to the right (toward higher speeds) and becomes broader like shown in Figure 96.5.

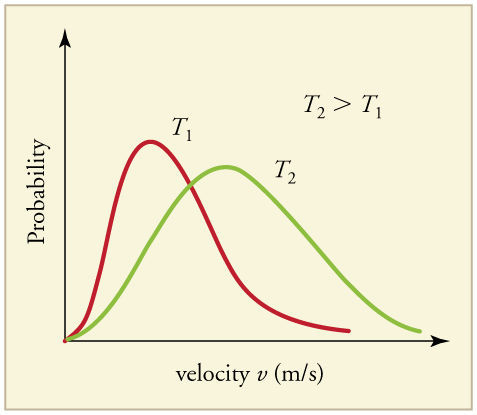
Biological relevance: This temperature dependence has important implications for the human body. At elevated body temperatures (such as during a fever), the molecules in our tissues, including water molecules in the respiratory tract and mucous membranes, move faster. This results in a higher rate of evaporation from moist surfaces such as the mouth and lungs. As a result, people often feel dry-mouthed or dehydrated during a fever, even if their water intake hasn’t changed.

Example 96.2: Calculating Temperature: Escape Velocity of Helium Atoms

In order to escape Earth’s gravity, an object near the top of the atmosphere (at an altitude of 100 km) must travel away from Earth at 11.1 km/s. This speed is called the escape velocity. At what temperature would helium atoms have an rms speed equal to the escape velocity?

Strategy

Identify the knowns and unknowns and determine which equations to use to solve the problem.

Solution

1. Identify the knowns: [latex]v[/latex] is the escape velocity, 11.1 km/s.
2. Identify the unknowns: We need to solve for temperature, [latex]T[/latex]. We also need to solve for the mass [latex]m[/latex] of the helium atom.
3. Determine which equations are needed.
   • To solve for mass [latex]m[/latex] of the helium atom, we can use information from the periodic table:
     [latex]m=\frac{\text{molar mass}}{\text{number of atoms per mole}}.[/latex]
   • To solve for temperature [latex]T[/latex], we can rearrange either
     [latex]\overline{\text{KE}}=\frac{1}{2}m\overline{{v}^{2}}=\frac{3}{2}\text{kT}[/latex]

     or

     [latex]\sqrt{\overline{{v}^{2}}}={v}_{\text{rms}}=\sqrt{\frac{3\text{kT}}{m}}[/latex]

     to yield

     [latex]T=\frac{m\overline{{v}^{2}}}{\text{3}k},[/latex]

     where [latex]k[/latex] is the Boltzmann constant and [latex]m[/latex] is the mass of a helium atom.

4. Plug the known values into the equations and solve for the unknowns.
   [latex]m=\frac{\text{molar mass}}{\text{number of atoms per mole}}=\frac{4\text{.}\text{0026}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{kg/mol}}{6\text{.}\text{02}×{\text{10}}^{\text{23}}\phantom{\rule{0.25em}{0ex}}\text{mol}}=6\text{.}\text{65}×{\text{10}}^{-\text{27}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex]
   [latex]T=\frac{\left(6\text{.}\text{65}×{\text{10}}^{-\text{27}}\phantom{\rule{0.25em}{0ex}}\text{kg}\right){\left(\text{11}\text{.}1×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)}^{2}}{3\left(1\text{.}\text{38}×{\text{10}}^{-\text{23}}\phantom{\rule{0.25em}{0ex}}\text{J/K}\right)}=1\text{.}\text{98}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{K}[/latex]

Discussion

This temperature is much higher than atmospheric temperature, which is approximately 250 K [latex](–\text{25}\text{º}\text{C}[/latex] or [latex]–\text{10}\text{º}\text{F})[/latex] at high altitude. Very few helium atoms are left in the atmosphere, but there were many when the atmosphere was formed. The reason for the loss of helium atoms is that there are a small number of helium atoms with speeds higher than Earth’s escape velocity even at normal temperatures. The speed of a helium atom changes from one instant to the next, so that at any instant, there is a small, but nonzero chance that the speed is greater than the escape speed and the molecule escapes from Earth’s gravitational pull. Heavier molecules, such as oxygen, nitrogen, and water (very little of which reach a very high altitude), have smaller rms speeds, and so it is much less likely that any of them will have speeds greater than the escape velocity. In fact, so few have speeds above the escape velocity that billions of years are required to lose significant amounts of the atmosphere. Figure 96.6 shows the impact of a lack of an atmosphere on the Moon. Because the gravitational pull of the Moon is much weaker, it has lost almost its entire atmosphere. The comparison between Earth and the Moon is discussed in this chapter’s Problems and Exercises.

Check Your Understanding

If you consider a very small object such as a grain of pollen, in a gas, then the number of atoms and molecules striking its surface would also be relatively small. Would the grain of pollen experience any fluctuations in pressure due to statistical fluctuations in the number of gas atoms and molecules striking it in a given amount of time?

Yes. Such fluctuations actually occur for a body of any size in a gas, but since the numbers of atoms and molecules are immense for macroscopic bodies, the fluctuations are a tiny percentage of the number of collisions, and the averages spoken of in this section vary imperceptibly. Roughly speaking the fluctuations are proportional to the inverse square root of the number of collisions, so for small bodies they can become significant. This was actually observed in the 19th century for pollen grains in water, and is known as the Brownian effect.

PhET Explorations: Gas Properties

Explore the molecular behavior of gases with this interactive simulation. You can pump gas molecules into a container and observe how their behavior changes when you:

• Increase or decrease the volume of the container
• Add or remove heat to change the temperature
• Adjust the gravitational field
• Introduce different types of gas particles

This tool allows you to directly measure temperature and pressure and see how they relate to other variables like volume and particle speed. It visually reinforces key ideas such as the kinetic theory of gases, thermal energy, and how microscopic motion translates into macroscopic properties like pressure and temperature.

This simulation is especially useful for understanding how energy changes at the molecular level can influence phenomena in biological systems—such as gas exchange in the lungs or temperature regulation in cells.

Section Summary

• Kinetic theory describes the behavior of gases, liquids, and solids based on the motion of atoms and molecules.
• Kinetic theory models matter as consisting of particles in continuous, random motion. For gases, this random motion explains properties like pressure and temperature.
• The ideal gas law can be expressed in molecular terms as:
  [latex]\text{PV} = \frac{1}{3} N m \overline{v^2}[/latex]

  where:

  • [latex]P[/latex] is the pressure (average force per unit area),
  • [latex]V[/latex] is the volume of the gas,
  • [latex]N[/latex] is the number of molecules,
  • [latex]m[/latex] is the mass of a molecule,
  • [latex]\overline{v^2}[/latex] is the average of the squared molecular speed.
• Thermal energy refers to the average translational kinetic energy of a gas particle and is defined as:
  [latex]\overline{\text{KE}} = \frac{1}{2} m \overline{v^2} = \frac{3}{2} k T[/latex]
• The temperature of a gas is directly proportional to the average kinetic energy of its atoms or molecules. This relationship provides a molecular definition of temperature.
• The root-mean-square (rms) speed of molecules in a gas is given by:
  [latex]v_{\text{rms}} = \sqrt{\overline{v^2}} = \sqrt{\frac{3kT}{m}}[/latex]
• Although individual molecular speeds are random, a gas of many molecules exhibits a predictable Maxwell-Boltzmann distribution of speeds. This distribution becomes broader and shifts to higher speeds as the temperature increases.

Conceptual Questions

13. How is momentum related to the pressure exerted by a gas? Explain on the atomic and molecular level, considering the behavior of atoms and molecules.

Problems & Exercises

39. Some incandescent light bulbs are filled with argon gas. What is [latex]{v}_{\text{rms}}[/latex] for argon atoms near the filament, assuming their temperature is 2500 K?
40. Average atomic and molecular speeds [latex]\left({v}_{\text{rms}}\right)[/latex] are large, even at low temperatures. What is [latex]{v}_{\text{rms}}[/latex] for helium atoms at 5.00 K, just one degree above helium’s liquefaction temperature?
41. (a) What is the average kinetic energy in joules of hydrogen atoms on the [latex]\text{5500}\text{º}\text{C}[/latex] surface of the Sun? (b) What is the average kinetic energy of helium atoms in a region of the solar corona where the temperature is [latex]6\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{K}[/latex]?
42. The escape velocity of any object from Earth is 11.2 km/s. (a) Express this speed in m/s and km/h. (b) At what temperature would oxygen molecules (molecular mass is equal to 32.0 g/mol) have an average velocity [latex]{v}_{\text{rms}}[/latex] equal to Earth’s escape velocity of 11.1 km/s?
43. The escape velocity from the Moon is much smaller than from Earth and is only 2.38 km/s. At what temperature would hydrogen molecules (molecular mass is equal to 2.016 g/mol) have an average velocity [latex]{v}_{\text{rms}}[/latex] equal to the Moon’s escape velocity?
44. Nuclear fusion, the energy source of the Sun, hydrogen bombs, and fusion reactors, occurs much more readily when the average kinetic energy of the atoms is high—that is, at high temperatures. Suppose you want the atoms in your fusion experiment to have average kinetic energies of [latex]6\text{.}\text{40}×{\text{10}}^{–\text{14}}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex]. What temperature is needed?
45. Suppose that the average velocity [latex]\left({v}_{\text{rms}}\right)[/latex] of carbon dioxide molecules (molecular mass is equal to 44.0 g/mol) in a flame is found to be [latex]1\text{.}\text{05}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex]. What temperature does this represent?
46. Hydrogen molecules (molecular mass is equal to 2.016 g/mol) have an average velocity [latex]{v}_{\text{rms}}[/latex] equal to 193 m/s. What is the temperature?
47. Much of the gas near the Sun is atomic hydrogen. Its temperature would have to be [latex]1\text{.}5×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{K}[/latex] for the average velocity [latex]{v}_{\text{rms}}[/latex] to equal the escape velocity from the Sun. What is that velocity?
48. There are two important isotopes of uranium— [latex]{}^{\text{235}}\text{U}[/latex] and [latex]{}^{\text{238}}\text{U}[/latex]; these isotopes are nearly identical chemically but have different atomic masses. Only [latex]{}^{\text{235}}\text{U}[/latex] is very useful in nuclear reactors. One of the techniques for separating them (gas diffusion) is based on the different average velocities [latex]{v}_{\text{rms}}[/latex] of uranium hexafluoride gas, [latex]{\text{UF}}_{6}[/latex]. (a) The molecular masses for [latex]{}^{\text{235}}\text{U}\phantom{\rule{0.25em}{0ex}}[/latex][latex]{\text{UF}}_{6}[/latex] and [latex]{}^{\text{238}}\text{U}[/latex][latex]\phantom{\rule{0.25em}{0ex}}{\text{UF}}_{6}[/latex] are 349.0 g/mol and 352.0 g/mol, respectively. What is the ratio of their average velocities? (b) At what temperature would their average velocities differ by 1.00 m/s? (c) Do your answers in this problem imply that this technique may be difficult?

Glossary

thermal energy

[latex]\overline{\text{KE}}[/latex], the average translational kinetic energy of a molecule