"

Fluid Dynamics and Its Biological and Medical Applications

88 Viscosity and Laminar Flow; Poiseuille’s Law

Learning Objectives

Laminar Flow and Viscosity

When you pour water or juice, it flows quickly and easily. But when you pour syrup or honey, the flow is slower and the fluid resists motion. This resistance to flow is due to a property called viscosity. Low-viscosity fluids, like water, flow easily, while high-viscosity fluids, like syrup or blood, resist motion more significantly. In this section, we examine how viscosity and flow characteristics affect fluid motion, particularly in biological systems.

To understand viscosity quantitatively, we first need to distinguish between two types of fluid flow: laminar flow and turbulent flow.

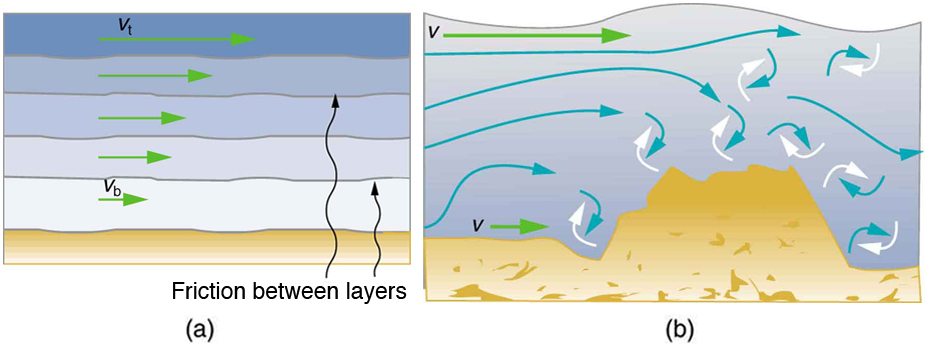
In laminar flow, fluid moves in smooth, parallel layers with no mixing between them. In contrast, turbulent flow features chaotic eddies and swirls where layers mix and the direction of motion becomes irregular. These behaviors are illustrated in Figure 88.1 , which shows smoke transitioning from smooth, orderly laminar flow into disordered turbulence.

Photograph of smoke rising smoothly for a while and then beginning to form swirls and eddies.
Figure 88.1 Smoke initially exhibits laminar flow, then transitions into turbulence with swirls and eddies. Laminar flow allows faster, more orderly movement; turbulence increases resistance. (credit: Creativity103)

The difference between these two types of flow is further clarified in Figure 88.2, where laminar flow is depicted as distinct layers gliding smoothly, while turbulent flow involves irregular, multi-directional motion due to obstructions or high speeds.

Part a of the figure shows a laminar flow on a fixed smooth surface. The different layers of the liquid are shown as different colored bands along the horizontal surface. The friction is shown to act all along the line separating two layers. The direction of flow of the fluid is toward right and the velocity is shown as v b for layers at the bottom and v t for layers on top. Part b of the figure shows turbulent flow on a surface with some obstruction. The fluid directions are horizontal on smooth path and irregular near the area of the obstruction. The velocity is v on top as well as at the bottom of the fluid.
Figure 88.2 (a) Laminar flow: fluid flows in parallel layers with smooth velocity profiles. (b) Turbulent flow: eddies and irregular motion occur due to obstructions or high velocity.

In experimental setups, such as the one shown in Figure 88.3, viscosity is measured by observing how much force is needed to drag a layer of fluid between two plates. The top plate moves at a velocity [latex]v[/latex], while the bottom plate is stationary. The fluid’s velocity varies linearly from 0 at the bottom to [latex]v[/latex] at the top, indicating a shear deformation.

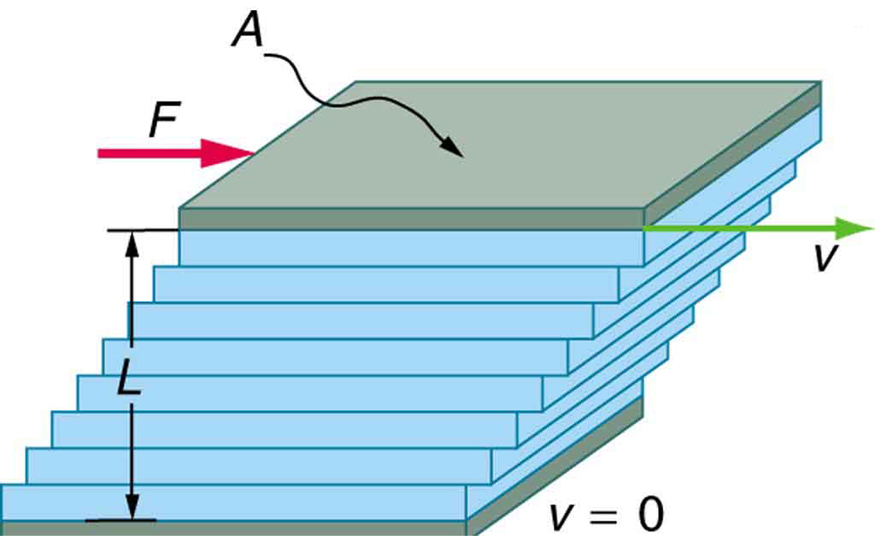
The figure shows the laminar flow of fluid between two rectangular plates each of area A. The bottom plate is shown as fixed. The distance between the plates is L. The top plate is shown to be pushed to right with a force F. The direction of movement of the layer of fluid in contact with the top plate is also toward right with velocity v. The fluid in contact with the plate in the bottom is shown to be in rest with v equals zero. As we see through the layers above the one on the bottom plate, each show a small displacement toward right in increasing order of value with the topmost layer showing the maximum.
Figure 88.3 Viscosity measured via laminar flow between two plates: the force [latex]F[/latex] required to maintain the top plate’s motion is related to the viscosity of the fluid.

Experiments show that the force [latex]F[/latex] required to maintain constant motion depends on:

The velocity [latex]v[/latex] of the top plate

The surface area [latex]A[/latex] of contact

The distance [latex]L[/latex] between plates

The viscosity [latex]\eta[/latex] of the fluid

These relationships combine to give:

[latex]F = \eta \frac{vA}{L}[/latex]

Solving for viscosity:

[latex]\eta = \frac{FL}{vA}[/latex]

Viscosity is measured in units of pascal-seconds (Pa·s). Substances like blood, mucus, and synovial fluid all exhibit different viscosities, which can vary with temperature and composition. In medicine, manipulating blood viscosity with drugs like aspirin is an important part of treating cardiovascular diseases.

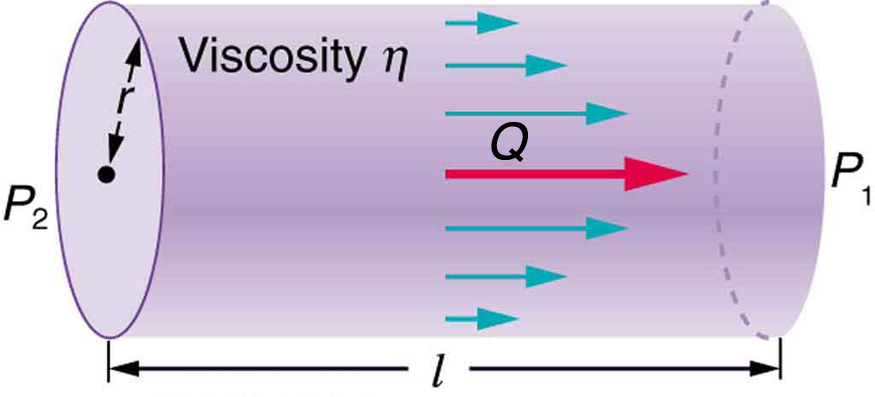
Flow Through Tubes and Poiseuille’s Law

Fluids flow in response to a pressure difference. If two points in a tube have different pressures, fluid will flow from high pressure to low pressure. This relationship is described by:

[latex]Q = \frac{P_2 - P_1}{R}[/latex]

Where:

[latex]Q[/latex] is the flow rate

[latex]P_1[/latex] and [latex]P_2[/latex] are the pressures at two locations

[latex]R[/latex] is the resistance to flow

Resistance depends on many factors. It increases with fluid viscosity and tube length, and decreases dramatically with increasing radius. For laminar flow through a cylindrical tube, the resistance is described by Poiseuille’s law:

[latex]R = \frac{8 \eta l}{\pi r^4}[/latex]

This equation shows that resistance is:

Directly proportional to fluid viscosity [latex]\eta[/latex]

Directly proportional to tube length [latex]l[/latex]

Inversely proportional to the fourth power of tube radius [latex]r[/latex]

This last point is especially important in biological systems. For instance, a small decrease in artery radius (due to plaque buildup) leads to a large increase in resistance and thus a decrease in blood flow. This sensitivity is critical in understanding conditions like hypertension.

We can combine the expressions for flow rate and resistance into a single formula for flow in laminar conditions:

[latex]Q = \frac{(P_2 - P_1)\pi r^4}{8 \eta l}[/latex]

This is the full form of Poiseuille’s Law for laminar flow. It accurately describes fluid flow in small-diameter vessels such as capillaries and arterioles—an essential concept in physiology and biomedical engineering.

Part a of the diagram shows a fluid flow across a rectangular non viscous medium. The speed of the fluid is shown to be same across the tube represented as same length of vertical rising arrows. Part b of the diagram shows a fluid flow across a rectangular viscous medium. The speed of the fluid speed at the walls is zero, increasing steadily to its maximum at the center of the tube represented as wave like variation for length of vertical rising arrows. Part c of the figure shows a burning Bunsen burner.
Figure 88.4 (a) In ideal (non-viscous) flow, velocity is uniform across the tube. (b) In viscous flow, velocity is highest in the center and zero at the walls. (c) A Bunsen burner flame visualizes this velocity gradient. (credit: Jason Woodhead)

Example 88.1 Using Flow Rate: Plaque Deposits Reduce Blood Flow

Suppose the flow rate of blood in a coronary artery has been reduced to half its normal value by plaque deposits. By what factor has the radius of the artery been reduced, assuming no turbulence occurs?

Strategy

Assuming laminar flow, Poiseuille’s law states that

[latex]Q=\frac{\left({P}_{2}-{P}_{1}\right){\mathrm{\pi r}}^{4}}{8\eta l}\text{.}[/latex]

We need to compare the artery radius before and after the flow rate reduction.

Solution

With a constant pressure difference assumed and the same length and viscosity, along the artery we have

[latex]\frac{{Q}_{1}}{{r}_{1}^{4}}=\frac{{Q}_{2}}{{r}_{2}^{4}}\text{.}[/latex]

So, given that [latex]{Q}_{2}=0\text{.}\text{5}{Q}_{1}[/latex], we find that [latex]{r}_{2}^{4}=0\text{.}{5r}_{1}^{4}[/latex].

Therefore, [latex]{r}_{2}={\left(0\text{.}5\right)}^{0\text{.}\text{25}}{r}_{1}=0\text{.}\text{841}{r}_{1}[/latex], a decrease in the artery radius of 16%.

Discussion

This decrease in radius is surprisingly small for this situation. To restore the blood flow in spite of this buildup would require an increase in the pressure difference [latex]\left({P}_{2}-{P}_{1}\right)[/latex] of a factor of two, with subsequent strain on the heart.

Table 88.1 Coefficients of Viscosity of Various Fluids
Fluid Temperature (ºC) Viscosity
[latex]\eta \phantom{\rule{0.25em}{0ex}}\text{(mPa·s)}[/latex]
Gases
Air 0 0.0171
20 0.0181
40 0.0190
100 0.0218
Ammonia 20 0.00974
Carbon dioxide 20 0.0147
Helium 20 0.0196
Hydrogen 0 0.0090
Mercury 20 0.0450
Oxygen 20 0.0203
Steam 100 0.0130
Liquids
Water 0 1.792
20 1.002
37 0.6947
40 0.653
100 0.282
Whole blood1 20 3.015
37 2.084
Blood plasma2 20 1.810
37 1.257
Ethyl alcohol 20 1.20
Methanol 20 0.584
Oil (heavy machine) 20 660
Oil (motor, SAE 10) 30 200
Oil (olive) 20 138
Glycerin 20 1500
Honey 20 2000–10000
Maple Syrup 20 2000–3000
Milk 20 3.0
Oil (Corn) 20 65

Applications of Poiseuille’s Law in the Circulatory System

The circulatory system provides an excellent biological context for understanding Poiseuille’s law. Blood flow through arteries, arterioles, and capillaries behaves in many ways like fluid flow in tubes. Importantly, the blood vessels are not rigid—they are elastic and can change diameter to regulate blood distribution throughout the body.

According to Poiseuille’s law, flow rate [latex]Q[/latex] is extremely sensitive to changes in the radius of a vessel, since radius appears to the fourth power in the denominator of the resistance formula. Small changes in radius can result in large changes in flow. This principle is used by the body to control circulation. During intense physical activity, blood vessels leading to muscles dilate (widen), dramatically increasing flow to those tissues. Simultaneously, other vessels may constrict to redirect blood to where it is most needed.

Conversely, conditions such as atherosclerosis can reduce vessel radius due to plaque buildup, significantly decreasing blood flow. For example, if a vessel’s radius is reduced by just 5%, becoming 0.95 of its original size, the new flow rate becomes:

[latex](0.95)^4 = 0.81[/latex]

This means the flow rate drops to 81% of its original value—a 19% decrease—despite only a small narrowing of the vessel. To compensate, the body may raise blood pressure by a similar amount. However, chronically increased pressure poses health risks, including increased strain on the heart and the possibility of rupturing weakened vessel walls.

This principle is also relevant outside biology. For example, in automobile engines, motor oil has higher viscosity when cold, making it harder to pump. That’s why oil pressure is often higher during engine startup—greater pressure is required to maintain flow until the oil warms up and thins.

The figure shows a section of a cylindrical tube of length l. The two end cross section are shown to have pressure P two and P one respectively. The radius of the cylindrical tube is given by r. The direction of flow is shown by horizontal arrows toward right end of the tube. The flow rate is marked as Q.
Figure 88.5 Poiseuille’s law describes flow through a cylindrical tube of radius [latex]r[/latex], length [latex]l[/latex], and viscosity [latex]\eta[/latex]. Flow occurs from high pressure [latex]P_2[/latex] to low pressure [latex]P_1[/latex], and flow rate [latex]Q[/latex] is directly proportional to the pressure difference and [latex]r^4[/latex], but inversely proportional to viscosity and length.

Example 88.2 What Pressure Produces This Flow Rate?

An intravenous (IV) system is supplying saline solution to a patient at the rate of [latex]0\text{.}\text{120}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}\text{/s}[/latex] through a needle of radius 0.150 mm and length 2.50 cm. What pressure is needed at the entrance of the needle to cause this flow, assuming the viscosity of the saline solution to be the same as that of water? The gauge pressure of the blood in the patient’s vein is 8.00 mm Hg. (Assume that the temperature is
[latex]\text{20ºC}[/latex]
.)

Strategy

Assuming laminar flow, Poiseuille’s law applies. This is given by

[latex]Q=\frac{\left({P}_{2}-{P}_{1}\right)\pi {r}^{4}}{8\eta l}\text{,}[/latex]

where [latex]{P}_{2}[/latex] is the pressure at the entrance of the needle and [latex]{P}_{1}[/latex] is the pressure in the vein. The only unknown is [latex]{P}_{2}[/latex].

Solution

Solving for [latex]{P}_{2}[/latex] yields

[latex]{P}_{2}=\frac{8\eta l}{{\mathrm{\pi r}}^{4}}Q+{P}_{1\text{.}}[/latex]

[latex]{P}_{1}[/latex] is given as 8.00 mm Hg, which converts to [latex]1\text{.}\text{066}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. Substituting this and the other known values yields

[latex]\begin{array}{lll}{P}_{2}& =& [\frac{8(1\text{.}\text{00}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{N}\cdot {\text{s/m}}^{2})(2\text{.}\text{50}×{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}\text{m})}{\pi (0\text{.}\text{150}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{m}{)}^{4}}](1\text{.}\text{20}×{\text{10}}^{-7}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{3}\text{/s})+1\text{.}\text{066}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\\ & =& 1\text{.}\text{62}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}\text{.}\end{array}[/latex]

Discussion

This pressure could be supplied by an IV bottle with the surface of the saline solution 1.61 m above the entrance to the needle (this is left for you to solve in this chapter’s Problems and Exercises), assuming that there is negligible pressure drop in the tubing leading to the needle.

Flow, Resistance, and Pressure Drops

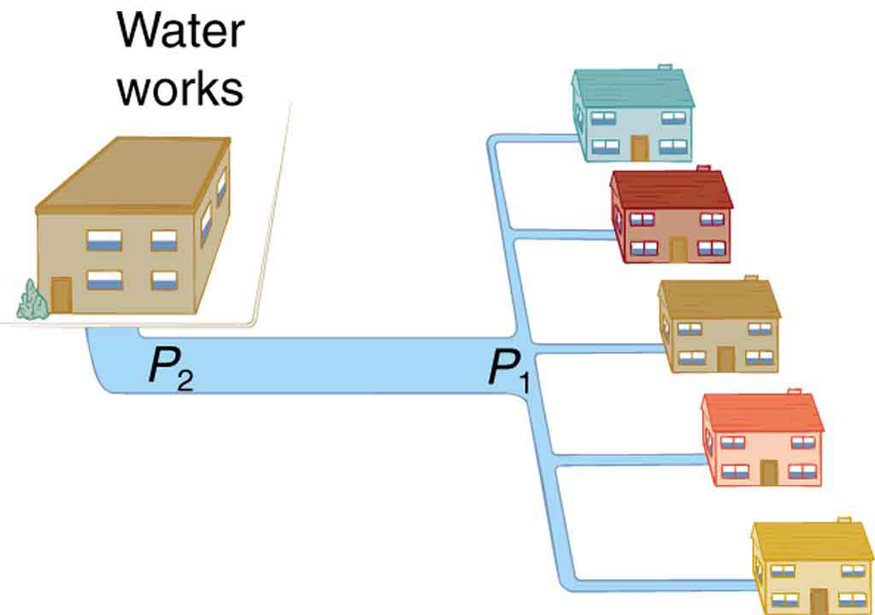
Have you ever noticed a drop in water pressure at home during peak usage times, such as on hot summer days (see Figure 88.6)? This pressure decrease is due to increased water usage in your neighborhood, which causes a pressure drop in the main water supply line. The same principle applies to biological systems like the circulatory system, where pressure drops occur due to resistance in blood vessels.

To understand this, consider the equation for flow rate:

[latex]Q = \frac{{P}_{2} - {P}_{1}}{R}[/latex]

Rearranging gives the pressure drop across a system:

[latex]{P}_{2} - {P}_{1} = RQ[/latex]

In this context, [latex]{P}{2}[/latex] is the pressure at the waterworks or the heart, [latex]{P}{1}[/latex] is the pressure at the endpoint (such as your faucet or capillaries), and [latex]R[/latex] is the resistance of the pipe or vessel. A high flow rate [latex]Q[/latex] increases the pressure drop [latex]{P}{2} - {P}{1}[/latex], meaning that the pressure at the endpoint ([latex]{P}_{1}[/latex]) decreases during heavy use.

Figure shows the water distribution system from a water works to homes around that area. The pressure at the pipeline near the water works is shown to have a pressure P two and the pressure at the dividing point were the pipe line splits to corresponding houses the pressure is shown as P one.
Figure 88.6 During times of heavy use, pressure at the end of a pipeline ([latex]{P}_{1}[/latex]) drops significantly compared to the source pressure ([latex]{P}_{2}[/latex]) due to resistance. If the flow is minimal, the pressure drop is negligible and [latex]{P}_{2} \approx {P}_{1}[/latex].

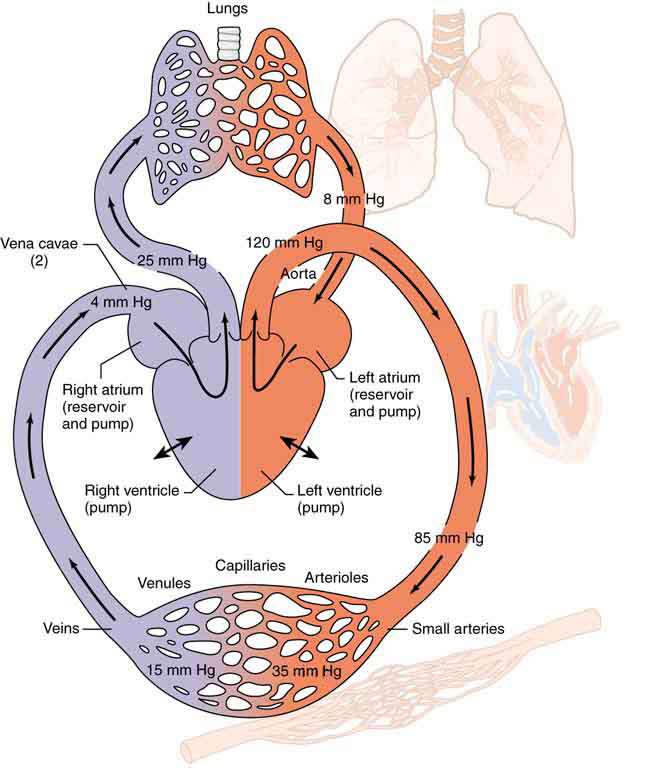
This same principle explains pressure changes in the circulatory system (Figure 88.7). If blood encounters narrowed or obstructed arteries—such as those affected by plaque—[latex]R[/latex] increases dramatically. For a given [latex]Q[/latex], this leads to a large pressure drop, resulting in reduced pressure and flow beyond the obstruction. Furthermore, if the narrowing causes turbulence, the resistance increases even more.

Figure is a schematic diagram of the circulatory system. The lungs, heart, arteries and vein systems are shown. The blood is shown to flow from the left atrium through the arteries, then through the veins and back to the right atrium. The flow is also shown from right atrium to the lungs and from lungs back to left atrium. All parts of the system are labeled. Pressure various points of the system all along the movement of blood across various parts are also marked.
Figure 88.7 Schematic of the human circulatory system. Pressure is generated by the heart’s two pumps and decreases as blood flows through vessels due to resistance. Blood pressure and flow can be regulated by changing vessel diameter, allowing flexible blood distribution to organs.

Branching in the circulatory system reduces resistance by increasing the total cross-sectional area. For instance, a single artery with a cross-sectional area of [latex]1\ \text{cm}^2[/latex] might branch into 20 smaller arteries with cross-sectional areas of [latex]0.5\ \text{cm}^2[/latex] each, totaling [latex]10\ \text{cm}^2[/latex]. This lowers resistance and helps maintain pressure further downstream.

Since flow rate is related to velocity and cross-sectional area by

[latex]Q = A \bar{v}[/latex]

increased area due to branching means that average velocity [latex]\bar{v}[/latex] decreases. For example, blood travels through the aorta (diameter ~1 cm) at about 25 cm/s, but slows down to around 1 mm/s in the capillaries (diameter ~20 μm). This slow speed is vital for enabling exchange of oxygen, nutrients, and waste products at the cellular level.

Section Summary

  • Laminar flow: Smooth, layered motion of fluid without mixing.
  • Turbulent flow: Chaotic flow with eddies and swirls that increase resistance.
  • Viscosity [latex]\eta[/latex]: Internal fluid friction; unit is [latex]\text{Pa}\cdot\text{s}[/latex].
  • Flow rate:
    [latex]Q = \frac{{P}_{2} - {P}_{1}}{R}[/latex]
  • Poiseuille’s law for resistance:
    [latex]R = \frac{8\eta l}{\pi r^4}[/latex]
  • Poiseuille’s law for flow rate:
    [latex]Q = \frac{(P_2 - P_1)\pi r^4}{8\eta l}[/latex]
  • Pressure drop:
    [latex]{P}_{2} - {P}_{1} = RQ[/latex]

Conceptual Questions

  1. Explain why the viscosity of a liquid decreases with temperature—that is, how might increased temperature reduce the effects of cohesive forces in a liquid? Also explain why the viscosity of a gas increases with temperature—that is, how does increased gas temperature create more collisions between atoms and molecules?
  2. When paddling a canoe upstream, it is wisest to travel as near to the shore as possible. When canoeing downstream, it may be best to stay near the middle. Explain why.
  3. Why does flow decrease in your shower when someone flushes the toilet?
  4. Plumbing usually includes air-filled tubes near water faucets, as shown in Figure 88.8. Explain why they are needed and how they work.
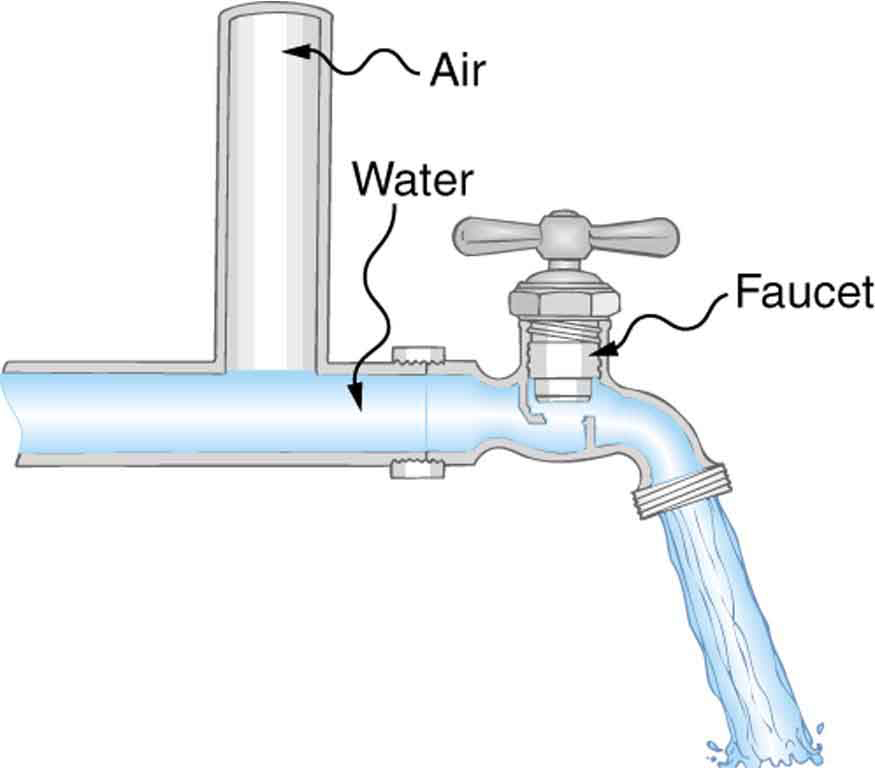
    The picture shows water gushing out of a water tap. The faucet in the tap is marked. A pipe connected vertically filled with air is shown at an opening on the water pipe before the tap.
    Figure 88.8 The vertical tube near the water tap remains full of air and serves a useful purpose.

Problems & Exercises

  1. (a) Calculate the retarding force due to the viscosity of the air layer between a cart and a level air track given the following information—air temperature is [latex]\text{20º C}[/latex], the cart is moving at 0.400 m/s, its surface area is [latex]2\text{.}\text{50}×{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex], and the thickness of the air layer is [latex]6.00×{\text{10}}^{-5}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. (b) What is the ratio of this force to the weight of the 0.300-kg cart?
  2. What force is needed to pull one microscope slide over another at a speed of 1.00 cm/s, if there is a 0.500-mm-thick layer of [latex]\text{20º C}[/latex] water between them and the contact area is [latex]8.00\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]?
  3. A glucose solution being administered with an IV has a flow rate of [latex]4\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}\text{/min}[/latex]. What will the new flow rate be if the glucose is replaced by whole blood having the same density but a viscosity 2.50 times that of the glucose? All other factors remain constant.
  4. The pressure drop along a length of artery is 100 Pa, the radius is 10 mm, and the flow is laminar. The average speed of the blood is 15 mm/s. (a) What is the net force on the blood in this section of artery? (b) What is the power expended maintaining the flow?
  5. A small artery has a length of [latex]1\text{.}1×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] and a radius of [latex]2.5×{\text{10}}^{-5}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. If the pressure drop across the artery is 1.3 kPa, what is the flow rate through the artery? (Assume that the temperature is [latex]\text{37º C}[/latex].)
  6. Fluid originally flows through a tube at a rate of [latex]\text{100}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{3}\text{/s}[/latex]. To illustrate the sensitivity of flow rate to various factors, calculate the new flow rate for the following changes with all other factors remaining the same as in the original conditions. (a) Pressure difference increases by a factor of 1.50. (b) A new fluid with 3.00 times greater viscosity is substituted. (c) The tube is replaced by one having 4.00 times the length. (d) Another tube is used with a radius 0.100 times the original. (e) Yet another tube is substituted with a radius 0.100 times the original and half the length, and the pressure difference is increased by a factor of 1.50.
  7. The arterioles (small arteries) leading to an organ, constrict in order to decrease flow to the organ. To shut down an organ, blood flow is reduced naturally to 1.00% of its original value. By what factor did the radii of the arterioles constrict? Penguins do this when they stand on ice to reduce the blood flow to their feet.
  8. Angioplasty is a technique in which arteries partially blocked with plaque are dilated to increase blood flow. By what factor must the radius of an artery be increased in order to increase blood flow by a factor of 10?
  9. (a) Suppose a blood vessel’s radius is decreased to 90.0% of its original value by plaque deposits and the body compensates by increasing the pressure difference along the vessel to keep the flow rate constant. By what factor must the pressure difference increase? (b) If turbulence is created by the obstruction, what additional effect would it have on the flow rate?
  10. A spherical particle falling at a terminal speed in a liquid must have the gravitational force balanced by the drag force and the buoyant force. The buoyant force is equal to the weight of the displaced fluid, while the drag force is assumed to be given by Stokes Law, [latex]{F}_{s}=\text{6}\pi r\eta v[/latex]. Show that the terminal speed is given by [latex]v=\frac{{2R}^{2}g}{9\eta }\left({\rho }_{\text{s}}-{\rho }_{1}\right),[/latex] where [latex]R[/latex] is the radius of the sphere, [latex]{\rho }_{\text{s}}[/latex] is its density, and [latex]{\rho }_{1}[/latex] is the density of the fluid and [latex]\eta[/latex] the coefficient of viscosity.
  11. Using the equation of the previous problem, find the viscosity of motor oil in which a steel ball of radius 0.8 mm falls with a terminal speed of 4.32 cm/s. The densities of the ball and the oil are 7.86 and 0.88 g/mL, respectively.
  12. A skydiver will reach a terminal velocity when the air drag equals their weight. For a skydiver with high speed and a large body, turbulence is a factor. The drag force then is approximately proportional to the square of the velocity. Taking the drag force to be [latex]{F}_{\text{D}}=\frac{1}{2}\rho {\mathrm{Av}}^{\text{2}}[/latex] and setting this equal to the person’s weight, find the terminal speed for a person falling “spread eagle.” Find both a formula and a number for [latex]{v}_{\text{t}}[/latex], with assumptions as to size.
  13. A layer of oil 1.50 mm thick is placed between two microscope slides. Researchers find that a force of [latex]5\text{.}\text{50}×{\text{10}}^{-4}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex] is required to glide one over the other at a speed of 1.00 cm/s when their contact area is [latex]6\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex]. What is the oil’s viscosity? What type of oil might it be?
  14. (a) Verify that a 19.0% decrease in laminar flow through a tube is caused by a 5.00% decrease in radius, assuming that all other factors remain constant, as stated in the text. (b) What increase in flow is obtained from a 5.00% increase in radius, again assuming all other factors remain constant?
  15. Example 88.2 dealt with the flow of saline solution in an IV system. (a) Verify that a pressure of [latex]1\text{.}\text{62}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] is created at a depth of 1.61 m in a saline solution, assuming its density to be that of sea water. (b) Calculate the new flow rate if the height of the saline solution is decreased to 1.50 m. (c) At what height would the direction of flow be reversed? (This reversal can be a problem when patients stand up.)
  16. When physicians diagnose arterial blockages, they quote the reduction in flow rate. If the flow rate in an artery has been reduced to 10.0% of its normal value by a blood clot and the average pressure difference has increased by 20.0%, by what factor has the clot reduced the radius of the artery?
  17. During a marathon race, a runner’s blood flow increases to 10.0 times her resting rate. Her blood’s viscosity has dropped to 95.0% of its normal value, and the blood pressure difference across the circulatory system has increased by 50.0%. By what factor has the average radii of her blood vessels increased?
  18. Water supplied to a house by a water main has a pressure of [latex]3\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex] early on a summer day when neighborhood use is low. This pressure produces a flow of 20.0 L/min through a garden hose. Later in the day, pressure at the exit of the water main and entrance to the house drops, and a flow of only 8.00 L/min is obtained through the same hose. (a) What pressure is now being supplied to the house, assuming resistance is constant? (b) By what factor did the flow rate in the water main increase in order to cause this decrease in delivered pressure? The pressure at the entrance of the water main is [latex]5\text{.}\text{00}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex], and the original flow rate was 200 L/min. (c) How many more users are there, assuming each would consume 20.0 L/min in the morning?
  19. An oil gusher shoots crude oil 25.0 m into the air through a pipe with a 0.100-m diameter. Neglecting air resistance but not the resistance of the pipe, and assuming laminar flow, calculate the gauge pressure at the entrance of the 50.0-m-long vertical pipe. Take the density of the oil to be [latex]\text{900}\phantom{\rule{0.25em}{0ex}}{\text{kg/m}}^{3}[/latex] and its viscosity to be [latex]1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\left({\text{N/m}}^{2}\right)\cdot \text{s}[/latex] (or [latex]1.00\phantom{\rule{0.25em}{0ex}}\text{Pa}\cdot \text{s}[/latex]). Note that you must take into account the pressure due to the 50.0-m column of oil in the pipe.
  20. Concrete is pumped from a cement mixer to the place it is being laid, instead of being carried in wheelbarrows. The flow rate is 200.0 L/min through a 50.0-m-long, 8.00-cm-diameter hose, and the pressure at the pump is [latex]8\text{.}\text{00}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. (a) Calculate the resistance of the hose. (b) What is the viscosity of the concrete, assuming the flow is laminar? (c) How much power is being supplied, assuming the point of use is at the same level as the pump? You may neglect the power supplied to increase the concrete’s velocity.
  21. Construct Your Own Problem Consider a coronary artery constricted by arteriosclerosis. Construct a problem in which you calculate the amount by which the diameter of the artery is decreased, based on an assessment of the decrease in flow rate.
  22. Consider a river that spreads out in a delta region on its way to the sea. Construct a problem in which you calculate the average speed at which water moves in the delta region, based on the speed at which it was moving up river. Among the things to consider are the size and flow rate of the river before it spreads out and its size once it has spread out. You can construct the problem for the river spreading out into one large river or into multiple smaller rivers.

Footnotes

  1. 1 The ratios of the viscosities of blood to water are nearly constant between 0°C and 37°C.
  2. 2 See note on Whole Blood.

Glossary

laminar
a type of fluid flow in which layers do not mix
turbulence
fluid flow in which layers mix together via eddies and swirls
viscosity
the friction in a fluid, defined in terms of the friction between layers
Poiseuille’s law for resistance
the resistance to laminar flow of an incompressible fluid in a tube: R = 8ηl/πr4
Poiseuille’s law
the rate of laminar flow of an incompressible fluid in a tube: Q = (P2 − P1)πr4/8ηl
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book