Statics and Torque
65 Forces and Torques in Muscles and Joints
Learning Objectives
- Explain the forces exerted by muscles.
- State how a bad posture causes back strain.
- Discuss the benefits of skeletal muscles attached close to joints.
- Discuss various complexities in the real system of muscles, bones, and joints.
The study of the biomechanics of muscles and bones reveals how our bodies operate like complex simple machines. The forces within the body can be surprisingly large, often much greater than the external loads we handle. This is due to the geometry of skeletal muscles and how they attach to the bones via tendons close to joints. While this arrangement allows for quick and precise movement, it also means that the mechanical advantage of these systems is less than 1, requiring high internal forces from muscles.
Consider the human arm as illustrated in Figure 65.1. The biceps apply an upward force [latex]{F}_{\text{B}}[/latex] to hold a book stationary in the hand. This force must balance not only the downward force from the weight of the book but also the weight of the arm itself. Since the biceps tendon is attached very close to the elbow joint, the lever arm for [latex]{F}_{\text{B}}[/latex] is much shorter than that for the book’s weight, leading to a low mechanical advantage.
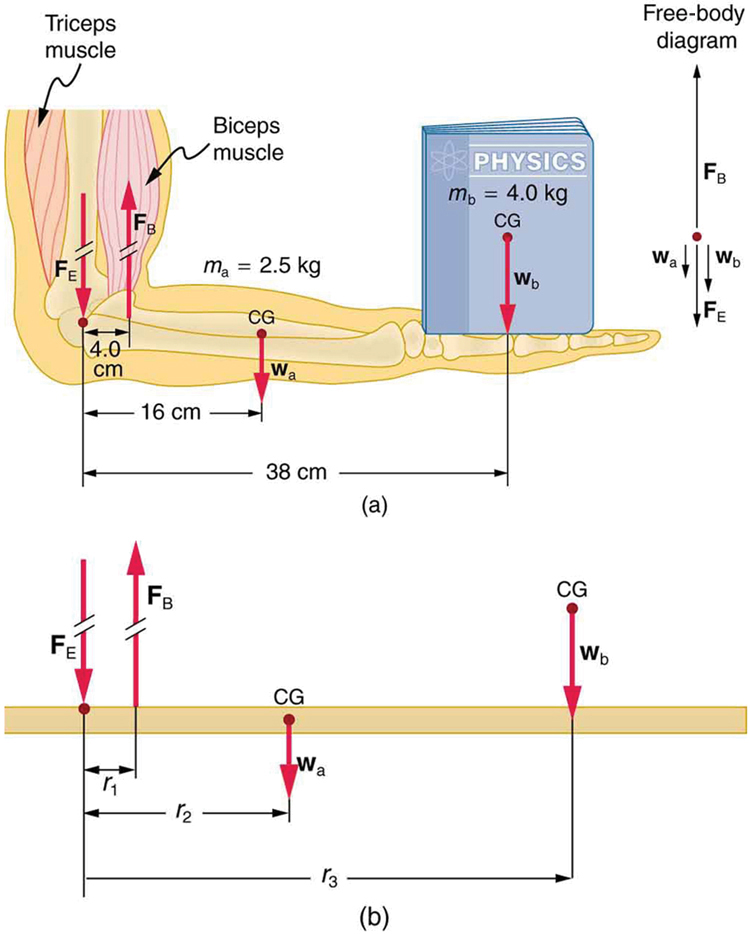
Let’s analyze the torques in this system to understand how much force the biceps must apply. Assume the arm is horizontal and stationary, meaning the net torque about the elbow (pivot) is zero:
Here:
- [latex]r_1[/latex] is the distance from the elbow to the point of biceps attachment,
- [latex]r_2[/latex] is the distance to the center of gravity of the arm,
- [latex]r_3[/latex] is the distance to the center of gravity of the book,
- [latex]w_{\text{arm}}[/latex] is the weight of the arm, and
- [latex]w_{\text{book}}[/latex] is the weight of the book.
Solving this equation gives us the required force from the biceps to keep the system in static equilibrium. Because [latex]r_1[/latex] is small, [latex]F_B[/latex] must be large to balance the torques created by the larger weights at longer lever arms. This explains why muscles generate forces far exceeding the loads they hold.
This arrangement, while inefficient in terms of force, is highly effective for fast and precise control of limb movement. Attaching muscles near joints minimizes the angular moment of inertia, making limbs easier to rotate rapidly—an evolutionary advantage for reflexive or coordinated motion.
Posture and Back Strain
Improper posture can create large torques in the back due to increased horizontal distances between the center of gravity and the spinal pivot. For example, when bending over with a load, the torque due to the load and the upper body weight increases dramatically if the load is held far from the spine. The back muscles must then exert very large forces to maintain equilibrium, which can lead to fatigue or injury.
To reduce back strain, it is essential to keep the load close to the body, reduce the total load, and bend the knees rather than the back, which allows the legs to support more of the weight.
Example 65.1: Muscles Exert Bigger Forces Than You Might Think
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in Figure 65.1, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is [latex]{F}_{\text{B}}[/latex]; that of the elbow joint is [latex]{F}_{\text{E}}[/latex]; that of the weights of the forearm is [latex]{w}_{\text{a}}[/latex], and its load is [latex]{w}_{\text{b}}[/latex]. Two of these are unknown ([latex]{F}_{\text{B}}[/latex] and [latex]{F}_{\text{E}}[/latex]), so that the first condition for equilibrium cannot by itself yield [latex]{F}_{\text{B}}[/latex]. But if we use the second condition and choose the pivot to be at the elbow, then the torque due to [latex]{F}_{\text{E}}[/latex] is zero, and the only unknown becomes [latex]{F}_{\text{B}}[/latex].
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium [latex]\left(\text{net}\phantom{\rule{0.25em}{0ex}}\tau =\text{0}\right)[/latex] becomes
Note that [latex]\text{sin}\phantom{\rule{0.25em}{0ex}}\theta =1[/latex] for all forces, since [latex]\theta =\text{90º}[/latex] for all forces. This equation can easily be solved for [latex]{F}_{\text{B}}[/latex] in terms of known quantities, yielding
Entering the known values gives
which yields
Now, the combined weight of the arm and its load is [latex]\left(\text{6.50 kg}\right)\left(\text{9.80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right)=\text{63.7 N}[/latex], so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
The force a muscle can exert depends on its length and the angle of the limb. In the case of the biceps, as the forearm angle changes from 90°, the muscle shortens, reducing its capacity to generate force. This biomechanical limitation is due to the length–tension relationship in muscle fibers—muscles produce the most force when slightly stretched beyond their resting length.
Joint forces can also be surprisingly large. In the earlier example, the elbow joint experiences a downward force [latex]{F}_{\text{E}}[/latex] of about 407 N, which is over six times greater than the weight supported. This happens because the upward force by the muscle must counter not only the load’s torque but also its own geometry-induced mechanical disadvantage. For equilibrium:
These force magnitudes explain why injuries can occur even during seemingly light tasks, especially when the load is located far from the joint. Increasing the lever arm increases the torque required to maintain static equilibrium, thus increasing muscle force and joint stress.
Activities such as swinging a racquet or bat, particularly with poor technique or ill-fitted equipment, can cause excessive and repetitive torque on muscles and tendons. The phenomenon of “tennis elbow,” for instance, arises from repeated extension and torque applied to the elbow joint with low mechanical advantage. Proper grip, alignment, and targeting the racquet’s “sweet spot” can minimize the force transmitted through the arm and reduce injury risk.
Posture and Torque on the Spine
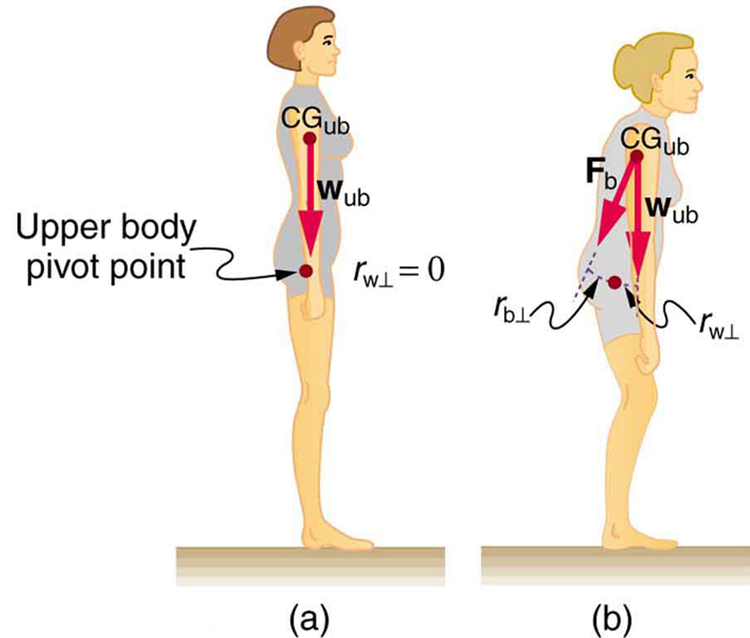
Figure 65.2 illustrates how posture affects torque on the hips and lower back. In part (a), good posture positions the upper body’s center of gravity (cg) directly above the pivot point at the hips, requiring only a vertical support force with minimal or no muscular effort. In this case, the torque about the pivot is zero:
However, in part (b), poor posture shifts the cg forward, creating a clockwise torque about the hips. This must be countered by large forces from the lower back muscles, which have a short perpendicular lever arm [latex]{r}_{\text{b} \perp}[/latex] relative to the cg’s moment arm. The required muscle force [latex]{F}_{\text{b}}[/latex] is therefore quite large:
Solving for the back muscle force gives:
Because [latex]r_{\text{cg}} \gg r_{\text{b} \perp}[/latex], the muscle force is much larger than the body’s weight. Prolonged muscle activity in this posture can lead to fatigue and back pain.
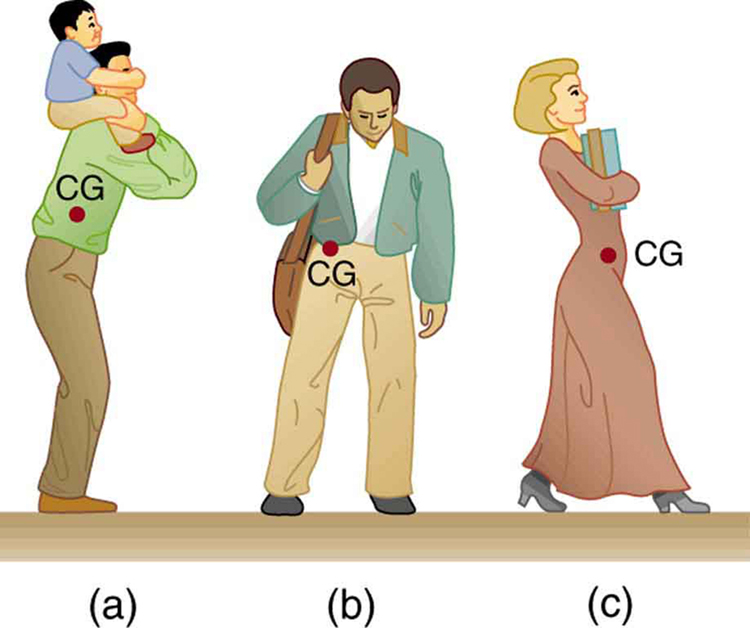
The rule of equilibrium requires that the overall center of gravity remain over the base of support (feet). When carrying loads, people instinctively adjust their posture to restore balance. This is shown in Figure 65.3, where a person leans forward with a child on their shoulders, leans sideways with a bag on one side, or leans backward when carrying books in the arms.
Takeaway on Lifting and Load Positioning
The torque on the spine and joints increases dramatically with poor load handling. Bending at the waist to lift something puts the load far from the back pivot point, increasing [latex]r[/latex] in the torque equation:
To reduce torque and associated muscle strain, always lift with your legs (reducing [latex]r[/latex]) and keep the object close to your body’s center of gravity.
Example 65.2: Do Not Lift with Your Back
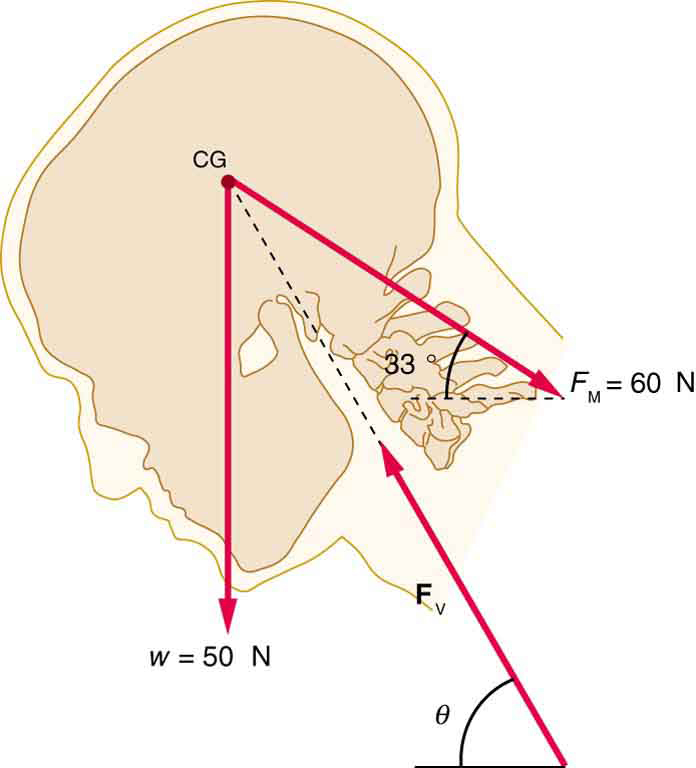
Consider the person lifting a heavy box with his back, shown in Figure 65.4. (a) Calculate the magnitude of the force [latex]{F}_{\text{B}}–[/latex] in the back muscles that is needed to support the upper body plus the box and compare this with his weight. The mass of the upper body is 55.0 kg and the mass of the box is 30.0 kg. (b) Calculate the magnitude and direction of the force [latex]{\mathbf{\text{F}}}_{\text{V}}–[/latex] exerted by the vertebrae on the spine at the indicated pivot point. Again, data in the figure may be taken to be accurate to three significant figures.
Strategy
By now, we sense that the second condition for equilibrium is a good place to start, and inspection of the known values confirms that it can be used to solve for [latex]{F}_{\text{B}}–[/latex] if the pivot is chosen to be at the hips. The torques created by [latex]{\mathbf{\text{w}}}_{\text{ub}}[/latex] and [latex]{\mathbf{\text{w}}}_{\text{box}}–[/latex] are clockwise, while that created by [latex]{\mathbf{\text{F}}}_{\text{B}}–[/latex] is counterclockwise.
Solution for (a)
Using the perpendicular lever arms given in the figure, the second condition for equilibrium [latex]\left(\text{net}\phantom{\rule{0.25em}{0ex}}\tau =\text{0}\right)[/latex] becomes
Solving for [latex]{F}_{\text{B}}[/latex] yields
The ratio of the force the back muscles exert to the weight of the upper body plus its load is
This force is considerably larger than it would be if the load were not present.
Solution for (b)
More important in terms of its damage potential is the force on the vertebrae [latex]{\mathbf{\text{F}}}_{\text{V}}[/latex]. The first condition for equilibrium ([latex]\text{net}\phantom{\rule{0.25em}{0ex}}\mathbf{\text{F}}=0[/latex]) can be used to find its magnitude and direction. Using [latex]y[/latex] for vertical and [latex]x[/latex] for horizontal, the condition for the net external forces along those axes to be zero
Starting with the vertical ([latex]y[/latex]) components, this yields
Thus,
yielding
Similarly, for the horizontal ([latex]x[/latex]) components,
yielding
The magnitude of [latex]{\mathbf{\text{F}}}_{\text{V}}[/latex] is given by the Pythagorean theorem:
The direction of [latex]{\mathbf{\text{F}}}_{\text{V}}[/latex] is
Note that the ratio of [latex]{F}_{\text{V}}[/latex] to the weight supported is
Discussion
This force is about 5.6 times greater than it would be if the person were standing erect. The trouble with the back is not so much that the forces are large—because similar forces are created in our hips, knees, and ankles—but that our spines are relatively weak. Proper lifting, performed with the back erect and using the legs to raise the body and load, creates much smaller forces in the back—in this case, about 5.6 times smaller.
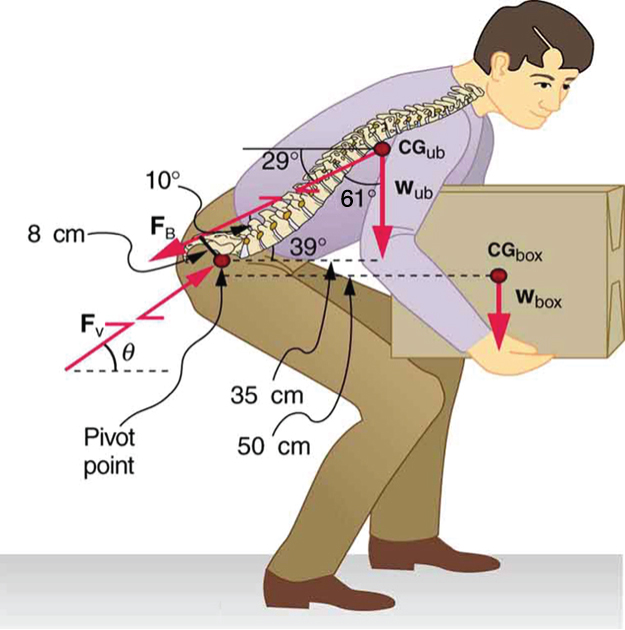
Lifting with the back, as shown in Figure 65.4, requires extremely large muscle forces because the perpendicular distance between the pivot point (hip joint) and the muscle force vector is very short. Meanwhile, the horizontal distance to the load (e.g., a box) is much longer, which results in a large torque that must be counteracted. This is why lifting with the back rather than the legs increases the risk of injury due to disc compression or muscle strain.
Advantages of Close Muscle Attachment
Why are skeletal muscles typically attached close to joints, even though this results in small mechanical advantages? The primary advantage is speed. Small contractions of muscles near the joints produce larger angular displacements at the limb ends, which enables fast motion. This arrangement also supports greater flexibility and agility, allowing vertebrates to perform a wide variety of coordinated actions.
For instance, if the biceps muscle were attached far from the elbow—say, at the wrist—it would lose both the mechanical control and fine-tuned movement range that vertebrates rely on. The trade-off for low mechanical advantage is thus improved control, speed, and maneuverability.
Complexities in Real Biological Systems
In practice, many joints behave more like dynamic systems than simple levers. As a joint flexes or extends, the pivot point often shifts, which causes both the perpendicular lever arms and the mechanical advantage to change continuously. This makes the required muscle force variable throughout the motion.
For example, the force the biceps must apply to support a weight changes as the angle of the forearm changes, because the torque equation:
depends on both the angle [latex]\theta[/latex] and the effective distance [latex]r[/latex] from the pivot point. This is also why seat height on a bicycle affects leg strain—if the leg angle isn’t optimal, muscle force and torque increase unnecessarily.
Despite these complexities, the basic statics principles described here provide a useful approximation for analyzing biological systems. When enough information is available about bone lengths, muscle positions, and joint mechanics, accurate predictions of forces and torques can be made. A deeper biomechanical model would also include muscle elasticity, tendon stiffness, and dynamic loading.
Many real-world injuries, like joint damage and muscle tears, are tied directly to the forces and torques we’ve examined. Strength training, physical therapy, and even ergonomic design rely heavily on these biomechanical principles to improve performance and reduce injury.
Section Summary
- Statics plays an important role in understanding the everyday forces and strains experienced by our muscles and bones.
- Many lever systems in the body operate with a mechanical advantage significantly less than one, since most skeletal muscles attach very close to joints.
- Good posture means standing or sitting so that the body’s center of gravity lies directly over the hip pivot point, which minimizes the torque on the back muscles and helps prevent strain or injury to spinal disks.
Conceptual Questions
- Why are the forces exerted on the outside world by the limbs of our bodies usually much smaller than the forces exerted by muscles inside the body?
- Explain why the forces in our joints are several times larger than the forces we exert on the outside world with our limbs. Can these forces be even greater than muscle forces?
- Certain types of dinosaurs were bipedal (walked on two legs). What is a good reason that these creatures invariably had long tails if they had long necks?
- Swimmers and athletes during competition need to go through certain postures at the beginning of the race. Consider the balance of the person and why start-offs are so important for races.
- If the maximum force the biceps muscle can exert is 1000 N, can we pick up an object that weighs 1000 N? Explain your answer.
- Suppose the biceps muscle was attached through tendons to the upper arm close to the elbow and the forearm near the wrist. What would be the advantages and disadvantages of this type of construction for the motion of the arm?
- Explain one of the reasons why pregnant women often suffer from back strain late in their pregnancy.
Problems & Exercises
- Verify that the force in the elbow joint in Example 65.1 is 407 N, as stated in the text.
- Two muscles in the back of the leg pull on the Achilles tendon as shown in Figure 65.5. What total force do they exert?
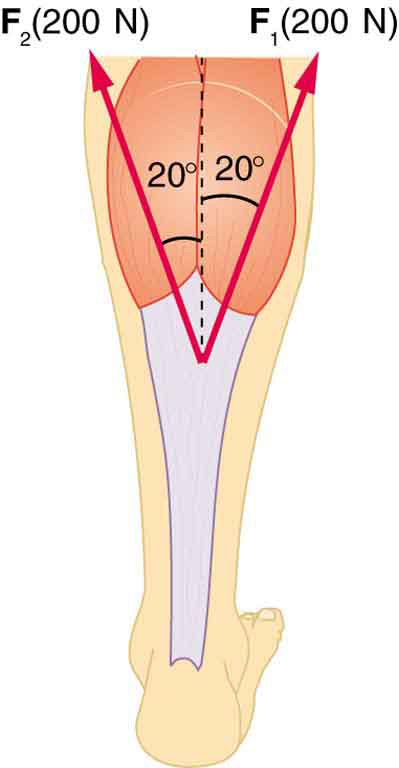
Figure 65.5: The Achilles tendon of the posterior leg serves to attach plantaris, gastrocnemius, and soleus muscles to calcaneus bone. - The upper leg muscle (quadriceps) exerts a force of 1250 N, which is carried by a tendon over the kneecap (the patella) at the angles shown in Figure 65.6. Find the direction and magnitude of the force exerted by the kneecap on the upper leg bone (the femur).
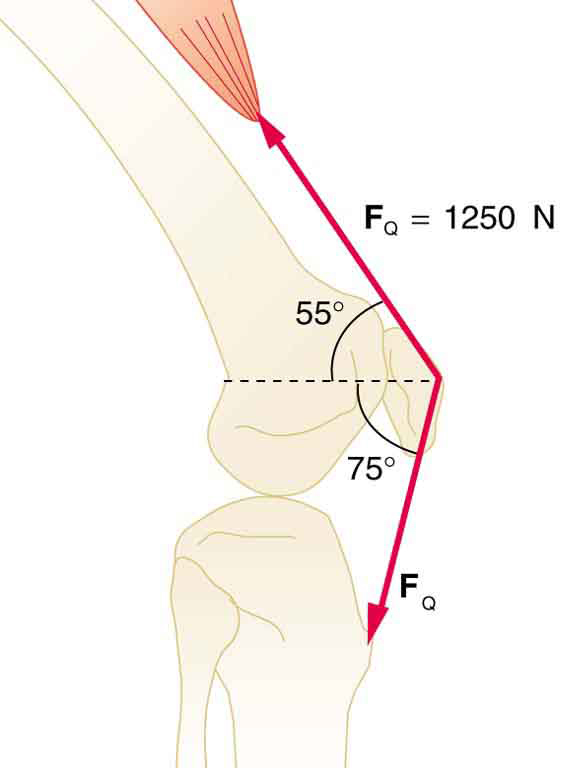
Figure 65.6: The knee joint works like a hinge to bend and straighten the lower leg. It permits a person to sit, stand, and pivot. - A device for exercising the upper leg muscle is shown in Figure 65.7, together with a schematic representation of an equivalent lever system. Calculate the force exerted by the upper leg muscle to lift the mass at a constant speed. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium in Applications of Statistics, Including Problem-Solving Strategies.
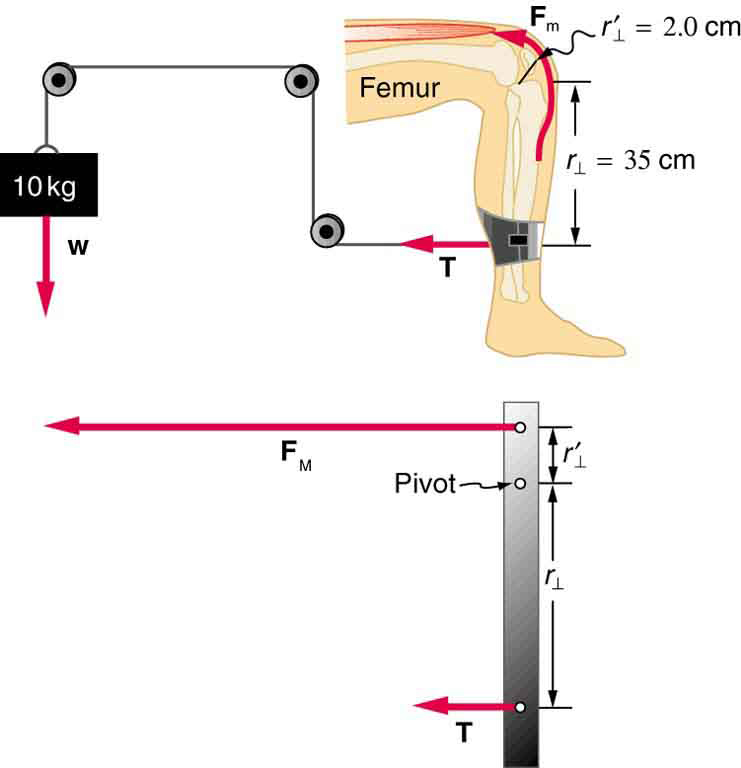
Figure 65.7: A mass is connected by pulleys and wires to the ankle in this exercise device. - A person working at a drafting board may hold her head as shown in Figure 65.8, requiring muscle action to support the head. The three major acting forces are shown. Calculate the direction and magnitude of the force supplied by the upper vertebrae [latex]{\mathbf{\text{F}}}_{\text{V}}[/latex] to hold the head stationary, assuming that this force acts along a line through the center of mass as do the weight and muscle force.
- We analyzed the biceps muscle example with the angle between forearm and upper arm set at [latex]\text{90º}[/latex]. Using the same numbers as in Example 65.1 find the force exerted by the biceps muscle when the angle is [latex]\text{120º}[/latex] and the forearm is in a downward position.
- Even when the head is held erect, as in Figure 65.9, its center of mass is not directly over the principal point of support (the atlanto-occipital joint). The muscles at the back of the neck should therefore exert a force to keep the head erect. That is why your head falls forward when you fall asleep in the class. (a) Calculate the force exerted by these muscles using the information in the figure. (b) What is the force exerted by the pivot on the head?
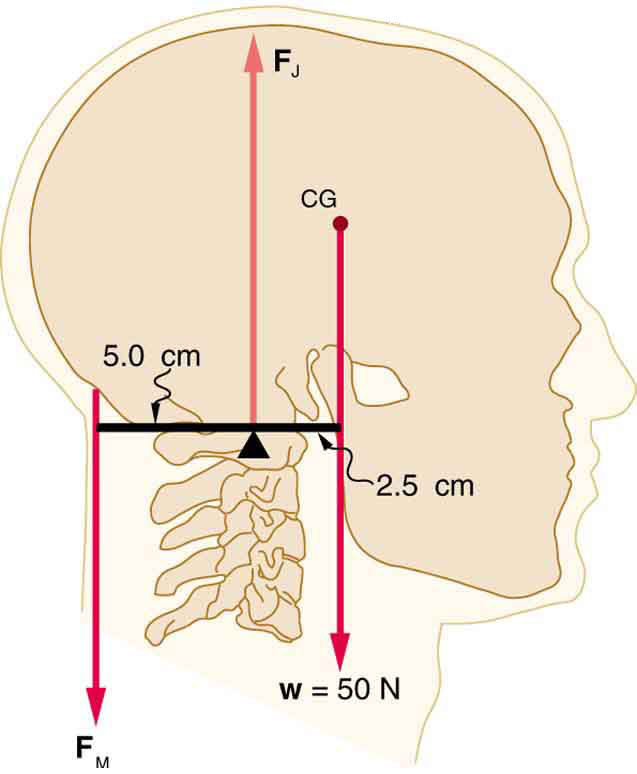
Figure 65.9: The center of mass of the head lies in front of its major point of support, requiring muscle action to hold the head erect. A simplified lever system is shown. - A 75-kg man stands on his toes by exerting an upward force through the Achilles tendon, as in Figure 65.10. (a) What is the force in the Achilles tendon if he stands on one foot? (b) Calculate the force at the pivot of the simplified lever system shown—that force is representative of forces in the ankle joint.
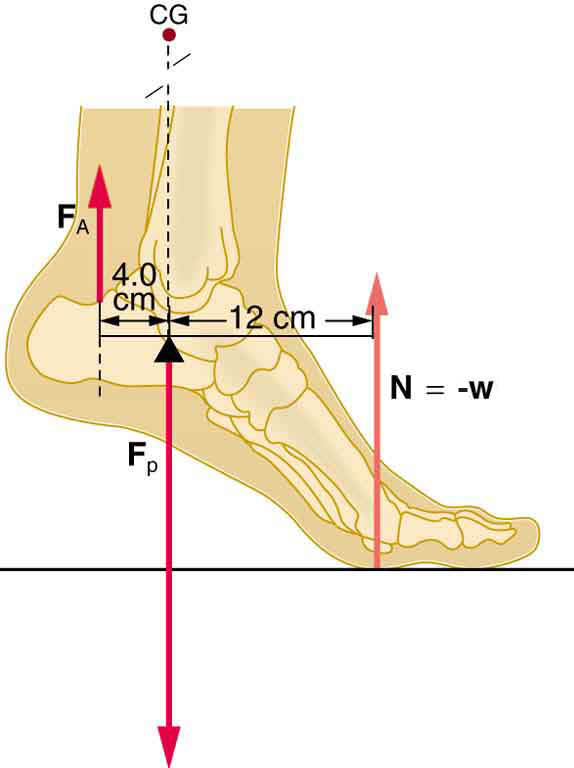
Figure 65.10: The muscles in the back of the leg pull the Achilles tendon when one stands on one’s toes. A simplified lever system is shown. - A father lifts his child as shown in Figure 65.11. What force should the upper leg muscle exert to lift the child at a constant speed?
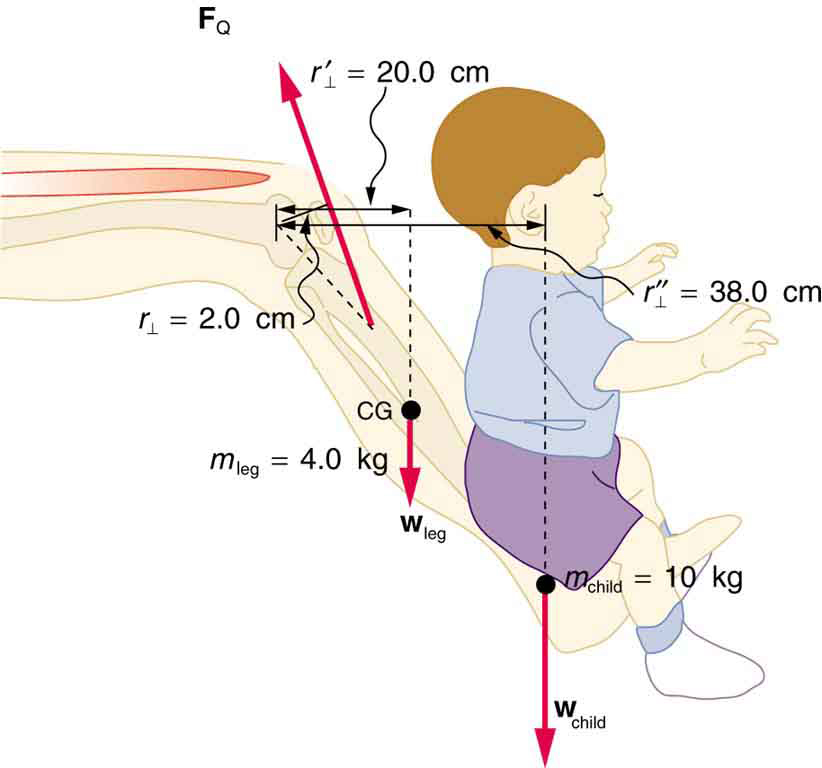
Figure 65.11: A child being lifted by a father’s lower leg. - Unlike most of the other muscles in our bodies, the masseter muscle in the jaw, as illustrated in Figure 65.12, is attached relatively far from the joint, enabling large forces to be exerted by the back teeth. (a) Using the information in the figure, calculate the force exerted by the lower teeth on the bullet. (b) Calculate the force on the joint.
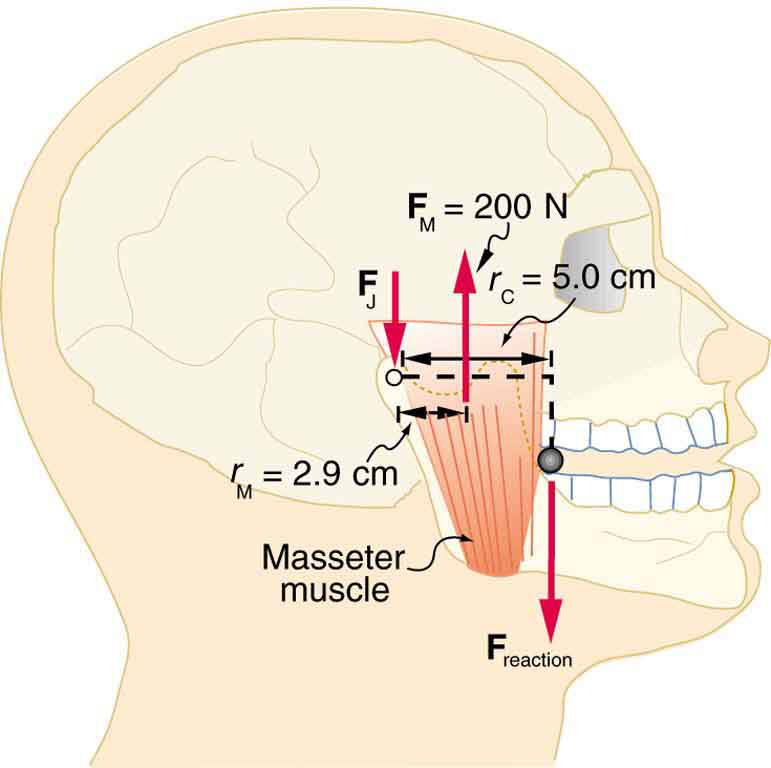
Figure 65.12: A person clenching a bullet between his teeth. - Integrated Concepts Suppose we replace the 4.0-kg book in Exercise 6 above of the biceps muscle with an elastic exercise rope that obeys Hooke’s Law. Assume its force constant [latex]k=\text{600}\phantom{\rule{0.25em}{0ex}}\text{N/m}[/latex]. (a) How much is the rope stretched (past equilibrium) to provide the same force [latex]{F}_{\text{B}}[/latex] as in this example? Assume the rope is held in the hand at the same location as the book. (b) What force is on the biceps muscle if the exercise rope is pulled straight up so that the forearm makes an angle of [latex]\text{25º}[/latex] with the horizontal? Assume the biceps muscle is still perpendicular to the forearm.
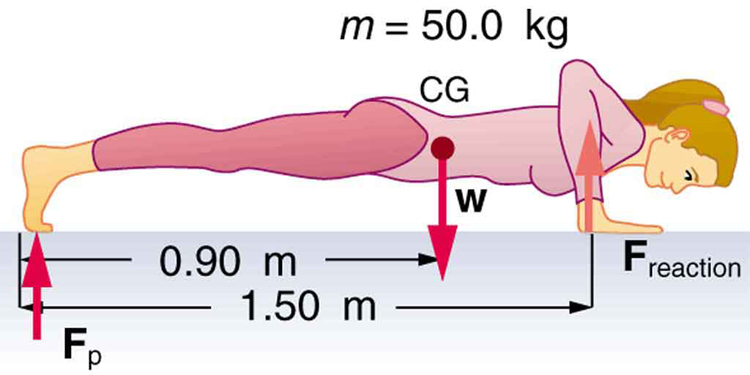
- (a) What force should the woman in Figure 65.13 exert on the floor with each hand to do a push-up? Assume that she moves up at a constant speed. (b) The triceps muscle at the back of her upper arm has an effective lever arm of 1.75 cm, and she exerts force on the floor at a horizontal distance of 20.0 cm from the elbow joint. Calculate the magnitude of the force in each triceps muscle, and compare it to her weight. (c) How much work does she do if her center of mass rises 0.240 m? (d) What is her useful power output if she does 25 pushups in one minute?
- You have just planted a sturdy 2-m-tall palm tree in your front lawn for your mother’s birthday. Your brother kicks a 500 g ball, which hits the top of the tree at a speed of 5 m/s and stays in contact with it for 10 ms. The ball falls to the ground near the base of the tree and the recoil of the tree is minimal. (a) What is the force on the tree? (b) The length of the sturdy section of the root is only 20 cm. Furthermore, the soil around the roots is loose and we can assume that an effective force is applied at the tip of the 20 cm length. What is the effective force exerted by the end of the tip of the root to keep the tree from toppling? Assume the tree will be uprooted rather than bend. (c) What could you have done to ensure that the tree does not uproot easily?
- Unreasonable Results Suppose two children are using a uniform seesaw that is 3.00 m long and has its center of mass over the pivot. The first child has a mass of 30.0 kg and sits 1.40 m from the pivot. (a) Calculate where the second 18.0 kg child must sit to balance the seesaw. (b) What is unreasonable about the result? (c) Which premise is unreasonable, or which premises are inconsistent?
- Construct Your Own Problem Consider a method for measuring the mass of a person’s arm in anatomical studies. The subject lies on her back, extends her relaxed arm to the side and two scales are placed below the arm. One is placed under the elbow and the other under the back of her hand. Construct a problem in which you calculate the mass of the arm and find its center of mass based on the scale readings and the distances of the scales from the shoulder joint. You must include a free body diagram of the arm to direct the analysis. Consider changing the position of the scale under the hand to provide more information, if needed. You may wish to consult references to obtain reasonable mass values.