Work, Energy, and Energy Resources
46 Nonconservative Forces
Learning Objectives
-
Define nonconservative forces and explain how they affect mechanical energy.
-
Use the conservation of energy principle with both conservative and nonconservative forces.
-
Apply the work-energy theorem to biological and everyday systems involving friction.
Nonconservative Forces in Real Life
In biomechanics and health-related systems, forces are not always conservative. A nonconservative force is one where the work done depends on the specific path taken. The most familiar example is friction, which is ever-present in human motion, medical equipment, and the environment.
Consider rubbing your hands together: the longer the path (more rubbing), the more heat (thermal energy) you generate. This is in contrast to conservative forces, like gravity or spring forces, where only the starting and ending points matter.
Because nonconservative forces dissipate energy (often as heat or sound), they do not have an associated potential energy. Their main effect is to change the total mechanical energy of a system.
Friction as a Nonconservative Force
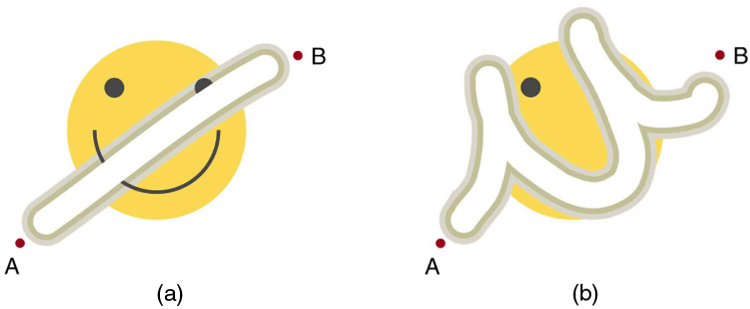
Figure 46.1 shows that the work done erasing the happy face depends on the path the eraser takes. In (a), the eraser moves directly from A to B. In (b), the longer path requires more work and erases more of the face. Friction removes mechanical energy by converting it to thermal energy, which cannot be fully recovered.
Friction is common in the human body. For example:
-
The sliding of tendons over bone surfaces.
-
The resistance of blood flow in vessels.
-
The drag forces encountered during motion in fluid environments.
In these systems, friction removes mechanical energy from the system, often converting it into heat.
How Nonconservative Forces Affect Mechanical Energy
When nonconservative forces are present, mechanical energy is no longer conserved. Suppose you slide a heavy box across the floor. The force of friction slows it down and generates heat, reducing the system’s total mechanical energy.
For example, when a car is brought to a stop by friction on level ground, it loses kinetic energy, which is dissipated as thermal energy, reducing its mechanical energy. Figure 46.2 compares the effects of conservative and nonconservative forces. We often choose to understand simpler systems such as that described in Figure 46.2(a) first before studying more complicated systems as in Figure 46.2(b).
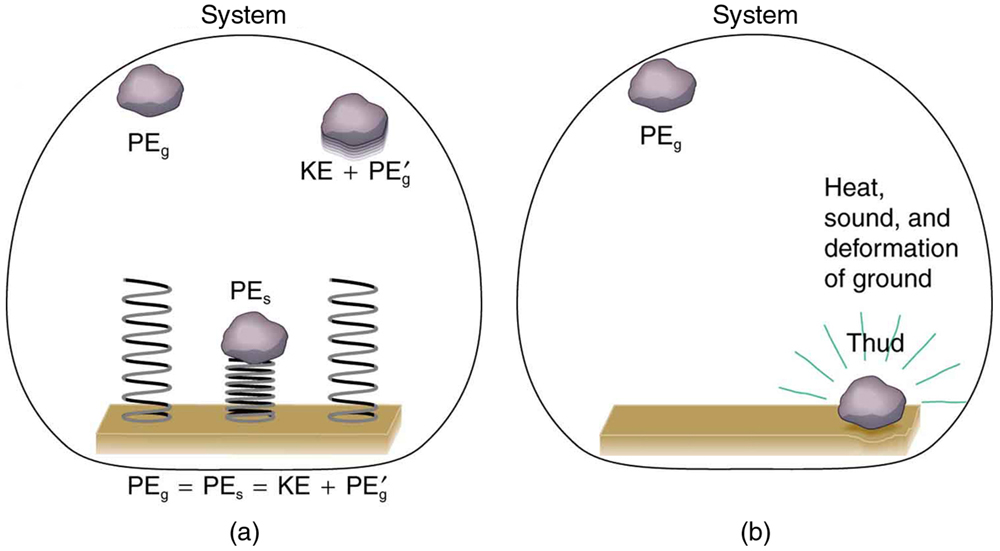 Figure 46.2:
Figure 46.2:
(a) A rock falling onto a spring involves only conservative forces. The rock compresses the spring, storing potential energy, which can propel it back upward. (b) A rock falling onto the ground involves nonconservative forces (friction, deformation), which dissipate mechanical energy as heat and sound.
The Work-Energy Theorem Revisited
We can now update the work-energy theorem to account for both conservative and nonconservative forces. Recall:
[latex]{W}_{\text{net}} = \Delta \text{KE}[/latex]
If both types of forces act:
[latex]{W}{\text{net}} = {W}{\text{c}} + {W}_{\text{nc}}[/latex]
Substituting into the theorem:
[latex]{W}{\text{c}} + {W}{\text{nc}} = \Delta \text{KE}[/latex]
Since conservative work relates to changes in potential energy:
[latex]{W}_{\text{c}} = -\Delta \text{PE}[/latex]
Then:
[latex]{W}_{\text{nc}} = \Delta \text{KE} + \Delta \text{PE}[/latex]
This key result shows that the change in mechanical energy (kinetic + potential) is caused by the work done by nonconservative forces.
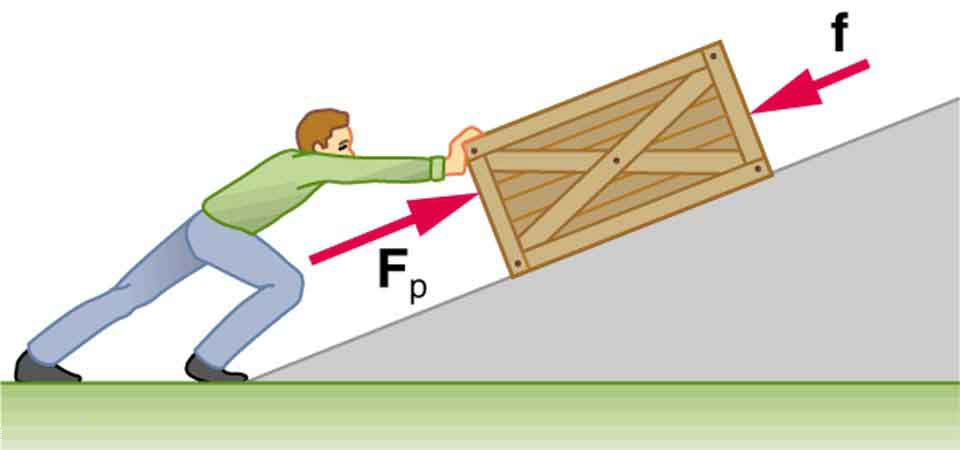
Applying This to a Ramp
In Figure 46.3 a person pushes a crate up a ramp while friction and gravity resist the motion. The person’s applied force does more work than is lost to friction, so the crate gains mechanical energy. If friction were greater, more energy would be lost as heat.
The final mechanical energy of the system can be calculated using:
[latex]{\text{KE}}_{\text{i}} + {\text{PE}}_{\text{i}} + W_{\text{nc}} = {\text{KE}}_{\text{f}} + {\text{PE}}_{\text{f}}[/latex]
This equation is extremely useful in physiology and rehabilitation science. For example:
-
A physical therapist pushing a patient in a wheelchair uphill must overcome both gravity and friction.
-
When a patient walks with a prosthetic leg, some energy is lost to internal friction in the joint components.
Summary of the Effects
-
If [latex]{W}_{\text{nc}} > 0[/latex], mechanical energy increases (external work is added).
-
If [latex]{W}_{\text{nc}} 0[/latex], mechanical energy decreases (energy is dissipated).
-
If [latex]{W}_{\text{nc}} = 0[/latex], mechanical energy is conserved (only conservative forces act).
Key Equation: Mechanical Energy with Nonconservative Forces
[latex]{\text{KE}}_{\text{i}} + {\text{PE}}_{\text{i}} + W_{\text{nc}} = {\text{KE}}_{\text{f}} + {\text{PE}}_{\text{f}}[/latex]
This general energy equation applies whether you are analyzing a limb in motion, a heart valve moving blood, or a person walking uphill.
Would you like a worked example next, perhaps involving a biological or medical system?
Example 46.1: Calculating Distance Traveled: How Far a Baseball Player Slides
Consider the situation shown in Figure 46.4, where a baseball player slides to a stop on level ground. Using energy considerations, calculate the distance the 65.0-kg baseball player slides, given that his initial speed is 6.00 m/s and the force of friction against him is a constant 450 N.
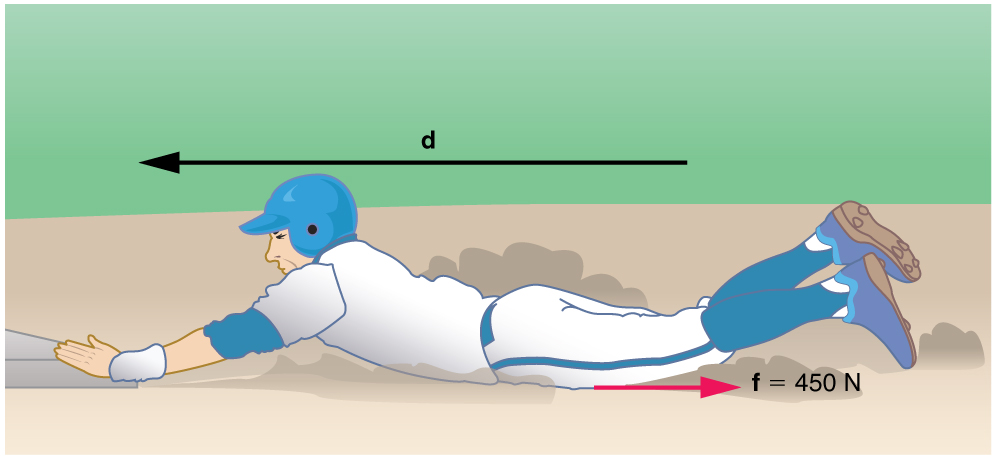
Strategy
Friction stops the player by converting his kinetic energy into other forms, including thermal energy. In terms of the work-energy theorem, the work done by friction, which is negative, is added to the initial kinetic energy to reduce it to zero. The work done by friction is negative, because [latex]\mathbf{\text{f}}[/latex] is in the opposite direction of the motion (that is, [latex]\theta =\text{180º}[/latex], and so [latex]\text{cos}\phantom{\rule{0.25em}{0ex}}\theta =-1[/latex]). Thus [latex]{W}_{\text{nc}}=-\text{fd}[/latex]. The equation simplifies to
or
This equation can now be solved for the distance [latex]d[/latex].
Solution
Solving the previous equation for [latex]d[/latex] and substituting known values yields
Discussion
The most important point of this example is that the amount of nonconservative work equals the change in mechanical energy. For example, you must work harder to stop a truck, with its large mechanical energy, than to stop a mosquito.
Example 46.2: Calculating Distance Traveled: Sliding Up an Incline
Suppose that the player from the previous example is running up a hill having a [latex]5\text{.}\text{00º}[/latex] incline upward with a surface similar to that in the baseball stadium. The player slides with the same initial speed. Determine how far he slides.
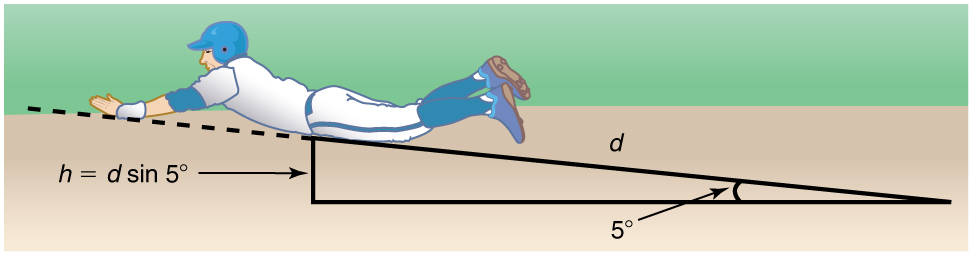
Strategy
In this case, the work done by the nonconservative friction force on the player reduces the mechanical energy he has from his kinetic energy at zero height, to the final mechanical energy he has by moving through distance [latex]d[/latex] to reach height [latex]h[/latex] along the hill, with [latex]h=d\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}5.00º[/latex]. This is expressed by the equation
Solution
The work done by friction is again [latex]{W}_{\text{nc}}=-\text{fd}[/latex]; initially the potential energy is [latex]{\text{PE}}_{i}=\text{mg}\cdot 0=0[/latex] and the kinetic energy is
[latex]{\text{KE}}_{i}=\frac{1}{2}{{\text{mv}}_{i}}^{2}[/latex]; the final energy contributions are
[latex]{\text{KE}}_{f}=0[/latex] for the kinetic energy and [latex]{\text{PE}}_{f}=\text{mgh}=\text{mgd}\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta[/latex] for the potential energy.
Substituting these values gives
Solve this for [latex]d[/latex] to obtain
Discussion
As might have been expected, the player slides a shorter distance by sliding uphill. Note that the problem could also have been solved in terms of the forces directly and the work energy theorem, instead of using the potential energy. This method would have required combining the normal force and force of gravity vectors, which no longer cancel each other because they point in different directions, and friction, to find the net force. You could then use the net force and the net work to find the distance [latex]d[/latex] that reduces the kinetic energy to zero. By applying conservation of energy and using the potential energy instead, we need only consider the gravitational potential energy [latex]\text{mgh}[/latex], without combining and resolving force vectors. This simplifies the solution considerably.
Making Connections: Take-Home Investigation—Determining Friction from the Stopping Distance
This hands-on experiment helps illustrate how gravitational potential energy can be converted into thermal energy through the force of friction, an important concept in biomechanics, rehabilitation, and physical therapy.
Materials:
-
A ruler with a groove (or a ramp)
-
A book (to incline the ruler)
-
A marble
-
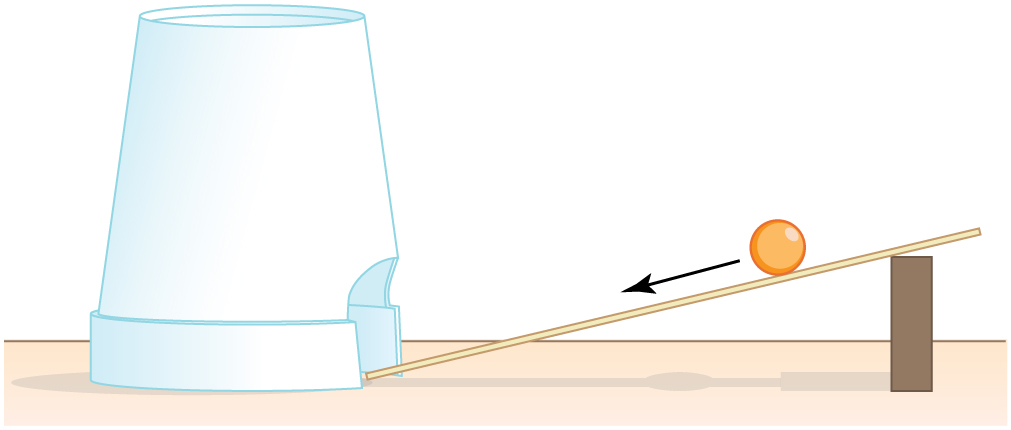
A foam cup with a small hole near the base (see Figure 46.6)
-
A steel marble or ball bearing (optional, for comparison)
Procedure:
-
Position the ruler at an incline using the book like in Figure 46.6.
-
From the 10-cm mark, release the marble so it rolls into the foam cup.
-
Measure how far the cup slides across the surface before coming to rest—this distance is [latex]d[/latex].
-
Repeat the trial from the 20-cm and 30-cm positions and record [latex]d[/latex] for each case.
-
Plot distance moved by the cup versus initial height (position) of the marble on the ramp.
-
Is the plot linear?
-
What does that say about energy conversion?
-
Discussion Questions:
-
What forces caused the cup to stop?
-
What happened to the kinetic energy of the marble at the bottom of the ramp?
-
Was mechanical energy conserved?
Analyzing the Data:
The marble’s kinetic energy at the bottom of the ramp is converted into work done against friction:
[latex]W_{\text{friction}} = f d = \mu_k N d[/latex]
where:
-
[latex]\mu_k[/latex] is the coefficient of kinetic friction,
-
[latex]N[/latex] is the normal force, equal to the weight of the cup plus marble:
[latex]N = (m_{\text{cup}} + m_{\text{marble}})g[/latex], -
[latex]d[/latex] is the distance the cup moves,
-
[latex]f[/latex] is the force of friction:
[latex]f = \mu_k N[/latex].
The initial kinetic energy of the marble is:
[latex]\text{KE}{\text{initial}} = \frac{1}{2} m{\text{marble}} v^2[/latex]
You can estimate [latex]v[/latex] from gravitational potential energy lost during descent:
[latex]m_{\text{marble}}gh = \frac{1}{2} m_{\text{marble}} v^2 \Rightarrow v = \sqrt{2gh}[/latex]
Therefore, using energy conservation:
[latex]\mu_k N d = m_{\text{marble}}gh[/latex]
Solve for [latex]\mu_k[/latex]:
[latex]\mu_k = \frac{m_{\text{marble}}gh}{(m_{\text{cup}} + m_{\text{marble}})g d} = \frac{m_{\text{marble}} h}{(m_{\text{cup}} + m_{\text{marble}}) d}[/latex]
Optional Extension: Steel vs. Glass Marbles
Try repeating the experiment using a steel marble. Ask:
-
Is the marble’s velocity the same at the bottom for the same release height?
-
Does the cup travel a different distance with the heavier marble?
-
Is the distance proportional to the marble’s mass?
This allows you to test whether mass affects energy transfer through friction and how different materials behave in real-life systems—insightful for understanding prosthetics, movement, and rehabilitation equipment.
PhET Explorations: The Ramp
Explore how forces, energy, and work interact in a real-world setting—like pushing a file cabinet up a ramp!
This interactive simulation lets you:
-
Push various household objects up and down an adjustable ramp.
-
Observe how changing the angle of inclination affects the parallel and perpendicular components of the force of gravity.
-
Visualize work done, kinetic energy, and potential energy through real-time graphs.
-
Compare static vs. kinetic friction, and see how mass and surface types affect the difficulty of moving objects—just like in patient handling, physical therapy settings, or biomechanics research.
This is particularly useful for students in:
-
Kinesiology and rehab science (analyzing safe lifting techniques),
-
Occupational therapy (ramp access for assistive devices),
-
Biomechanics (studying force interactions in daily movements).
Section Summary
-
A nonconservative force is a force for which the work done depends on the path taken, not just the starting and ending points.
-
Friction is a key example of a nonconservative force. It transforms mechanical energy (like motion) into thermal energy, which is generally not recoverable in biological or mechanical systems.
-
The work [latex]{W}_{\text{nc}}[/latex] done by a nonconservative force changes a system’s mechanical energy. This relationship is expressed as:
[latex]{W}_{\text{nc}} = \Delta \text{KE} + \Delta \text{PE}[/latex]
or equivalently,
[latex]{\text{KE}}_{\text{i}} + {\text{PE}}_{\text{i}} + W_{\text{nc}} = {\text{KE}}_{\text{f}} + {\text{PE}}_{\text{f}}[/latex]
-
In many biomechanical and clinical situations, both conservative (like gravity or muscle elasticity) and nonconservative (like joint friction or air resistance) forces act. You can still use energy conservation principles to solve problems, using known potential energy expressions for conservative forces and accounting for work by nonconservative forces, rather than resorting to full force diagrams or Newton’s second law.
Problems & Exercises
- A 60.0-kg skier with an initial speed of 12.0 m/s coasts up a 2.50-m-high rise as shown in Figure 46.8. Find her final speed at the top, given that the coefficient of friction between her skis and the snow is 0.0800. (Hint: Find the distance traveled up the incline assuming a straight-line path as shown in the figure.)
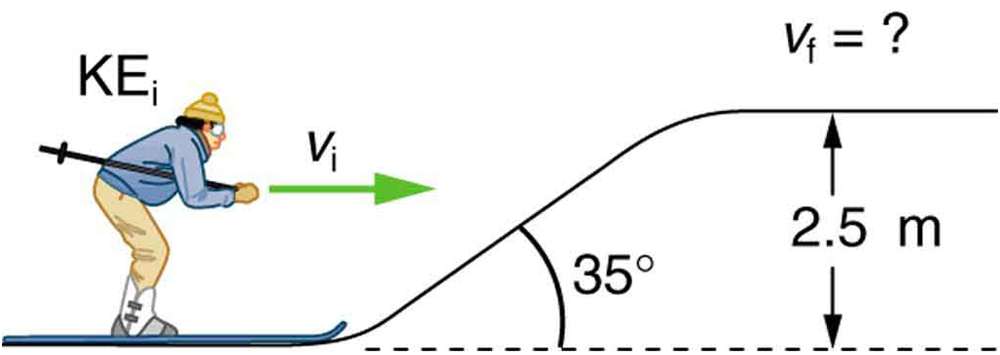
Figure 46.8: The skier’s initial kinetic energy is partially used in coasting to the top of a rise. - (a) How high a hill can a car coast up (engine disengaged) if work done by friction is negligible and its initial speed is 110 km/h? (b) If, in actuality, a 750-kg car with an initial speed of 110 km/h is observed to coast up a hill to a height 22.0 m above its starting point, how much thermal energy was generated by friction? (c) What is the average force of friction if the hill has a slope [latex]2\text{.}5º[/latex] above the horizontal?
Glossary
- nonconservative force
- a force whose work depends on the path followed between the given initial and final configurations
- friction
- the force between surfaces that opposes one sliding on the other; friction changes mechanical energy into thermal energy
a force whose work depends on the path followed between the given initial and final configurations
a force past each other of objects that are touching; examples include rough surfaces and air resistance

