"

Uniform Circular Motion and Gravitation

37 Centripetal Force

Learning Objectives

  • Calculate coefficient of friction on a car tire.
  • Calculate ideal speed and angle of a car on a turn.

 

Any force—or combination of forces—that produces a centripetal (radial) acceleration is considered a centripetal force. This includes many familiar scenarios, such as:

  • The tension in the string of a tetherball,

  • The gravitational force between the Earth and Moon,

  • Friction between roller skates and the rink floor,

  • The normal and frictional forces on a car on a banked curve,

  • The contact forces on a sample tube in a spinning centrifuge.

The centripetal force is always directed toward the center of curvature, just like the centripetal acceleration [latex]a_c[/latex] it causes.

According to Newton’s second law:

[latex]\text{net }F = ma.[/latex]

In the case of uniform circular motion, the acceleration is centripetal, so:

[latex]F_c = ma_c.[/latex]

Using the known formulas for centripetal acceleration:

[latex]a_c = \frac{v^2}{r} \quad \text{or} \quad a_c = r\omega^2,[/latex]

we can derive the corresponding expressions for centripetal force:

[latex]F_c = m\frac{v^2}{r} \quad \text{or} \quad F_c = mr\omega^2.[/latex]

These equations show that the required centripetal force increases with:

  • The square of the speed [latex]v[/latex],

  • The mass [latex]m[/latex],

  • And inversely with the radius [latex]r[/latex] (in the linear case).

You can use whichever form is more appropriate based on whether the situation involves linear speed [latex]v[/latex] or angular velocity [latex]\omega[/latex].

Relationship Between Force and Curve Radius

Solving for the radius [latex]r[/latex] in the first expression gives:

[latex]r = \frac{mv^2}{F_c}.[/latex]

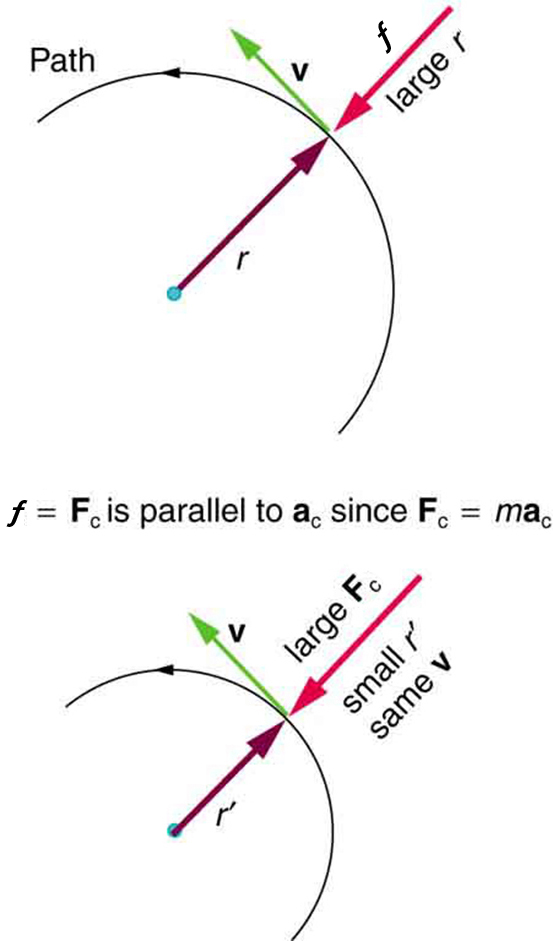
This result highlights an important physical insight: for a given mass and speed, a larger centripetal force results in a smaller radius of curvature—meaning a tighter turn or sharper curve.

Direction of Centripetal Force

Centripetal force is always:

  • Perpendicular to the instantaneous velocity of the object,

  • Directed inward, toward the center of the circular path.

Because velocity is tangent to the path and acceleration is radial (toward the center), the net force causing circular motion must also point inward.

Figure 37.1 illustrates a scenario in which friction supplies the necessary centripetal force for a car turning along a curve. The larger the required centripetal force [latex]F_c[/latex], the smaller the radius [latex]r[/latex] of the turn. That is why higher speeds or sharper curves require more friction to prevent slipping.

The given figure consists of two semicircles, one over the other. The top semicircle is bigger and the one below is smaller. In both the figures, the direction of the path is given along the semicircle in the counter-clockwise direction. A point is shown on the path, where the radius from the circle, r, is shown with an arrow from the center of the circle. At the same point, the centripetal force is shown in the opposite direction to that of radius arrow. The velocity, v, is shown along this point in the left upward direction and is perpendicular to the force. In both the figures, the velocity is same, but the radius is smaller and centripetal force is larger in the lower figure.
Figure 37.1: The frictional force supplies the centripetal force and is numerically equal to it. Centripetal force is perpendicular to velocity and causes uniform circular motion. The larger the [latex]{\text{F}}_{\text{c}}[/latex], the smaller the radius of curvature [latex]r[/latex] and the sharper the curve. The second curve has the same [latex]v[/latex], but a larger [latex]{\text{F}}_{\text{c}}[/latex] produces a smaller [latex]r\prime [/latex].

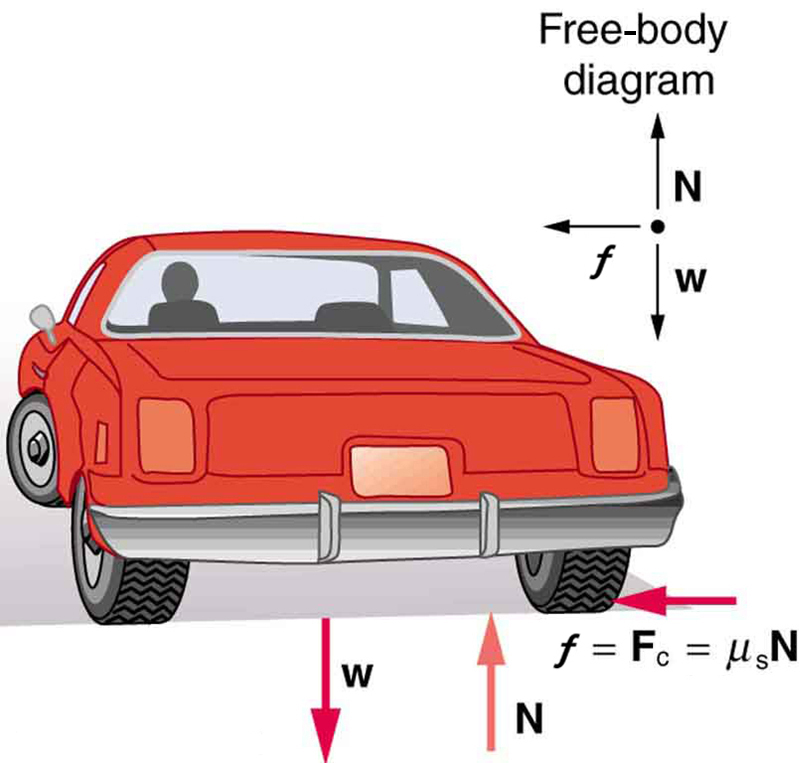
Example 37.1: What Coefficient of Friction Do Car Tires Need on a Flat Curve?

  1. Calculate the centripetal force exerted on a 900 kg car that negotiates a 500 m radius curve at 25.0 m/s.
  2. Assuming an unbanked curve, find the minimum static coefficient of friction, between the tires and the road, static friction being the reason that keeps the car from slipping (see Figure 37.2).

Strategy and Solution for (a)

We know that
[latex]{F}_{\text{c}}=\frac{{\mathrm{mv}}^{\text{2}}}{r}[/latex]. Thus,

[latex]{F}_{\text{c}}=\frac{{\mathrm{mv}}^{\text{2}}}{r}=\frac{\left(\text{900 kg}\right){\left(\text{25.0 m/s}\right)}^{\text{2}}}{\left(\text{500 m}\right)}=\text{1125 N.}[/latex]

Strategy for (b)

Figure 37.2 shows the forces acting on the car on an unbanked (level ground) curve. Friction is to the left, keeping the car from slipping, and because it is the only horizontal force acting on the car, the friction is the centripetal force in this case. We know that the maximum static friction (at which the tires roll but do not slip) is [latex]{\mu }_{\text{s}}N[/latex], where [latex]{\mu }_{\text{s}}[/latex] is the static coefficient of friction and N is the normal force. The normal force equals the car’s weight on level ground, so that

[latex]N=\mathit{mg}[/latex]. Thus the centripetal force in this situation is

[latex]{F}_{\text{c}}=f={\mu }_{\text{s}}N={\mu }_{\text{s}}\text{mg}\text{.}[/latex]

Now we have a relationship between centripetal force and the coefficient of friction. Using the first expression for [latex]{F}_{\text{c}}[/latex] from the equation

[latex]\begin{array}{c}{F}_{\text{c}}=m\frac{{v}^{2}}{r}\\ {F}_{\text{c}}=\text{mr}{\omega }^{2}\end{array}[/latex],
[latex]m\frac{{v}^{2}}{r}={\mu }_{\text{s}}\text{mg}\text{.}[/latex]

We solve this for [latex]{\mu }_{\text{s}}[/latex], noting that mass cancels, and obtain

[latex]{\mu }_{\text{s}}=\frac{{v}^{2}}{\text{rg}}\text{.}[/latex]

Solution for (b)

Substituting the knowns,

[latex]{\mu }_{\text{s}}=\frac{\left(\text{25.0 m/s}\right)^{2}}{\left(\text{500 m}\right)\left(9\text{.}{\text{80 m/s}}^{2}\right)}=0\text{.}\text{13}\text{.}[/latex]

(Because coefficients of friction are approximate, the answer is given to only two digits.)

Discussion

We could also solve part (a) using the first expression in [latex]\begin{array}{c}{F}_{\text{c}}=m\frac{{v}^{2}}{r}\\ {F}_{\text{c}}=\text{mr}{\omega }^{2}\end{array},[/latex] because [latex]m,[/latex][latex]v,[/latex] and [latex]r[/latex] are given. The coefficient of friction found in part (b) is much smaller than is typically found between tires and roads. The car will still negotiate the curve if the coefficient is greater than 0.13, because static friction is a responsive force, being able to assume a value less than but no more than [latex]{\mu }_{\text{s}}N[/latex]. A higher coefficient would also allow the car to negotiate the curve at a higher speed, but if the coefficient of friction is less, the safe speed would be less than 25 m/s. Note that mass cancels, implying that in this example, it does not matter how heavily loaded the car is to negotiate the turn. Mass cancels because friction is assumed proportional to the normal force, which in turn is proportional to mass. If the surface of the road were banked, the normal force would be less as will be discussed below.

In the given figure, a car is shown from the back, which is turning to the left. The weight, w, of the car is shown with a down arrow and N with an up arrow at the back of the car. At the right rear wheel, centripetal force is shown along with its equation formula in a leftward horizontal arrow. The free-body diagram shows three vectors, one upward, depicting N, one downward, depicting w, and one leftward, depicting centripetal force.
Figure 37.2: This car on level ground is moving away and turning to the left. The centripetal force causing the car to turn in a circular path is due to friction between the tires and the road. A minimum coefficient of friction is needed, or the car will move in a larger-radius curve and leave the roadway.

 

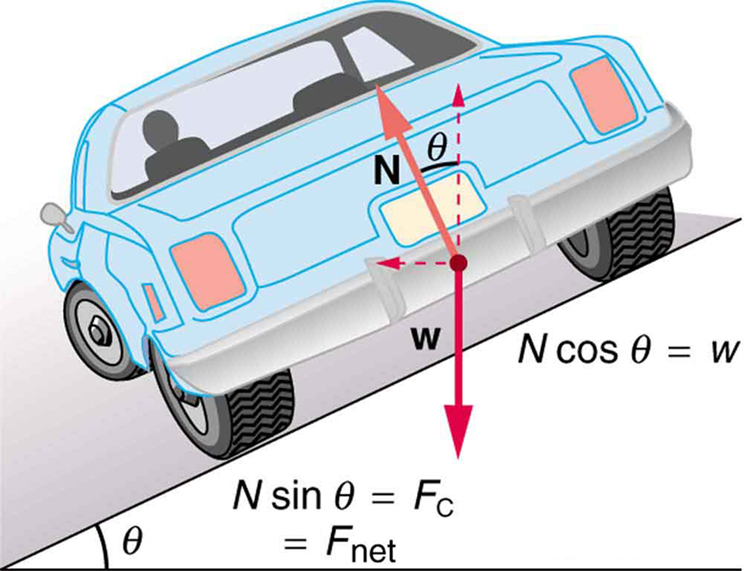
Banked Curves: Ideal Banking Without Friction

In many situations—such as race tracks and curved highway ramps—the road is tilted or banked to help vehicles safely navigate curves at higher speeds. The angle of the banking, [latex]\theta[/latex], allows a component of the normal force to contribute to the centripetal force required for circular motion. This reduces (or can eliminate) reliance on friction between the tires and the road.

The Ideal Banking Angle

An ideally banked curve is one in which the road’s banking angle [latex]\theta[/latex] is designed for a specific speed [latex]v[/latex] and curve radius [latex]r[/latex], such that no friction is needed to maintain the turn. This scenario is shown in Figure 37.3.

In this frictionless case:

  • The vertical component of the normal force balances the gravitational force.

  • The horizontal component of the normal force provides the required centripetal force.

We analyze the system using a free-body diagram with two forces:

  1. The gravitational force: [latex]mg[/latex], acting vertically downward.

  2. The normal force: [latex]N[/latex], perpendicular to the road surface.

We decompose [latex]N[/latex] into components:

  • Horizontal: [latex]N \sin \theta[/latex]

  • Vertical: [latex]N \cos \theta[/latex]

Step 1: Vertical Force Balance

There is no vertical acceleration, so the vertical forces must balance:

[latex]N \cos \theta = mg \tag{1}[/latex]

Step 2: Horizontal Force Provides Centripetal Acceleration

The horizontal component of the normal force supplies the centripetal force:

[latex]N \sin \theta = \frac{mv^2}{r} \tag{2}[/latex]

Step 3: Eliminate [latex]N[/latex]

Solve equation (1) for [latex]N[/latex]:

[latex]N = \frac{mg}{\cos \theta}[/latex]

Substitute into equation (2):

[latex]\frac{mg}{\cos \theta} \sin \theta = \frac{mv^2}{r}[/latex]

Simplify:

[latex]mg \tan \theta = \frac{mv^2}{r}[/latex]

Cancel [latex]m[/latex]:

[latex]g \tan \theta = \frac{v^2}{r}[/latex]

Solving for [latex]\theta[/latex]:

[latex]\tan \theta = \frac{v^2}{rg}[/latex]

[latex]\theta = \tan^{-1} \left( \frac{v^2}{rg} \right) \tag{3}[/latex]

This is the condition for an ideally banked curve, where no friction is required.

Interpreting the Result

The angle [latex]\theta[/latex] depends only on:

  • Speed: [latex]v[/latex]

  • Radius of the curve: [latex]r[/latex]

  • Gravitational acceleration: [latex]g[/latex]

Key Insight:

  • A higher speed [latex]v[/latex] or a smaller radius [latex]r[/latex] requires a steeper banking angle.

  • The result is independent of mass, so the same ideal angle applies to cars of all sizes.

In this figure, a car from the backside is shown, turning to the left, on a slope angling downward to the left. A point in the middle of the back of the car is shown which shows one downward vector depicting weight, w, and an upward arrow depicting force N, which is a linear line along the car and is at an angle theta with the straight up arrow. The slope is at an angle theta with the horizontal surface below the slope. The force values, N multipliy sine theta equals to centripetal force, the net force on the car and N cosine theta equal to w are given below the car.
Figure 37.3: The car on this banked curve is turning to the left. The normal force [latex]N[/latex] is angled from the vertical and is responsible for providing both vertical support and horizontal centripetal force. The ideal banking angle [latex]\theta[/latex] ensures that the car can make the turn at a specific speed without any friction.

Example 37.2: What Is the Ideal Speed to Take a Steeply Banked Tight Curve?

Curves on some test tracks and race courses, such as the Daytona International Speedway in Florida, are very steeply banked. This banking, with the aid of tire friction and very stable car configurations, allows the curves to be taken at very high speed. To illustrate, calculate the speed at which a 100 m radius curve banked at 65.0° should be driven if the road is frictionless.

Strategy

We first note that all terms in the expression for the ideal angle of a banked curve except for speed are known; thus, we need only rearrange it so that speed appears on the left-hand side and then substitute known quantities.

Solution

Starting with

[latex]\text{tan}\phantom{\rule{0.25em}{0ex}}\theta =\frac{{v}^{2}}{\text{rg}}[/latex]

we get

[latex]v=(\text{rg}\phantom{\rule{0.25em}{0ex}}\text{tan}\phantom{\rule{0.25em}{0ex}}\theta {)}^{1/2}\text{.}[/latex]

Noting that tan 65.0º = 2.14, we obtain

[latex]\begin{array}{lll}v& =& {\left[\left(\text{100 m}\right)\left(9.80 m{\text{/s}}^{2}\right)\left(2\text{.}\text{14}\right)\right]}^{1/2}\\ & =& \text{45.8 m/s.}\end{array}[/latex]

Discussion

This is just about 165 km/h, consistent with a very steeply banked and rather sharp curve. Tire friction enables a vehicle to take the curve at significantly higher speeds.

Calculations similar to those in the preceding examples can be performed for a host of interesting situations in which centripetal force is involved—a number of these are presented in this chapter’s Problems and Exercises.

Take-Home Experiment

Ask a friend or relative to swing a golf club or a tennis racquet in a circular arc. Choose a reference point at the end of the club or racquet (e.g., the tip), and follow these steps:

  1. Measure the radius of the swing ([latex]r[/latex]) — this is the approximate distance from the point of rotation (usually the shoulder or wrist) to the tip.

  2. Record the time it takes to complete one full swing (use a stopwatch or slow-motion video to measure [latex]T[/latex]).

  3. Calculate the speed of the tip using:

    [latex]v = \frac{2\pi r}{T}[/latex]

  4. Calculate the centripetal acceleration using:

    [latex]a_c = \frac{v^2}{r}[/latex]

Optional: Use slow-motion recording to improve measurement accuracy and estimate the arc more precisely.

PhET Explorations: Gravity and Orbits

Move the sun, earth, moon and space station to see how it affects their gravitational forces and orbital paths. Visualize the sizes and distances between different heavenly bodies, and turn off gravity to see what would happen without it!

Section Summary

  • Centripetal force [latex]{F}_{\text{c}}[/latex] is any net force that causes uniform circular motion. It always points toward the center of the circle—hence the term “center-seeking”—and is always perpendicular to the object’s instantaneous linear velocity [latex]v[/latex].

    According to Newton’s second law, the magnitude of the centripetal force is given by:

    [latex]{F}{\text{c}} = m a{\text{c}}[/latex]

    This can be expressed using the formulas for centripetal acceleration:

    • In terms of linear velocity:

      [latex]{F}_{\text{c}} = m \frac{v^2}{r}[/latex]

    • In terms of angular velocity:

      [latex]{F}_{\text{c}} = m r \omega^2[/latex]

    Use whichever expression is most convenient, depending on whether linear velocity [latex]v[/latex] or angular velocity [latex]\omega[/latex] is known.

Conceptual Questions

  1. If you wish to reduce the stress (which is related to centripetal force) on high-speed tires, would you use large- or small-diameter tires? Explain.
  2. Define centripetal force. Can any type of force (for example, tension, gravitational force, friction, and so on) be a centripetal force? Can any combination of forces be a centripetal force?
  3. If centripetal force is directed toward the center, why do you feel that you are ‘thrown’ away from the center as a car goes around a curve? Explain.
  4. Race car drivers routinely cut corners as shown in Figure 37.5. Explain how this allows the curve to be taken at the greatest speed.
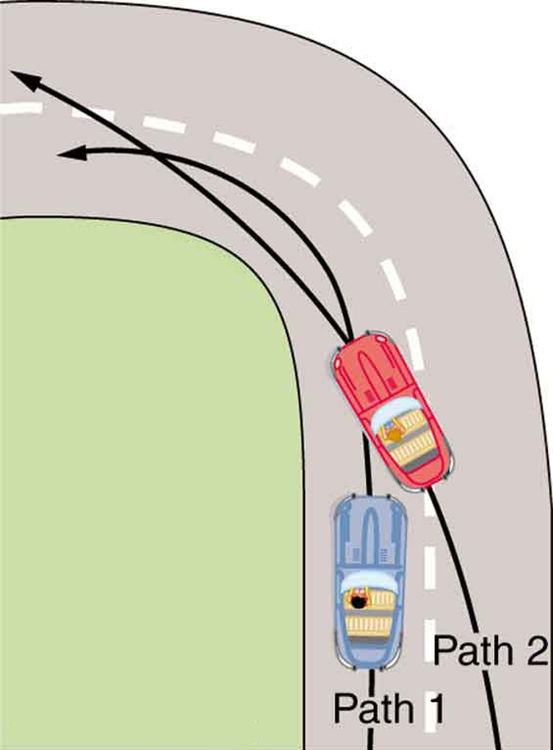
    In the figure, two paths are shown inside a race track through a steep curve, approximately equal to ninety degrees. Two cars are shown. One car is on the path one, which is the inside path along the track. The path of this car is shown with an arrow through the inside path. The second car is shown overtaking the first car, while taking a left turn, showing it to be crossing into the inside path from the second path. The path of this car is also shown with an arrow throughout.
    Figure 37.5: Two paths around a race track curve are shown. Race car drivers will take the inside path (called cutting the corner) whenever possible because it allows them to take the curve at the highest speed.
  5. A number of amusement parks have rides that make vertical loops like the one shown in Figure 37.6. For safety, the cars are attached to the rails in such a way that they cannot fall off. If the car goes over the top at just the right speed, gravity alone will supply the centripetal force. What other force acts and what is its direction if:
    1. The car goes over the top at faster than this speed?
    2. The car goes over the top at slower than this speed?
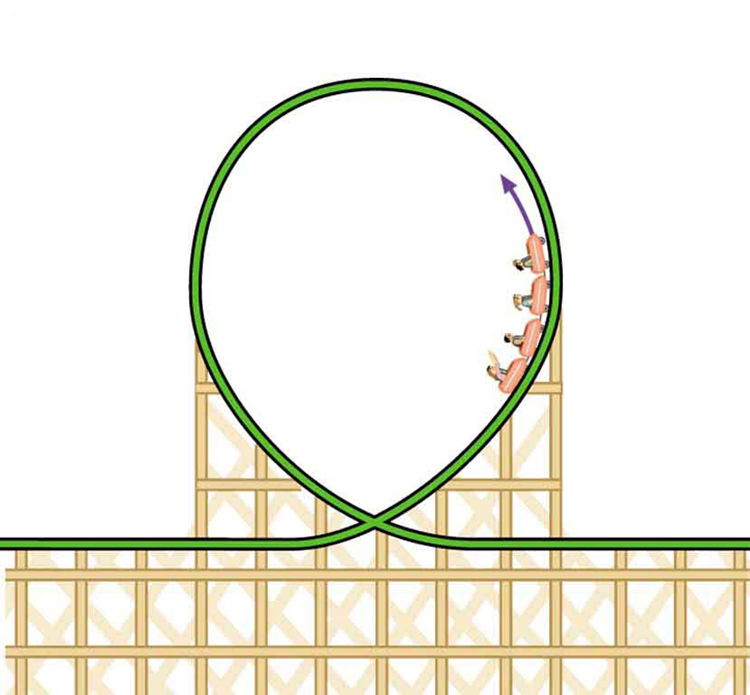
      In the given line diagram, a circular amusement ride is shown from the front with a boat having four people seated in it going upward from the left to the right. The ride starts from the left in a horizontal direction, then goes upward, then turns sideways to the left, comes down from the right and moves horizontal to the right and then ends. It looks like a single knot of a thread, viewed from sideways. Some square iron blocks are also shown below the ride path.
      Figure 37.6: Amusement rides with a vertical loop are an example of a form of curved motion.

      What is the direction of the force exerted by the car on the passenger as the car goes over the top of the amusement ride pictured in Figure 37.6 under the following circumstances:

      1. The car goes over the top at such a speed that the gravitational force is the only force acting?
      2. The car goes over the top faster than this speed?
      3. The car goes over the top at slower than this speed?
  6. As a skater forms a circle, what force is responsible for making her turn? Use a free body diagram in your answer.
  7. Suppose a child is riding on a merry-go-round at a distance about halfway between its center and edge. She has a lunch box resting on wax paper, so that there is very little friction between it and the merry-go-round. Which path shown in Figure 37.7 will the lunch box take when she lets go? The lunch box leaves a trail in the dust on the merry-go-round. Is that trail straight, curved to the left, or curved to the right? Explain your answer.
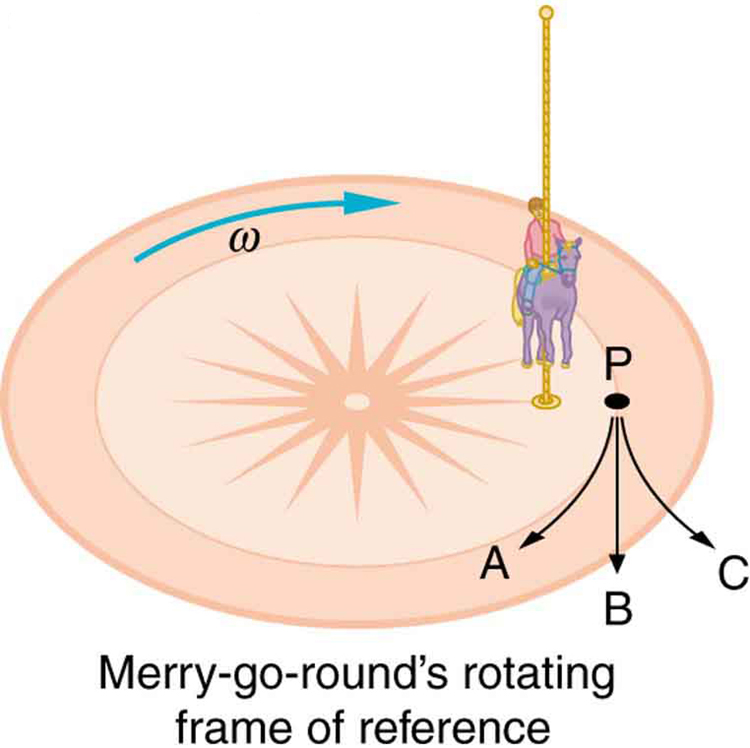
    The given figure shows the circular base of a merry-go-round, whose angular velocity is clockwise, shown here with an arrow. A single horse is shown on whom a child is sitting, with a vertical line shown passed through her, which goes from the bottom of the merry-go-round to the top of it. A point P is shown alongside the horse, through which three arrows in downward three directions are shown which depicts the three possible path of the fall of the lunch box.
    Figure 37.7: A child riding on a merry-go-round releases her lunch box at point P. This is a view from above the clockwise rotation. Assuming it slides with negligible friction, will it follow path A, B, or C, as viewed from Earth’s frame of reference? What will be the shape of the path it leaves in the dust on the merry-go-round?

     

  8. Do you feel yourself thrown to either side when you negotiate a curve that is ideally banked for your car’s speed? What is the direction of the force exerted on you by the car seat?
  9. Suppose a mass is moving in a circular path on a frictionless table as shown in figure. In the Earth’s frame of reference, there is no centrifugal force pulling the mass away from the centre of rotation, yet there is a very real force stretching the string attaching the mass to the nail. Using concepts related to centripetal force and Newton’s third law, explain what force stretches the string, identifying its physical origin.
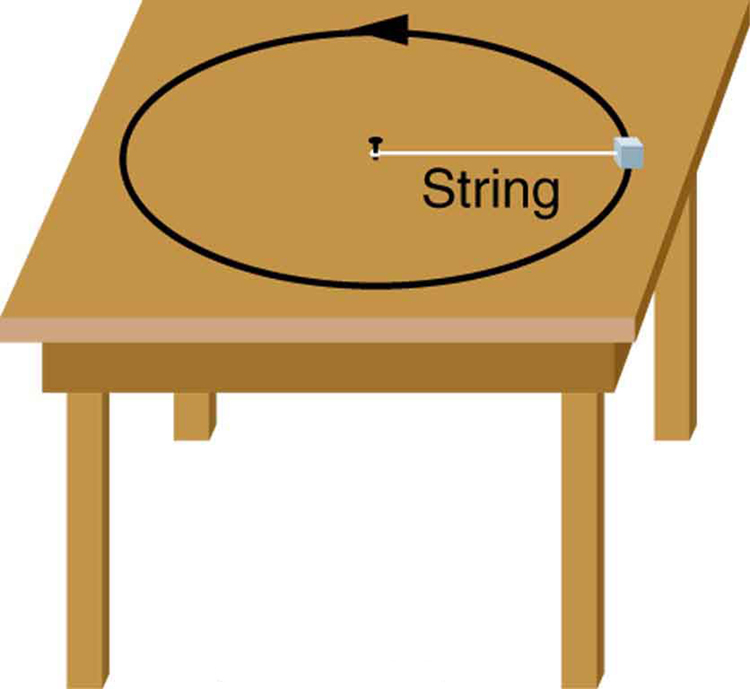
    In the figure a table is shown. On the table a mass is attached to a nail at the center with the help of a string. The mass is moving on a circular path in counterclockwise direction.
    Figure 37.8: A mass attached to a nail on a frictionless table moves in a circular path. The force stretching the string is real and not fictional. What is the physical origin of the force on the string?

Problems Exercise

  1. (a) A 22.0 kg child is riding a playground merry-go-round that is rotating at 40.0 rev/min. What centripetal force must she exert to stay on if she is 1.25 m from its center? (b) What centripetal force does she need to stay on an amusement park merry-go-round that rotates at 3.00 rev/min if she is 8.00 m from its center? (c) Compare each force with her weight.
  2. Calculate the centripetal force on the end of a 100 m (radius) wind turbine blade that is rotating at 0.5 rev/s. Assume the mass is 4 kg.
  3. What is the ideal banking angle for a gentle turn of 1.20 km radius on a highway with a 105 km/h speed limit (about 65 mi/h), assuming everyone travels at the limit?
  4. What is the ideal speed to take a 100 m radius curve banked at a 20.0° angle?
  5. (a) What is the radius of a bobsled turn banked at 75.0° and taken at 30.0 m/s, assuming it is ideally banked? (b) Calculate the centripetal acceleration. (c) Does this acceleration seem large to you?
  6. Part of riding a bicycle involves leaning at the correct angle when making a turn, as seen in Figure 37.9. To be stable, the force exerted by the ground must be on a line going through the center of gravity. The force on the bicycle wheel can be resolved into two perpendicular components—friction parallel to the road (this must supply the centripetal force), and the vertical normal force (which must equal the system’s weight).
  7. (a) Show that [latex]\theta[/latex] (as defined in the figure) is related to the speed [latex]v[/latex] and radius of curvature [latex]r[/latex] of the turn in the same way as for an ideally banked roadway—that is, (b) Calculate [latex]\theta[/latex] for a 12.0 m/s turn of radius 30.0 m (as in a race).
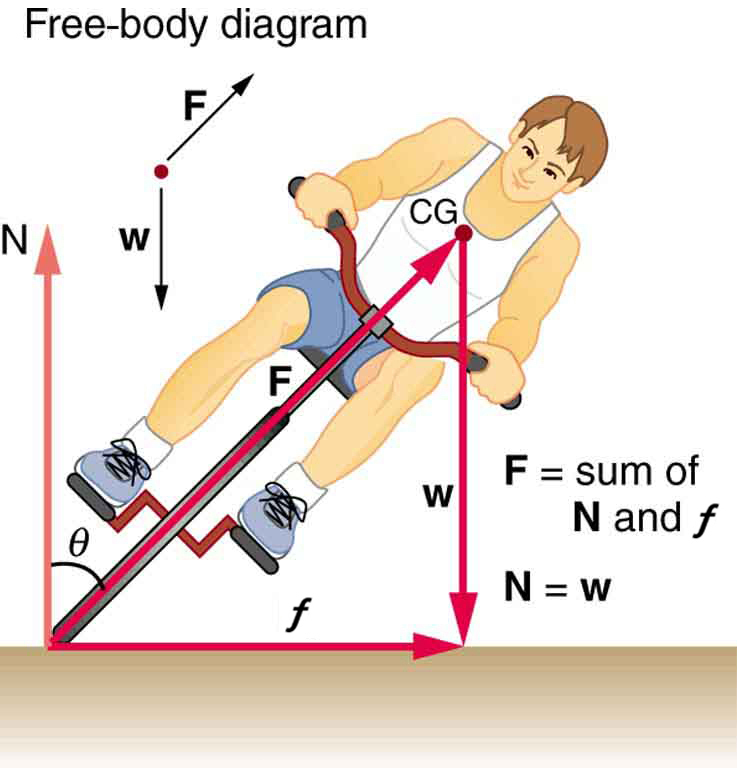
    The given figure shows a boy riding a bicycle, from the front. The boy is sliding leftward to his left. Three vectors are shown. One is from the bottom the front cycle wheel to the right depicting centripetal force, another one is from the same point drawn vertically upward showing the force N, making an angle theta with the slope of the front cycle wheel. The third vector is drawn from the chest of the boy to vertically downward to the bottom showing his weight, w. An arrow from the bottom of the wheel to the chest point of the boy is also shown depicting the slope of the bicycle with force F exerting on it. A free-body diagram is also given alongside the figure showing the direction of weight and force vectors. And the values of net F equals to sum of N and centripetal force, and N equals to weight W also given alongside on the right.
    Figure 37.9: A bicyclist negotiating a turn on level ground must lean at the correct angle—the ability to do this becomes instinctive. The force of the ground on the wheel needs to be on a line through the center of gravity. The net external force on the system is the centripetal force. The vertical component of the force on the wheel cancels the weight of the system while its horizontal component must supply the centripetal force. This process produces a relationship among the angle [latex]\theta [/latex], the speed [latex]v[/latex], and the radius of curvature [latex]r[/latex] of the turn similar to that for the ideal banking of roadways.

  8. A large centrifuge, like the one shown in Figure 37.10(a), is used to expose aspiring astronauts to accelerations similar to those experienced in rocket launches and atmospheric reentries. (a) At what angular velocity is the centripetal acceleration [latex]\mathrm{10}\phantom{\rule{0.25em}{0ex}}g[/latex] if the rider is 15.0 m from the center of rotation? (b) The rider’s cage hangs on a pivot at the end of the arm, allowing it to swing outward during rotation as shown in Figure 37.10(b). At what angle [latex]\theta[/latex] below the horizontal will the cage hang when the centripetal acceleration is [latex]\mathrm{10}\phantom{\rule{0.25em}{0ex}}g[/latex] ? (Hint: The arm supplies centripetal force and supports the weight of the cage. Draw a free body diagram of the forces to see what the angle [latex]\theta[/latex] should be.)
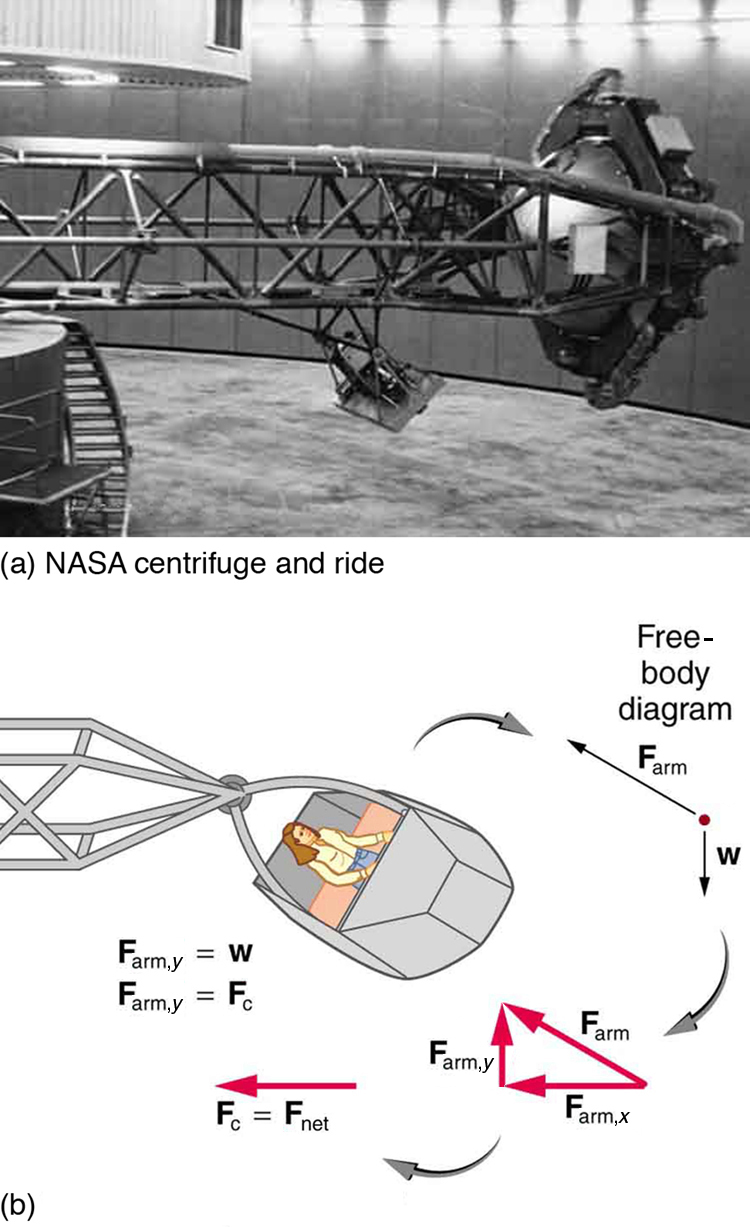
    Figure a shows a NASA centrifuge n a big hall. In figure b, there is a girl sitting in the cage of the centrifuge. The centripetal force on the cage is directed toward left. The direction of the weight of the cage is downward and the force on the arm is directed in north-west direction.
    Figure 37.10: (a) NASA centrifuge used to subject trainees to accelerations similar to those experienced in rocket launches and reentries. (credit: NASA) (b) Rider in cage showing how the cage pivots outward during rotation. This allows the total force exerted on the rider by the cage to be along its axis at all times.

  9. Integrated Concepts If a car takes a banked curve at less than the ideal speed, friction is needed to keep it from sliding toward the inside of the curve (a real problem on icy mountain roads). (a) Calculate the ideal speed to take a 100 m radius curve banked at 15.0º. (b) What is the minimum coefficient of friction needed for a frightened driver to take the same curve at 20.0 km/h?
  10. Modern roller coasters have vertical loops like the one shown in Figure 37.11. The radius of curvature is smaller at the top than on the sides so that the downward centripetal acceleration at the top will be greater than the acceleration due to gravity, keeping the passengers pressed firmly into their seats. What is the speed of the roller coaster at the top of the loop if the radius of curvature there is 15.0 m and the downward acceleration of the car is 1.50 g?
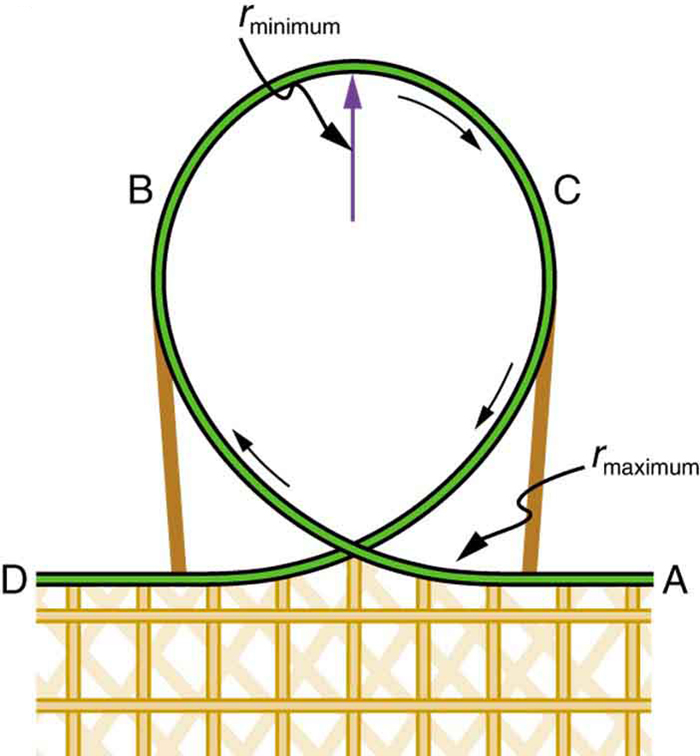
    A teardrop shaped loop of a roller coaster is shown. The car of the roller coaster starts from the point A near the right of the base and covers the teardrop portion of the roller coaster and move to a point D at the left of base. Near the top of tear drop portion an upward arrow is shown labeled as r-minimum. Also at a point near the base toward A there is a label called r-maximum. The wire frame of the base is also shown.
    Figure 37.11: Teardrop-shaped loops are used in the latest roller coasters so that the radius of curvature gradually decreases to a minimum at the top. This means that the centripetal acceleration builds from zero to a maximum at the top and gradually decreases again. A circular loop would cause a jolting change in acceleration at entry, a disadvantage discovered long ago in railroad curve design. With a small radius of curvature at the top, the centripetal acceleration can more easily be kept greater than [latex]g[/latex] so that the passengers do not lose contact with their seats nor do they need seat belts to keep them in place.
  11. Unreasonable Results (a) Calculate the minimum coefficient of friction needed for a car to negotiate an unbanked 50.0 m radius curve at 30.0 m/s. (b) What is unreasonable about the result? (c) Which premises are unreasonable or inconsistent?

Glossary

centripetal force
any net force causing uniform circular motion
ideal banking
the sloping of a curve in a road, where the angle of the slope allows the vehicle to negotiate the curve at a certain speed without the aid of friction between the tires and the road; the net external force on the vehicle equals the horizontal centripetal force in the absence of friction

ideal speed

the maximum safe speed at which a vehicle can turn on a curve without the aid of friction between the tire and the road
ideal angle
the angle at which a car can turn safely on a steep curve, which is in proportion to the ideal speed
banked curve
the curve in a road that is sloping in a manner that helps a vehicle negotiate the curve
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book