"

Kinematics

8 Displacement

Learning Objectives

  • Define position, displacement, distance, and distance traveled.
  • Explain the relationship between position and displacement.
  • Distinguish between displacement and distance traveled.
  • Calculate displacement and distance given initial position, final position, and the path between the two.

 

Three people cycling along a canal. The blurred buildings in the background convey a sense of motion of the cyclists.
Figure 7.1: These cyclists in Vietnam can be described by their position relative to nearby buildings and the canal. Their motion is described by their displacement—how far and in what direction they move relative to a defined frame of reference (credit: Suzan Black, Fotopedia)

Position: Where is the Object?

To describe motion scientifically, we first need to define position—where something is, relative to a known reference point or frame of reference.

  • In biology, we might describe the position of a tagged animal relative to its nest, or a migrating whale relative to the coast.

  • In a lab, you might describe the position of a moving sample under a microscope relative to the center of the viewing field.

Usually, we use Earth or a fixed point in a diagram as the reference frame. But sometimes the reference itself is moving, such as when we describe the motion of a person inside a moving train or insect walking on a leaf blowing in the wind.

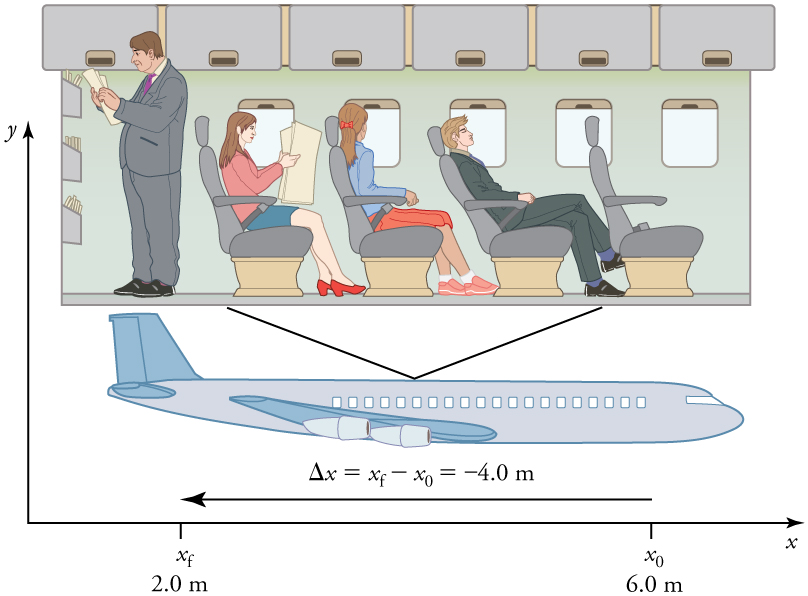
For example, a rocket launch would be described in terms of the position of the rocket with respect to the Earth as a whole, while a professor’s position could be described in terms of where she is in relation to the nearby white board. (See Figure 7.2.) In other cases, we use reference frames that are not stationary but are in motion relative to the Earth. To describe the position of a person in an airplane, for example, we use the airplane, not the Earth, as the reference frame. (See Figure 7.3.)

Displacement

When an object moves relative to that reference frame—whether it’s a bird in the sky, a researcher pacing in a lab, or a molecule inside a cell—we say the object has changed its position. This change in position is called displacement.

Displacement

Displacement is defined as:

[latex]\Delta x = x_f - x_0[/latex]

\Delta x = x_f – x_0where:

  • [latex]\Delta x[/latex] is the displacement,

  • [latex]x_f[/latex]is the final position,

  • [latex]x_0[/latex]is the initial position

 The Greek letter delta ([latex]\Delta x[/latex]) always means “change in.”

Displacement includes both magnitude and direction. It is a vector quantity, which means it can be positive or negative depending on the direction of motion. For example, if we define motion to the right (or east) as positive, then any motion to the left (or west) is considered negative.

SI Unit: The standard unit of displacement is the meter (m) (see Physical Quantities and Units).

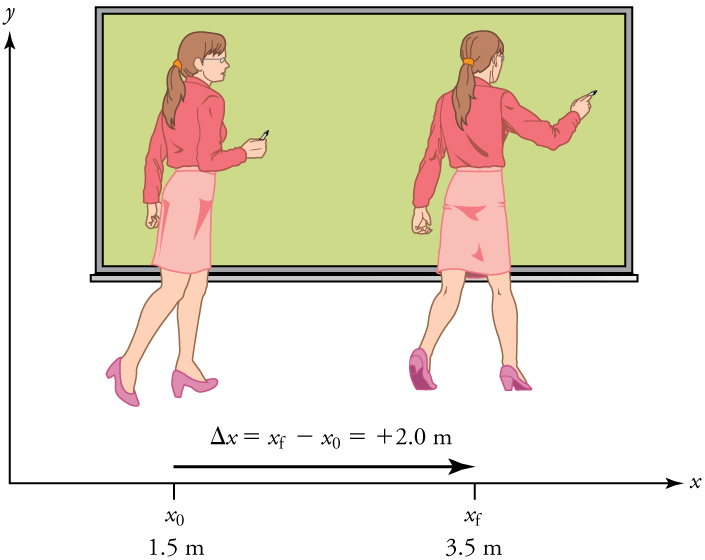
The initial and final position of a professor as she moves to the right while writing on a whiteboard. Her initial position is 1 point 5 meters. Her final position is 3 point 5 meters. Her displacement is given by the equation delta x equals x sub f minus x sub 0 equals 2 point 0 meters.
Figure 7.2: A professor pacing during a lecture changes position relative to the whiteboard. Her displacement is

+2.0m+2.0\text{ m}, shown by the rightward-pointing arrow.

View of an airplane with an inset of the passengers sitting inside. A passenger has just moved from his seat and is now standing in the back. His initial position was 6 point 0 meters. His final position is 2 point 0 meters. His displacement is given by the equation delta x equals x sub f minus x sub 0 equals 4 point zero meters.
Figure 7.3: A passenger walking toward the rear of an airplane has a displacement of -4.0m. The arrow points to the left, indicating negative displacement in the chosen frame of reference.

Note that displacement has a direction as well as a magnitude. The professor’s displacement is 2.0 m to the right, and the airline passenger’s displacement is 4.0 m toward the rear. In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually that will be to the right or up, but you are free to select positive as being any direction). The professor’s initial position is [latex]{x}_{0}=1\text{.}5\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] and her final position is [latex]{x}_{\text{f}}=3\text{.}5\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]. Thus her displacement is

[latex]\Delta x={x}_{f}-{x}_{0}=3\text{.5 m}-1.5 m=+2\text{.0 m}.[/latex]

In this coordinate system, motion to the right is positive, whereas motion to the left is negative. Similarly, the airplane passenger’s initial position is [latex]{x}_{0}=6\text{.}0 m[/latex] and his final position is [latex]{x}_{f}=2\text{.}0 m[/latex], so his displacement is

[latex]\Delta x={x}_{f}-{x}_{0}=2\text{.}0 m-6\text{.}0 m=-4\text{.}0 m.[/latex]

His displacement is negative because his motion is toward the rear of the plane, or in the negative [latex]x[/latex] direction in our coordinate system.

Distance

Displacement is different from distance. Displacement considers direction, but distance is scalar—it only has magnitude. It is the size of the total path traveled, regardless of direction.

For example:

  • If a professor walks back and forth across a 2 m stretch of classroom five times, her displacement might be 0 (if she returns to her starting point), but her distance traveled would be 10 m.

This distinction is especially important in fields like neuroscience (tracking neuron signal travel) or ecology (mapping animal migration), where understanding directional movement is different from path length.

Misconception Alert: Distance Traveled vs. Magnitude of Displacement

Don’t confuse the magnitude of displacement (just the number, without direction) with the total distance traveled. They are only the same if the motion is in a straight line and in a single direction. Otherwise, the total distance traveled is always greater than or equal to the magnitude of the displacement.

Check Your Understanding

A cyclist rides 3 km west and then turns around and rides 2 km east. (a) What is her displacement? (b) What distance does she ride? (c) What is the magnitude of her displacement?

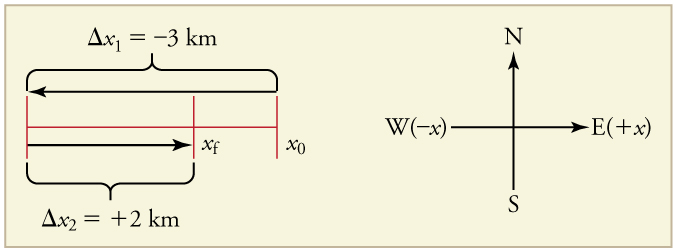
Two diagrams side by side. To the left is a horizontal line, or x axis, with points for final position and initial position. Displacement 1, shown by an arrow pointing leftward, equals negative 3 kilometers. Displacement 2, shown by an arrow pointing rightward, equals 2 kilometers. To the right is a pair of x and y axes, showing that east is the positive x direction and west is the negative x direction.
Figure 7.4
  1. The rider’s displacement is [latex]\Delta x={x}_{f}-{x}_{0}=\text{−1 km}[/latex]. (The displacement is negative because we take east to be positive and west to be negative.)
  2. The distance traveled is [latex]\text{3 km}+\text{2 km}=\text{5 km}[/latex].
  3. The magnitude of the displacement is [latex]1 km[/latex].

Section Summary

  • Kinematics is the study of motion without regard to its causes.

  • Displacement is the change in position and is defined as: [latex]\Delta x = x_f - x_0[/latex]

  • Displacement is a vector (includes direction); distance is a scalar (includes only magnitude).

  • Always define a positive direction at the start of a problem.

  • Distance traveled is the total path length, which may be greater than the magnitude of the displacement.

Conceptual Questions

  1. Give an example in which there are clear distinctions among distance traveled, displacement, and magnitude of displacement. Specifically identify each quantity in your example.
  2. Under what circumstances does distance traveled equal magnitude of displacement? What is the only case in which magnitude of displacement and displacement are exactly the same?
  3. Bacteria move back and forth by using their flagella (structures that look like little tails). Speeds of up to [latex]\text{50 μm/s}\phantom{\rule{0.25em}{0ex}}\left(\text{50}×{\text{10}}^{-6}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)[/latex] have been observed. The total distance traveled by a bacterium is large for its size, while its displacement is small. Why is this?

Problems & Exercises

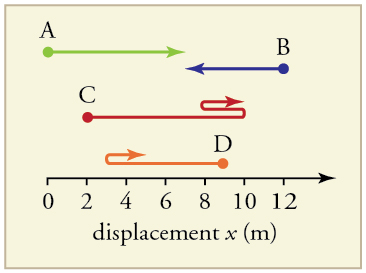
An x axis starts at 0 meters and ends at 12 meters. There are four points on the graph with displacement paths. Path A starts at 0 and stops at 7. Path B starts at 12 and ends at 7. Path C starts at 2, goes to 10, turns around and goes back to 8, then turns around again and stops at 11. Path D starts at 9, goes to 3, then turns around and stops at 5.
Figure 7.5

Refer to Figure 7.5 for the following exercises:

  1. Find the following for path A in Figure 7.5:
    1. The distance traveled.
    2. The magnitude of the displacement from start to finish.
    3. The displacement from start to finish.
  2. Find the following for path B in Figure 7.5:
    1. The distance traveled.
    2. The magnitude of the displacement from start to finish.
    3. The displacement from start to finish.
  3. Find the following for path C in Figure 7.5:
    1. The distance traveled.
    2. The magnitude of the displacement from start to finish.
    3. The displacement from start to finish.
  4. Find the following for path D in Figure 7.5:
    1. The distance traveled.
    2. The magnitude of the displacement from start to finish.
    3. The displacement from start to finish.

Glossary

kinematics
the study of motion without considering its causes
position
the location of an object at a particular time
displacement
the change in position of an object
distance
the magnitude of displacement between two positions
distance traveled
the total length of the path traveled between two positions
definition

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics 1 Copyright © 2012 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book