9 Reaction Systems
Melanie M. Cooper and Michael W. Klymkowsky

In the real world, simple chemical reaction systems are rare. Chemistry lab experiments typically involve mixing pure chemicals together in well-defined amounts under tightly-controlled conditions. In the wild, things are messier. There are usually a number of chemical species present, and this leads to competing reactions. Laboratory systems are effectively closed systems, and the results are analyzed only after the reaction has reached equilibrium. Real systems, on the other hand, are usually open and rarely reach equilibrium. This is particularly true for living systems, which tend to die if they reach equilibrium or become enclosed. In fact, most real systems are subject to frequent short- and long-term perturbations. We learned in the last chapter that perturbations (adding or taking away a product or a reactant) lead to compensatory changes and the system responds, as described by Le Chatelier’s principle. In the context of a more complex system, this simple behavior can produce quite dramatic results. Life is an example of such a system that has survived in its various forms uninterrupted for over 3.5 x 109 years.
In this chapter, we examine a range of complex systems and consider how living systems keep the concentration of important chemical species at a reasonable level (for example, by buffering the pH); how they use differences in concentrations of chemical species to drive cellular processes (like thought); and how reactions that release energy (by forming more stable compounds with stronger bonds) can be coupled to reactions that require energy in order to occur.
9.1 Systems Composed of One Reaction
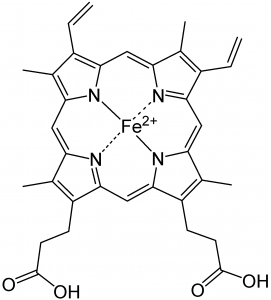 We begin with a few important reactions that can either move backward or forward depending on conditions.[1] Molecular oxygen (O2) is a vital component in a number of reactions in our bodies, such as aerobic respiration, the evolutionarily ancient process by which we capture energy from food.[2] O2 must be transported to every cell so that it can participate in cellular reactions. O2 diffuses into the bloodstream in the lungs, but it is not very soluble in water (the main component of blood). If we relied on the solubility of oxygen in water to transport it around the body, we would be in trouble. Instead O2 reacts with (we usually say “binds to”, but this is definitely a chemical reaction) a protein called hemoglobin. The structure of hemoglobin is complex: it is composed of four polypeptide subunits and each polypeptide is associated with a heme group.[3] The heme group contains an iron ion (Fe2+) complexed to four nitrogenous bases linked into a ring (called a porphyrin) to form a more or less planar arrangement, as shown in the figure. Heme is also the central active portion of one of the major components of our immune system, myeloperoxidase.[4]
We begin with a few important reactions that can either move backward or forward depending on conditions.[1] Molecular oxygen (O2) is a vital component in a number of reactions in our bodies, such as aerobic respiration, the evolutionarily ancient process by which we capture energy from food.[2] O2 must be transported to every cell so that it can participate in cellular reactions. O2 diffuses into the bloodstream in the lungs, but it is not very soluble in water (the main component of blood). If we relied on the solubility of oxygen in water to transport it around the body, we would be in trouble. Instead O2 reacts with (we usually say “binds to”, but this is definitely a chemical reaction) a protein called hemoglobin. The structure of hemoglobin is complex: it is composed of four polypeptide subunits and each polypeptide is associated with a heme group.[3] The heme group contains an iron ion (Fe2+) complexed to four nitrogenous bases linked into a ring (called a porphyrin) to form a more or less planar arrangement, as shown in the figure. Heme is also the central active portion of one of the major components of our immune system, myeloperoxidase.[4] 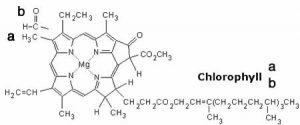 When you blow your nose, that familiar green color is actually caused by the light absorbing properties of the heme group in this enzyme, rather than the bacterial infection. Because the heme group is in a different molecular environment, its color appears green rather than red. Chlorophyll, a similar molecule, differs most dramatically from heme in that the iron ion is replaced by a magnesium ion (as shown in the figure). Its function is not to bind O2 (or CO2), but rather to absorb visible light and release an energetic electron as part of the photosynthetic process.
When you blow your nose, that familiar green color is actually caused by the light absorbing properties of the heme group in this enzyme, rather than the bacterial infection. Because the heme group is in a different molecular environment, its color appears green rather than red. Chlorophyll, a similar molecule, differs most dramatically from heme in that the iron ion is replaced by a magnesium ion (as shown in the figure). Its function is not to bind O2 (or CO2), but rather to absorb visible light and release an energetic electron as part of the photosynthetic process.
Iron is a transition metal. Recall that these elements have d orbitals, some of which are empty and available for bonding. Iron II (Fe2+) has plenty of energetically-available orbitals, and therefore can form Lewis acid–base complexes with compounds that have available electrons (such as nitrogenous bases). Within the porphyrin ring, four nitrogens interact with the Fe2+ ion. Typically, transition metals form complexes that are geometrically octahedral. In the case of the heme group, four of these interactions involve nitrogens from the four rings; a fifth involves a nitrogen of histidine residue of one of the protein’s polypeptides that approaches from below the ring plane. This leaves one site open for the binding of an O2 molecule, which has available lone electron pairs.[5] When an O2 binds to one of these heme groups,
Hemoglobin + O2 ⇄ Hemoglobin – O2.
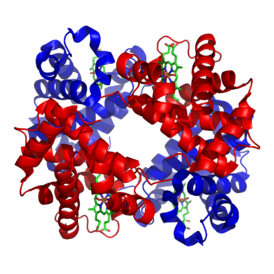 Note that this way of depicting the reaction is an oversimplification. As we said initially, each hemoglobin molecule contains four polypeptides, each of which is associated with a heme group (green in the figure), so there are four heme groups in a single hemoglobin molecule. Each heme group can bind one O2 molecule. When an O2 molecule binds to the heme iron, there are structural and electronic changes that take place within the protein as a whole. This leads to a process known as cooperativity, wherein the four heme groups do not act independently. Binding O2 to one of the four heme groups in hemoglobin causes structural changes to the protein, which increases the affinity for O2 in each of the remaining three heme groups. When a second O2 binds, affinity for O2 is once again increased in the remaining two heme groups.
Note that this way of depicting the reaction is an oversimplification. As we said initially, each hemoglobin molecule contains four polypeptides, each of which is associated with a heme group (green in the figure), so there are four heme groups in a single hemoglobin molecule. Each heme group can bind one O2 molecule. When an O2 molecule binds to the heme iron, there are structural and electronic changes that take place within the protein as a whole. This leads to a process known as cooperativity, wherein the four heme groups do not act independently. Binding O2 to one of the four heme groups in hemoglobin causes structural changes to the protein, which increases the affinity for O2 in each of the remaining three heme groups. When a second O2 binds, affinity for O2 is once again increased in the remaining two heme groups.
As you might suspect, this process is reversible. Imagine a hemoglobin protein with four bound oxygen molecules. When an O2 is released from the hemoglobin molecule, the affinity between the remaining O2s and the heme groups is reduced, making it more likely that more of the bound O2s will be released. This is an equilibrium reaction, and we can apply Le Chatelier’s principle to it. Where O2 is in abundance (in the lungs), the reaction shifts to the right (binding and increasing affinity for O2). Where O2 is present at low levels, the reaction shifts to the left (releasing and reducing affinity for O2). The resulting hemoglobin molecule has a high capacity for binding O2 where O2 is present at high concentrations and readily releases O2 where O2 is present at low concentrations. In the blood, [hemoglobin] ranges between 135–170 g/L, approximately 2 millimoles per liter (mM), and because there are four O2 binding sites per hemoglobin, this results in approximately ~ 250 mg/L or s8-mM concentration of O2.
By comparison, O2‘s solubility in water is ~ 8mg/L at 37 ºC, or 250 micromoles per liter (μM). The reaction can be written like this:
O2 in the air ⇄ O2 in the blood (liquid) + hemoglobin ⇄ hemoglobin-O2 + O2 in the blood ⇌ hemoglobin-2O2 + O2 in the blood ⇄ hemoglobin-3O2 + O2 in the blood ⇄ hemoglobin-4O2
When the hemoglobin reaches areas of the body where [O2] is low, the oxygen dissociates from the hemoglobin into the blood. The dissolved O2 is then removed from the blood by aerobic (oxygen-utilizing) respiration: C6H12O6 + 6O2 ⇄ 6CO2 + 6H2O.
The combination of Le Chatelier’s principle and the cooperativity of the O2 + hemoglobin reaction now leads to the complete dissociation of the hemoglobin—4O2 complex, releasing O2. The products of aerobic respiration (essentially a combustion reaction) are carbon dioxide and water. Clearly the water can be carried away in cellular fluid, but the carbon dioxide must be removed in a variety of ways: a small part is removed by reacting with the hemoglobin (but not at the Fe center), some is dissolved in the blood, and some takes part in the buffering system present in the blood, and most is released in the lungs, into the air that you breath out.
Questions
Questions to Answer
- What complicates reaction systems in the real world (outside the lab)?
- Why is O2 not very soluble in water?
- By what factor does binding with hemoglobin increase solubility of O2 in water?
- Draw Lewis structures for O2 and CO. Why do you think they bind in similar ways to hemoglobin?
- Why does CO2 react differently with hemoglobin from the way O2 interacts with hemoglobin?
Questions to Ponder
- Why does it make physiological sense that O2 binds to oxygen-free hemoglobin (deoxyhemoglobin) relatively weakly and cooperatively ?
9.2 Buffered Systems
When you think of the word buffer, you probably think of it as a safeguard or a barrier—something that provides a cushion or shield between you and something harmful. But in chemistry and biology, a buffer is a solution that resists changes in pH. As we will soon learn, this ability is critical to all living systems. Many reactions are affected by changes in pH. For example, strong acid and base solutions are harmful to living tissue because they cause rapid hydrolysis of the bonds that hold living organisms together. That is, acidic or basic solutions can speed up the reactions in which the bonds are broken (dead bodies are often disposed of in murder mysteries—and sometimes in real life—by dissolving them in strong acid or base). Proteins have many weak acid and base groups, and so even relatively small fluctuations in pH can cause changes in the charges of these groups. This can affect protein structure and function dramatically, in a way that is physiologically damaging to living systems.
Aqueous solution chemistry is terrifically complicated in living systems. However, we can begin to understand it by looking at simple chemical buffer systems. Let us first consider what happens if we take 0.10 moles of hydrogen chloride gas and dissolve it in enough water to make one liter of solution. The resulting 0.10-M solution of hydrochloric acid HCl (aq) has a pH of 1 (pH = – log (0.10), = – log (1.0 x 10–1). So the pH of the solution changes from 7 (for pure water) to 1, a change of 6 orders of magnitude in [H+]. Now, if we do the same experiment adding 0.10 mol HCl(g) to an appropriately buffered solution, we find the pH of the resulting solution does not change very much at all.
To understand how this happens, we have to review some acid–base chemistry. Specifically, we must reexamine what happens when acids and base react, what the products are, and how those products behave. We just calculated that the pH of a 0.10-M strong acid is 1.0. It does not matter which strong acid we choose, as long as it only has one proton to donate. So the pH of solutions HCl, HBr, and HClO4 are all the same because they are all almost completely ionized in aqueous solution. However, what happens if we use a weak acid like acetic acid (CH3COOH), hydrogen fluoride (HF), phosphoric acid (H3PO4), or carbonic acid (H2CO3)? The pH of each differs and none of them is as low as the strong acids because they do not ionize completely in solution. For example, the pH of 0.10-M acetic acid is ~2.9 because the concentration of H+ is lower than in 0.10-M HCl. Although that may not seem very different from a pH of 1, remember that [H+] is 10-1 (or 0.1 M) for a pH of 1 and 10-2.9 (or 0.0012 M) for a pH 2.9.
Now if we look at the conjugate bases of weak and strong acids we will see an analogous difference in their behavior to produce solutions with different pHs. The conjugate base of HCl is Cl– (the chloride ion.) However since we can’t just get a bottle of chloride (we need a counter ion for charge balance), we will use sodium chloride, NaCl, since we know that sodium ions are not reactive, they are usually “spectator” ions. If we measure the pH of a solution of NaCl, we will find that it is 7, just like water. Neither the sodium ion nor the chloride ion affects the pH. However, if we take the corresponding conjugate base from acetic acid, for example sodium acetate (CH3COONa), we find that a 0.1 M solution has a pH of about 9. This is quite surprising at first glance. Sodium acetate belongs to the class of compounds that we label generically as salts. In everyday life, salt refers to sodium chloride, but in chemistry the term salt refers to a compound that contains the conjugate base of an acid and a cation. Although it is tempting to think of all salts as innocuous and unreactive (like sodium chloride), it turns out that components of the salt (the conjugate base anion, and the cation) both affect the properties, even in a simple reaction like dissolving in water. In fact, the pH of any conjugate base of a weak acid tends to be basic.
Let us investigate a bit further. The previous observation implies that the acetate ion (CH3COO–) must be reacting with water to produce hydroxide (since we already know the Na+ does not react with water). This reaction is called a hydrolysis reaction. The name is derived from the Greek words for water (hydro-) and to break or separate (-lysis); it refers to reactions in which water is one of the reactants. We can write this hydrolysis reaction as:
CH3COO–(aq) + H2O(l) ⇄ CH3COOH(aq) + –OH(aq)
The production of hydroxide increases [–OH], in turn affects [H+] because the two are related by the equilibrium expression [H+] [–OH] = 1 x 10–14 = Kw. In other words, when the salt of a weak acid (that is, its conjugate base) is dissolved in water, a weak base is produced and that weak base has all the properties of any base: it can react with an acid.
It is possible to calculate the pH of weak base solutions, just as it is to calculate the pH of weak acids, if you know the acid equilibrium constant.[6] However, what is more interesting is what happens when a solution contains significant amounts of both a weak acid and its conjugate base. For example, if we take a solution that is 0.10 M in both acetic acid and sodium acetate, we can calculate the pH by setting up the equilibrium table:
| AcOH | + H2O | ⇌ H3O+ | + –OAc | + Na+ |
| Initial concentrations 0.10 M | 1 x 10–7 | 0.10 M | 0.10 M |
Note that even though acetate is present in the initial mixture, we have put it on the product side. This is because when both acetic acid and acetate are present in the same solution, their concentrations are “linked”: they become part of an equilibrium system that can be described by the equilibrium constant for acetic acid.[7] If the concentration of one species is changed, the other must respond. Recall in Chapter 8 that we looked at what happens to the pH of a solution of acetic acid when an acetate ion is added: the presence of acetate affects the position of equilibrium for the acetic acid dissociation, and instead of a pH of 2.9 (for 0.10 M acetic acid), the pH of a solution that is 0.10 M in both acetic acid and sodium acetate is 4.7. The presence of the common ion acetate has suppressed the ionization of acetic acid. We can calculate the pH of any similar solution by adapting the expression for the acid dissociation equilibrium:
Ka = [H+][AcO–]/[AcOH].
As in our previous work with weak acids we are going to ignore any reaction with water from both the acetic acid and the acetate ion because they do not affect the pH significantly; both species are relatively weak as acids or bases. Even if we take these reactions into account, they do not change the answer we get. Substituting in the equation for Ka, we get:
Ka = 1.8 x 10–5 = [H+] (0.10)/(0.10).
Alternatively, we can use pKa, the negative log of Ka, giving us:
pKa = pH – log [AcO–]/[AcOH]
or pH = pKa + log [AcO–]/[AcOH].
This equation is known as the Henderson–Hasselbalch equation. It is a convenient way to calculate the pH of solutions that contain weak acids and their conjugate bases (or weak bases and their conjugate acids).
Recall that a buffer can resist changes in pH. So the question is: how exactly does this happen? Let us take a closer look. Imagine we have a buffer solution that is 1.0 M in both acetic acid and acetate. The pH of this system is –log 1.8 x 10–5 = 4.74 (because [AcO–] = [AcOH]). Now let us add some acid to this buffer. To make calculations easy, we can add 0.01 mol HCl to 1.0 L of buffer solution.[8] What happens? The major species in the buffer solution are acetic acid, acetate, and water (hydronium ion and hydroxide ion are minor components). Which one will react with HCl(aq)? Just as in any acid–base reaction, it is more likely that the base will react with the acid that is, the acetate part of the buffer will react with the H+. The resulting reaction is:
H+ + –OAc ⇄ AcOH + H2O.
In this reaction, the acetate concentration decreases and the acetic acid increases. We can now calculate the initial (pre-reaction) and final (post-reaction) concentrations:
| AcOH | + H2O | ⇄ H3O+ | + –OAc | |
| Initial [M] | 1.00 | (negligible) | 1.00 | |
| add 0.01 M H++ | +0.01 | – 0.01 | ||
| Equilibrium [M] | 1.01 | x | 0.99 |
The pH of this system can be calculated from the Henderson–Hasselbalch equation:
pH = pKa + log (0.99/1.01) = 4.73.
The pH has hardly budged! (Recall that the pH of 0.01 M HCl is 2.0.) Even if we add more acid (say, 0.1 mol HCl) to our liter of buffer, the resulting pH does not change much (it is pH = 4.74 + log (0.90/1.10) = 4.65). Note that the addition of acid has moved the pH in the direction we would expect—slightly lower and more acidic but nowhere near what it would be if we had added the HCl directly to 1 L of water.
We can also look at what happens when we add a strong base to the buffer solution. If we add 0.01 mol sodium hydroxide to our liter of buffer, the “active” component of the buffer is now the acid, and the reaction is written: HOAc + –OH ⇄ AcO– + H2O.
The strong base reacts with the weak acid. The acid concentration falls and its conjugate base concentration rises, so:
| AcOH | + H2O | ⇄ H3O+ | + –OAc | |
| Initial [M] | 1.00 | (negligible) | 1.00 | |
| add 0.01 M –OH | -0.01 | + 0.01 | ||
| Equilibrium [M] | 0.99 | x | 1.01 |
The new pH of the solution is pH = 4.74 + log (1.01/0.99) = 4.75—a slight increase but hardly detectable. (Note that the pH of a 0.01 M solution of NaOH is 12.)
So, buffers can keep the pH of a solution remarkably constant. – which, as we will see, this is very important for biological systems. But this raises another question, just how much acid could we add to the system before the pH did change appreciably, or rather, enough to influence the behavior of the system? In biological systems, the tolerance for pH change is fairly low. As we discussed previously, changes in pH can cause a cascade of reactions that may prove catastrophic for the organism.
The amount of acid or base that a buffer solution can absorb is called its buffering capacity. This capacity depends on the original concentrations of conjugate acid and base in the buffer and their ratio after reaction, or [conjugate acid]/[conjugate base]. If you start with a buffer that has equal amounts of acid and base, the ratio is equal to 1.0. As the ratio moves further away from 1.0, the pH is affected more and more, until it changes out of the desired range.
Another important property of buffers is the range of pH that they can act over. As we have seen from the Henderson–Hasselbalch equation, when the concentration of acid is equal to the concentration of base, the pH of the solution is equal to the pKa of the acid. Thus, the acetic acid/acetate buffer has a pH = 4.74. Generally, the effective buffering range is +1 or –1 pH unit around the pKa. So the acetic acid/acetate acts as an effective buffer in the range of pH 3.7-5.7, well within the acidic pH region. There are biological compartments (the stomach, lysosomes, and endosomes) that are acidic but the major biological fluids (cytoplasm and blood plasma) have pHs around 7.2–7.4. In these systems, buffers are phosphate or carbonate systems. For example, the phosphate buffer system is composed mainly of H2PO4– (the proton donor or acid), and HPO42– (the proton acceptor or base): H2PO4– + H2O ⇄ HPO42– + H3O+
What counts as an acid or a base depends entirely on the reaction system you are studying. This is an important point. Both H2PO4– and HPO42– can act as either an acid or a base depending on the pH. (Try writing out the reactions.) But at physiological pH (7.2-7.4), the predominant forms are H2PO4– and HPO42–. The pKa of the conjugate acid is 6.86 so it makes sense that this buffer system is active in cellular fluids.
Questions
Questions to Answer
- How much acid would you have to add to change the pH of a buffer that is 1.0 M in acid and conjugate base by one full pH unit?
- If the buffer is 0.1 M in acid and conjugate base, would you have to add the same amount of acid? Why or why not?
- What buffer systems would you use to buffer a pH of 4, 6, 8, and 10? What factors would you take into account?
- Carbonic acid (H2CO3) has two acidic protons. Draw out the structure of carbonic acid, and show how each proton can take part in an acid–base reaction with a strong base such as sodium hydroxide.
- What is the pH of a buffer system if the concentration of the acid component is equal to the concentration of its conjugate base?
- Can any buffer system buffer any pH? For example, could an acetic acid/acetate system effectively buffer a pH of 9?
- What criteria would you use to pick a buffer system for a particular pH?
Questions to Ponder
- What factors might make reactions sensitive to pH?
- Why are protein structure and activity sensitive to changes in pH?
- Which parts of proteins are affected by changes in pH? What kinds of chemical properties must they have? What groups of atoms do these bits of proteins contain?
- Would you expect nucleic acids to be more or less sensitive to pH changes than proteins?
9.3 Amino Acids, Proteins, and pH
In addition to examining how adding a strong acid or base affects a buffer solution, we can also look at the effect of pH on a particular acid or base. This is particularly important in biological systems where there are many weak acid or base groups that can be affected by the pH. For example, proteins contain both weakly acidic –COOH and weakly basic –NH2 groups. A 1.0-M solution of a simple carboxylic acid like acetic acid has a pH of ~ 2.8; it turns out that most carboxylic acids behave in a similar way. If we manipulate the pH, for example, by adding a strong base, the acetic acid reacts with the base to form an acetate ion. Based on the Henderson–Hasselbalch equation, when [acetate] = [acetic acid], the pH equals the acid’s pKa, which is 4.74. As the pH increases, the concentration of acetate must also increase, until by pH ~7 (approximately normal physiological pH). At this point the concentration of acetic acid is very small indeed. The ratio of base to acid is about 200/1. That is, at physiological pHs groups such as carboxylic acids are deprotonated and exist in the carboxylate (negatively charged) form.
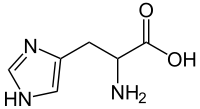
Conversely, if we look at the amino group (–NH2) of a protein, it is actually the base part of a conjugate acid-base pair in which the acid is the protonated form –NH3+. The pKa of an –NH3+ group is typically ~9. At a pH of 9 there are equal amounts of the protonated (– NH2) and unprotonated forms (–NH3+). So if we change the pH by adding an acid, the concentration of –NH3+ form increases as the base form –NH2 is protonated. At pH ~7 there is little of the –NH2 form remaining. Interestingly, this means that an amino acid (shown in the figure) never exists in a state where both the amino (–NH2) group and the carboxylic acid (–CO2H) exist at the same time. The “neutral” species is in fact the one in which –NH3+/–CO2– are present. This zwitterion (that is a neutral molecules with a positive and negative electrical charge at different locations, from the German zwitter, meaning “between”) is the predominant form at physiological pH.
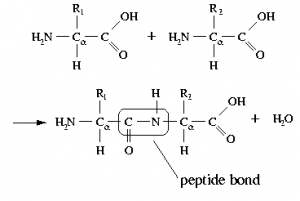
A protein is composed mainly (sometimes solely) of polymers of amino acids, known as polypeptides. In a polypeptide, the amino (–NH2) and carboxylic acid (–CO2H) groups of amino acids are bonded together to form a peptide bond (see figure). The resulting amide group (peptide bond) is neither acidic nor basic under physiological conditions.[9] That being said, many of the amino acids found in proteins have acidic (aspartic acid or glutamic acid) or basic (lysine, arginine, or histidine) side chains. The pH of the environment influences the conformations of the protein molecule and the interactions between these charged side chains (the spontaneous native conformations of the molecule are called protein folding). Changes from the “normal” environment can lead to changes in protein structure, and this in turn can change biological activity. In some cases, protein activity is regulated by environmental pH. In other cases, changes in pH can lead to protein misfolding (or denaturation, which in living organisms can cause disruption of cell activity or death). For example, if these groups are protonated or deprotonated, the electronic environment in that region of the protein can change drastically, which may mean that the protein will not only change how it interacts with other species but its shape may change so as to minimize repulsive interactions or produce new attractive interactions. Small changes in protein shape can have profound effects on how the protein interacts with other molecules and, if it is a catalyst, its efficiency and specificity. In fact, there are cases where environmental pH is used to regulate protein activity.
Questions
Questions to answer:
- What would be the ratio of –NH3+/–NH2 in a solution of a protein at pH 5, pH 7, and pH 9?
- What kinds of interactions would each form participate in?
- What is the predominant form of a carboxylic acid group at pH 5? pH 7, pH 9
- What kinds of interactions would each form participate in?
- What is the ratio of –NH3+/–NH2 in a solution of a protein at pH 5, pH 7, and pH 9? What kinds of interactions does each form participate in?
- What is the predominant form of a carboxylic acid group at pH 5? How about at pH 7 and pH 9? What kinds of interactions does each form participate in?
9.4 Coupled, Non-Equilibrium Reaction Systems
Another important buffer system is the carbonic acid (H2CO3) bicarbonate (HCO3–) buffer, which is a major buffering component of blood plasma. This system is more complex than the phosphate buffer, because carbonic acid is formed by the reversible reaction of carbon dioxide in water:
H2O + CO2 ⇄ H2CO3 and H2CO3 + H2O ⇄ HCO3– + H3O+
These are two reactions linked (or coupled) by a common intermediate. By examining these reactions more closely, we see how some systems exist under non-equilibrium conditions and how some reactions occur despite the fact that they have a positive free energy change and appear to contravene the second law of thermodynamics.
As we have seen previously, simple chemical reactions are characterized by how fast they occur (their rate) and how far they proceed toward equilibrium. While you will learn much more about reactions if you continue on in chemistry, that is not something we will pursue here – rather we will consider the behavior of systems of reactions and their behavior, particularly when they have not reached equilibrium. This is a situation common in open systems, systems in which energy and matter are flowing in and out. In Chapter 8, we considered single reactions and what happens when we perturb them, either by adding or taking away matter (reactants or products) or energy (heating or cooling the reaction.) Now it is time to look at what happens when reactions are coupled: when the products of one reaction are the starting materials for other reactions occurring in the same system.
Take for example the coupled system introduced above – the pair of reactions that are linked by the formation and reaction of carbonic acid.
H2O + CO2 ⇄ H2CO3 and H2CO3 + H2O ⇄ HCO3– + H3O+
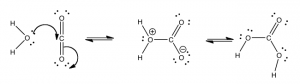
These coupled reactions are important for a number of reasons: they are responsible for the transport of excess carbon dioxide to the lungs and for buffering the pH of blood. Carbon dioxide enters the blood stream by dissolving in the plasma. However, it can also react with water in a reaction where the water acts as a nucleophile and the carbon dioxide acts an electrophile.
The formation of carbonic acid is thermodynamically unfavorable. The equilibrium constant for hydration of carbon dioxide is 1.7 x 10–3 and the standard free energy change ΔGº for the reaction[10] is 16.4 kJ. This means that the amount of carbonic acid in blood plasma is quite low; most carbon dioxide is just dissolved in the plasma (rather than reacted with the water). However, as soon as carbonic acid is formed, it can react with water:
H2CO3 + H2O ⇄ HCO3– + H3O+
to produce bicarbonate (HCO3–). Note that we now have the components of a buffer system (a weak acid, carbonic acid, and its conjugate base bicarbonate). The rate of this reaction is increased by the enzymatic catalyst carbonic anhydrase. In this buffer system the carbonic acid can react with any base that enters the bloodstream, and the bicarbonate with any acid. This buffering system is more complex than the isolated ones we considered earlier, because one of the components (carbonic acid) is also part of another equilibrium reaction. In essence, this means that the pH of the blood is dependent on the amount of carbon dioxide in the bloodstream:
H2O + CO2 ⇄ H2CO3 + H2O ⇄ HCO3– + H3O+
If we remove water from the equations (for the sake of clarity) we can see the connection better:
CO2 ⇄ H2CO3 ⇄ HCO3– + H3O+
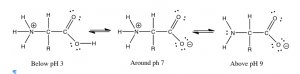
The pKa of carbonic acid is 6.37 and the pH of blood is typically 7.2–7.4, which does fall just within the buffering range. Under normal circumstances, this buffer system can handle most changes. However, for larger changes, other systems are called into play to help regulate the pH. For example, if you exert yourself, one of the products generated is lactic acid, (which we denote as LacOH).[11] When lactic acid finds its way into the bloodstream, it lowers the pH (increasing the amount of H3O+) through the reaction:
LacOH + H2O ⇄ H3O+ + LacO–
If we use Le Chatelier’s principle, you can see that increasing the H3O+ shifts the equilibrium toward the production of carbon dioxide in the buffer system. As the concentration of CO2 increases, a process known as chemoreception activates nervous systems, which in turn regulate (increase) heart and respiratory rates,which in turn lead to an increase in the rate of CO2 and oxygen exchange in the lungs.[12] As you breathe in O2, you breathe out CO2 (removing it from your blood). In essence, Le Chatelier’s principle explains why we pant when we exercise![13] Conversely, when some people get excited, they breathe too fast (hyperventilate); too much CO2 is removed from the blood, which reduces the H3O+ concentration and increases the pH. This can lead to fainting (which slows down the breathing), a rather drastic way to return your blood to its correct pH. An alternative, non-fainting approach is to breathe into a closed container. By breathing expelled CO2 (and a lower level of O2), you increase your blood pH.
While we can use Le Chatelier’s principle to explain the effect of rapid or slow breathing, this response is one based on what are known as adaptive and homeostatic systems. Biological systems are characterized by many such interconnected regulatory mechanisms. They maintain a stable, internal chemical environment essential for life. Coupled regulatory systems lie at the heart of immune and nervous system function. Understanding the behavior of coupled regulatory systems is at the forefront of many research areas, such as: measuring the physiological response to levels of various chemicals (chemoreception); recognizing and responding to foreign molecules in the immune system; and measuring the response to both external stimuli (light, sound, smell, touch) and internal factors (such as the nervous system). Downstream of the sensory systems examined by such efforts are networks of genes, proteins, and other molecules whose interactions are determined by the thermodynamics of the chemical system. Although they were formed by evolutionary processes, and are often baroque in their details, they are understandable in terms of molecular interactions, chemical reactions, and their accompanying energy changes.
Questions
Questions to Answer
- If the pKa of carbonic acid is 6.35 and the pH of blood is over 7, what do you think the relative amounts of carbonic acid and bicarbonate are? Why?
- Draw out the series of reactions that occur when lactic acid is introduced into the blood stream and explain why this affects the concentration of carbon dioxide in the blood stream.
- If the amount of carbon dioxide in the atmosphere increases, what effect does it have on oceans and lakes?
- If carbon dioxide dissolves in water to give carbonic acid, what do you think nitrogen dioxide (NO2) gives when dissolved in water? How about sulfur dioxide? What effect does this have on the pH of the water it dissolves in?
9.5 Energetics and Coupling
We have seen that for systems of coupled reactions, changing the concentration of one of the components in the system affects all the other components, even if they are not directly reacting with the one that is changed. We can use the same principles to explain why it is possible to carry out reactions that are thermodynamically unfavorable. We will consider a fairly simple example and then move on to see how this works in biological systems.
Many metals are not found in their elemental form. For example, copper—an important metal used for a wide range of applications from wires to roofs—is often found as chalcocite, an ore containing copper as copper sulfide. We can imagine a simple chemical reaction to separate the copper from the sulfide:[14]
Cu2S(s) ⇄ 2Cu(s) + S(s) ΔGº = 86.2 kJ/mol
Note that this reaction is a redox reaction in which the Cu+ ion is reduced to Cu by the addition of an electron (from the sulfide S2–, which is oxidized to sulfur with an oxidation state of 0.) Unfortunately, because the free energy change for this reaction is positive, the system at equilibrium is composed mostly of Cu2S(s). How can we get copper out of copper sulfide? One possibility to exploit the reaction between sulfur and oxygen:
S(s) + O2(g) ⇄ SO2 (g), for which ΔGº = –300.1 kJ/mol.
This reaction is highly favorable and “goes” toward the production of SO2. It is basically the burning of sulfur (analogous to the burning of carbon) and is another redox reaction in which the sulfur is oxidized (from an oxidation state of 0 to +4). Note that one reason why this reaction is so favorable is the formation of the strong S-O bonds, which is a highly exothermic process.
If we take Cu2S(s) together with O2(g), we have a system composed of two reactions:
Cu2S(s) ⇄ 2Cu(s) + S(s) [reaction 1]
S(s) + O2(g) ⇄ SO2 (g) [reaction 2]
These two reactions share a common component (S(s)); therefore, they are coupled. Imagine what happens when reaction 1 proceeds, even a little. The S(s) produced can then react with the O2(g) present. As this reaction proceeds toward completion, S(s) is removed, leaving Cu (s) and SO2 (g). Based on Le Chatelier’s principle, reaction 1 is now out of equilibrium, and thus generates more S(s) and Cu(s). Reaction 1 in isolation produces relatively little copper or sulfur, but it is dragged toward the products by reaction 2, a favorable reaction that removes sulfur from the system. If we assume that there are no other reactions occurring within the system, we can calculate the ΔGº for the coupled reactions 1 and 2. Under standard conditions, we simply add the reactions together:
| Cu2S(s) ⇆ 2Cu(s) + S(s) | 86.2 kJ/mol |
| S(s) + O2(g) ⇆ SO2 (g) | –300.1 kJ/mol |
| Cu2S(s) + O2(g) ⇆ 2Cu(s) + SO2 (g) | –213.9 kJ/mol |
So, the ΔGº for the coupled reaction is -213.9kJ/mol. This same basic logic applies to any coupled reaction system. Note that the common intermediate linking these two reactions is sulfur (S). However, it is not always so simple to identify the common intermediate. In this system, we are tacitly assuming that O2 and SO2 do not react with either Cu2S or SO2. If they did, those reactions would also need to be considered in our analysis. In fact, we need to consider all of the reactions that are possible with a system. This is normally not a big issue with simple chemical systems that contain relatively small numbers of different types of molecules (sometimes called species), but it is a significant concern when we consider biological or ecological systems that contain thousands of different types of molecules, which can interact and react in a number of ways.
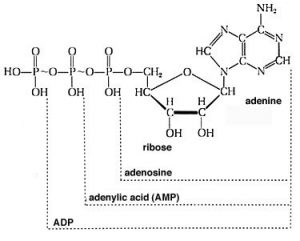 For example, you may have learned in biology that the molecule adenosine triphosphate (ATP) is used to store and provide energy for cellular processes. What exactly does this mean? First, let us look at the structure of ATP: it is composed of a base called adenine, a sugar ribose, and three phosphate units. For our purposes, the adenine base and sugar (called adenosine when attached to each other) are irrelevant. They do not change during most of the reactions in which ATP takes part. They are organic “building blocks” with functional groups that allow them to interact with other components in the cell for other functions (for example, in RNA and DNA). To examine energy transfer, we can just use “A” (adenosine) to stand in for their structure. The important bit for our purposes are the phosphates hooked together by the P—O—P (phosphoanhydride) linkages. At physiological pH, most (if not all) of the oxygens of the phosphate esters are deprotonated. This means that there is a fairly high concentration of charge in this tri-ester side chain, which acts to destabilize it. The bonds holding it together are relatively weak, and the molecule reacts with any available entity to relieve some of this strain and form even more stable bonds. For example, ATP is unstable in water and reacts (hydrolyzes) to form adenosine diphosphate (ADP) and inorganic phosphate (HPO4), which is often written as Pi. This reaction is written as ATP + H2O ⇄ ADP + Pi.
For example, you may have learned in biology that the molecule adenosine triphosphate (ATP) is used to store and provide energy for cellular processes. What exactly does this mean? First, let us look at the structure of ATP: it is composed of a base called adenine, a sugar ribose, and three phosphate units. For our purposes, the adenine base and sugar (called adenosine when attached to each other) are irrelevant. They do not change during most of the reactions in which ATP takes part. They are organic “building blocks” with functional groups that allow them to interact with other components in the cell for other functions (for example, in RNA and DNA). To examine energy transfer, we can just use “A” (adenosine) to stand in for their structure. The important bit for our purposes are the phosphates hooked together by the P—O—P (phosphoanhydride) linkages. At physiological pH, most (if not all) of the oxygens of the phosphate esters are deprotonated. This means that there is a fairly high concentration of charge in this tri-ester side chain, which acts to destabilize it. The bonds holding it together are relatively weak, and the molecule reacts with any available entity to relieve some of this strain and form even more stable bonds. For example, ATP is unstable in water and reacts (hydrolyzes) to form adenosine diphosphate (ADP) and inorganic phosphate (HPO4), which is often written as Pi. This reaction is written as ATP + H2O ⇄ ADP + Pi.
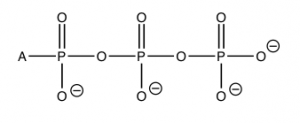 The standard free energy change for this reaction ΔGº = – 29 kJ/mol (at pH 7). This is a highly exergonic (heat or energy releasing) reaction; both the enthalpy and entropy changes for this reaction are favorable. ΔH is negative and ΔS is positive. It makes sense that the entropy change is positive. After all, we are producing two molecules from one. The enthalpy change also makes sense. We have already mentioned that ATP is unstable, and the loss of one of the phosphate groups relieves some of the strain caused by the charge repulsion between the three negatively charged phosphate groups in ATP. The bond energies in the product are stronger than the bond energies in the reactants and thus the reaction is exothermic. Like everything in living systems, this is all somewhat complicated by the presence of other substances in the cellular fluids, such as the metal ions Ca2+ and Mg2+, and changes in pH. However, the explanation is still valid. Make sure that you do not fall prey to the commonly held misconception that it is the breaking of the P—O bond that releases energy. On the contrary—it is the formation of more stable (stronger) bonds that releases energy.
The standard free energy change for this reaction ΔGº = – 29 kJ/mol (at pH 7). This is a highly exergonic (heat or energy releasing) reaction; both the enthalpy and entropy changes for this reaction are favorable. ΔH is negative and ΔS is positive. It makes sense that the entropy change is positive. After all, we are producing two molecules from one. The enthalpy change also makes sense. We have already mentioned that ATP is unstable, and the loss of one of the phosphate groups relieves some of the strain caused by the charge repulsion between the three negatively charged phosphate groups in ATP. The bond energies in the product are stronger than the bond energies in the reactants and thus the reaction is exothermic. Like everything in living systems, this is all somewhat complicated by the presence of other substances in the cellular fluids, such as the metal ions Ca2+ and Mg2+, and changes in pH. However, the explanation is still valid. Make sure that you do not fall prey to the commonly held misconception that it is the breaking of the P—O bond that releases energy. On the contrary—it is the formation of more stable (stronger) bonds that releases energy.
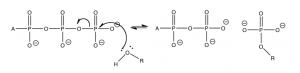
If we go one step further and look at the actual free energy change ΔG (as opposed to the standard change), using typical cellular concentrations of ATP, ADP and Pi, and ΔG = ΔGº + RTlnQ (where Q = [ADP][Pi]/[ATP]), we can calculate: ΔG = – 52 kJ/mol, assuming that the concentration of ATP is typically about ten times that of ADP, and that [Pi] is about 0.001 M. So in real conditions in the cell, the Gibbs free energy change is much higher than the standard Gibbs free energy change. This energy is not wasted; it is used to drive other reactions that would not otherwise occur. However, this energy cannot be used to drive just any random reaction. The reactions have to be coupled by common intermediates (just like the carbon dioxide carbonate system).
A typical reaction scenario is the transfer of the terminal phosphate group to another biomolecule as shown in the diagram. This transfer occurs with lipids and proteins, but typically the reacting group is an alcohol (ROH) or sometimes a carboxylic acid (RCOOH). The reaction that takes place is almost the same as the hydrolysis reaction except that the incoming nucleophile has much more “stuff” attached to the oxygen.
 The formation of these phosphate esters makes the original functional group more reactive. For example, the formation of an amide bond (the major bond that holds proteins together) is normally exergonic (about + 2 to 4 kJ/mol). The formation of amide bonds is not spontaneous (you might want to think about what this means for the amide bonds in the proteins that make up a good portion of you). Therefore, protein synthesis is coupled with ATP hydrolysis, as is the production of many biomolecules, sugars, lipids, RNA, and DNA. The reactions are complex, but each of them is driven by a series of individual reactions linked by common intermediates.
The formation of these phosphate esters makes the original functional group more reactive. For example, the formation of an amide bond (the major bond that holds proteins together) is normally exergonic (about + 2 to 4 kJ/mol). The formation of amide bonds is not spontaneous (you might want to think about what this means for the amide bonds in the proteins that make up a good portion of you). Therefore, protein synthesis is coupled with ATP hydrolysis, as is the production of many biomolecules, sugars, lipids, RNA, and DNA. The reactions are complex, but each of them is driven by a series of individual reactions linked by common intermediates.
Now you might be asking: if ATP is so unstable, how does it get formed in the first place and how can it be found at such high concentrations? The short answer involves two ideas that we have encountered before: first, while ATP is unstable (like wood in the presence of O2), its hydrolysis does involve overcoming an activation energy and so under physiological conditions, an enzyme that can catalyze and coupled the hydrolysis of ATP to other reactions (an ATPase) is needed; second, ATP is formed through coupled reactions that link the oxidation of molecules such as glucose or through the direct absorption of energy in the form of light (photosynthesis). When glucose reacts with oxygen it forms carbon dioxide and water:
C6H12O6 + 6O2 ⇄ 6CO2 + 6H2O
with an overall standard free energy change ΔGº = – 2870 kJ/mol. The reasons for this high negative free energy change are that ΔSº is positive (why do you think this is?), and there is a large negative ΔHº change. Remember that ΔHº can be approximated by looking at the changes in bond energy from reactants to products. A major reason for this high enthalpy change is that the bond energies in carbon dioxide and water are very high (a C=O bond takes 805 kJ/mol to break, and an O-H bond 463 kJ/mol), and therefore when C=O and O-H bonds are formed a large amount of energy is released. When one mole of glucose is completely oxidized to CO2 and H2O, the energy produced is harnessed to ultimately produce ~36 moles of ATP (from ADP and Pi).
The mechanism(s) involved in this process are complex (involving intervening ion gradients and rotating enzymes), but the basic principle remains: the reactions are coupled by common and often complex intermediate processes. This reaction coupling leads to networks of reactions. The synthesis and reaction of ATP (and ADP) is governed by the same principles that govern much simpler reactions. Whether or not ATP or ADP is the dominant species in any cellular compartment depends upon the conditions and what substrates are present to form a reaction.
Questions
Questions to Answer
- Can you draw the protonated form of ATP?
- Can you draw the unprotonated form of ATP, showing how the negative charge is stabilized by the surrounding cellular fluids? (Hint: the fluid is mainly water.)
- The pKas of phosphoric acid (H3PO4) are 2.15, 7.2 and 12.35. Is the ATP protonated or deprotonated in the cellular environment?
- Write out a hypothetical sequence of two reactions that result in the production of a thermodynamically unfavorable product.
- How can you tell whether two reactions are coupled?
- Why do biological systems rely on coupled reactions?
- If ATP is unstable, how is it possible that ATP can exist at high concentrations within the cell?
Questions to Ponder
- If you are trying to determine if two reactions are coupled, what do you look for?
- Coupling allows unfavorable reactions to occur. Why doesn’t this violate the laws of thermodynamics?Assume that you have a set of five coupled reactions. What factors could complicate the behavior of the system?
- How could you insure that an unfavorable reaction continued to occur at a significant (useful)
rate?
- Of course this designation is entirely arbitrary, as backward and forward depend on how the initial reaction is written. ↵
- We recognize such evolutionarily conserved processes because they used essentially (but not quite) the same reaction components and strategies. For example, aerobic respiration (whether in bacteria, potatoes, or humans) uses a structurally similar membrane system to transfer electrons from molecule to molecule (redox reaction). This generates an H+ gradient then used by a rotatory protein “generator” to synthesize ATP. ↵
- Amino acid chains are referred to as polypeptides; a protein is a functional unit, which can be composed of multiple polypeptides and non-polypeptide components such as heme groups. ↵
- http://benbleasdaleblogs.wordpress.com/2013/10/23/want-to-see-an-enzyme-check-inside-your-nose/ ↵
- This binding site can also be occupied by other types of molecules, in particular carbon monoxide (CO). Because the binding of O2 to hemoglobin is much weaker and less stable than the CO– hemoglobin interaction, exposure to CO blocks O2 transport through the body, leading to suffocation. ↵
- An explanation of how to do this is provided in the supplementary materials. ↵
- It is always important to keep in mind that even though we write reaction equations with “sides” – product and reactant – in fact all these species are present in the same reaction vessel. ↵
- By adding a small amount of solute (rather than a volume of solution) we will not significantly affect the volume of the solution - which will make determining the concentration easier. ↵
- You might wonder why the amide nitrogen is not basic - even though it appears to have a lone pair of electrons. However these electrons are not available for donation because they are conjugated (interacting) with the C=O group. You will have to wait until organic chemistry to hear more on this fascinating topic ↵
- calculated from ΔGº = –RTlnK at physiologycal temperature 37 ℃ ↵
- This occurs primarily because O2 is in short supply and the aerobic respiration reaction cannot proceed to completion. ↵
- Guyenet et al, 2010. Central CO2 chemoreception and the integrated neural mechanisms of cardiovascular and respiratory control. J. Appl. Physiol. [online] 2010. 108, 995. http://www.ncbi.nlm.nih.gov/pubmed/20075262. ↵
- Although it does not explain why we would want to exercise in the first place. ↵
- Adapted from Physical Chemistry for the Chemical and Biological Sciences by Raymond Chang [complete citation] ↵

