8 How Far? How Fast?
Melanie M. Cooper and Michael W. Klymkowsky

After our overview of common chemical reactions in Chapter 7, the next questions on your mind may well be what determines whether or not a reaction will happen, how fast it will go, how far it will go, or whether it will go in the forward or reverse direction? What causes gasoline to suddenly combust in a violent explosion whereas an iron nail slowly rusts over many years? Are these mysteries of the universe, or can we untangle them in some coherent way?
Once again, it turns out that the universe behaves in an orderly way, and by paying attention to various experimental observations, chemists over the last few centuries have come to understand the factors that control the rate, extent, and direction of reactions. The subject of rate and extent will lead us back to thermodynamics and Gibbs free energy, as we work out the molecular reorganizations that occur during the forward and reverse reactions. In this chapter, we introduce concepts that will allow us to consider how fast a reaction occurs and predict how far it will go.
8.1 What Factors Control Reactions?
The key to understanding the behavior of chemical reactions is to remember that: (a) chemical reactions are systems in which reactants and products interact with their environment and (b) at the molecular level, all reactions are reversible, even though some reactions may seem irreversible. For example, once a log starts burning, we cannot easily reassemble it from carbon dioxide (CO2), water (H2O), and energy. But in fact, we can reassemble the log in a fashion by allowing a tree to grow, and by using CO2 from the air, H2O from the ground, and energy from the sun (photosynthesis). However, this type of reverse (or backward) reaction is far more complex and involved than the simple forward reaction of burning.
There are, however, a number of factors that we can use to predict how fast and how far a particular reaction will go, including the concentration of the reactants, the temperature, the type of reaction, and the presence of a catalyst. The concentrations of molecules and the temperature of the system are important because all reactions involve collisions between molecules (except for reactions driven by the absorption of light—and you could view those as collisions of a sort). The concentration of reactants determines how often various types of collisions take place (i.e., the more molecules per unit volume, the more frequently collisions occur), whereas the temperature determines the energetics of the collisions: recall that there is a distribution of kinetic energies of molecules at a particular temperature, so not all collisions will lead to a reaction. Molecular structure also matters because it determines whether or not collisions are productive. The only collisions that work are those in which molecules hit each other in particular orientations and with particular energies.
As a reaction proceeds, and reactants are converted into products, the probability of reactant molecules colliding decreases (since there are fewer of them) while the probability of product molecules colliding increases. That is the rate of the forward reaction slows down and the rate of the reverse reaction speeds up This will continue until the rates of the forward reaction and the backward reaction are equal, and the system reaches equilibrium: the point at which no more macroscopic changes occur and the concentrations of reactants and products remain constant at the macroscopic scale.[1] However, as we will discuss further, the forward and back reactions have not stopped, and if we could see the molecules we would see both forward and back reactions still occurring, although there is no overall change in concentration.
As an example, Brønsted–Lowry acid–base reactions are very fast because the probability that the reaction occurs per unit of time is high. When an acid and a base are mixed together, they react immediately with no waiting and without the addition of heat. For example, if we dissolve enough hydrogen chloride gas (HCl) in water to make a 0.1 M solution of hydrochloric acid, the pH immediately drops from 7 (the pH of water) to 1.[2] This measurement tells us that all the HCl has ionized, to give: [H+] = 0.1 and [Cl–] = 0.1.
Now let us take the case of acetic acid (CH3COOH). If we dissolve enough acetic acid in water to make a 0.1-M solution, the pH of the solution immediately changes from pH 7 (pure water) to 2.9 (not 1). Even if you wait (as long as you want) the pH stays constant, around 3. You might well ask, “What is going on here?” The acid–base reaction of acetic acid and water is fast, but the pH is not as low as you might have predicted. We can calculate the [H+] from the pH, again using the relationship pH = – log [H+] and [H+] = 10-pH, giving us a value of [H+] = 1.3 x 10–3 M. Thus, the concentration of H+ is more than two orders of magnitude less than you might have expected! If you think about this, you will probably conclude that the amount of acetic acid (AcOH)[3] that actually reacted with the water must have been very small indeed. In fact we can calculate how much acetic acid reacted using the relationships from the equation:
AcOH + H2O ⇄ H3O+ + AcO–
If the concentration of acetic acid started at 0.10 M, and after the ionization reaction 1.3 x 10–3 M of H+ are present, then the final concentration of acetic acid must be (0.10 minus 1.3 x 10–3) M. If we use the appropriate number of significant figures, this means that the concentration of acetic acid is still 0.10 M (actually 0.0986 M).
There are two important conclusions here: first, the reaction of acetic acid is fast, and second, most of the acetic acid has not, in fact, reacted with the water. But wait—there is more! Even if the reaction appears to have stopped because the pH is not changing any further, at the molecular level things are still happening. That is, the reaction of acetic acid with water continues on, but the reverse reaction occurs at the same rate. So the bulk concentrations of all the species remain constant, even though individual molecules present in each population are constantly changing.[4] The questions of how far a reaction proceeds (towards products) and how fast it gets there are intertwined. We will demonstrate the many factors that affect these two reaction properties.
Questions
Questions to Answer
- Draw out a general Brønsted–Lowry acid–base reaction that might occur in water.
- Why do you think the reaction occurs so fast (as soon as the molecules bump into each other)?
- Do you think the water plays a role in the reaction? Draw out a molecular-level picture of your acid–base reaction, showing the solvent interactions.
Question to Ponder
- How do you think the reaction would be affected if it took place in the gas phase instead of an aqueous solution?
8.2 Reaction Rates
In science, when we talk about a rate we mean the change in a quantity over time. A few non-chemical examples include: certain investments with an interest rate, which is the increase in the principle over time (if the rate is negative, then it means that the amount of principle is decreasing over time—not a good investment!); your speed, which is the rate at which you travel down the road, given in miles per hour (or kilometers per hour); a child’s growth rate, which might be an inch or two per year (while the elderly might shrink at a different rate); and the growth rate of some plants, like kudzu, which can grow at a rate of 12 inches per day. The units of rate are an amount divided by a period of time. This might seem too obvious to dwell on, but it is worth noting that most real processes do not have a constant rate of change; rates themselves can and do change. This is one reason why calculus is useful in chemistry: it provides the mathematical tools needed to deal with changing rates, like those associated with planetary motions, falling bodies, and (it turns out) chemical reactions.
If we apply the idea of an amount divided by a period of time to the speed of a chemical reaction, what can we measure to determine a reaction’s rate? What units tell us the amount present, in the same way that miles and meters measure distance? We can’t use mass, because reactions occur between particles (atoms, molecules, ions), which have different masses. We must use the unit that tells us how many particles of a particular type there are—moles. Furthermore, because most reactions (particularly the ones involved in biological and environmental systems) occur in aqueous solutions or in the atmosphere, we usually use units of concentration—molarity (M, mol/L)—to describe the amount of a substance taking part in or produced by a reaction. Typically, the concentration of substance A2 is written [A2], and the rate of a reaction can be described as the change in concentration of a reactant or product over a unit of time. So, Δ[A2]/Δt or [A2]2 –[A22]1 / t2 –t1, where [A2]2 is the concentration at time t2, and [A2]1 is the concentration at time t2(assuming that t2 occurs later in time than t1).
Reaction Rates and Probabilities
Let us now step back and think about what must happen in order for a reaction to occur. First, the reactants must be mixed together. The best way to make a homogeneous mixture is to form solutions, and it is true that many reactions take place in solution. When reactions do involve a solid, like the rusting of iron, the reactants interact with one another at a surface. To increase the probability of such a reaction, it is common to use a solid that is very finely divided, so that it has a large surface area and thus more places for the reactants to collide.[5]
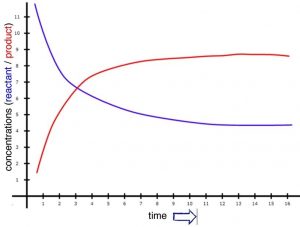
We will begin with a more in-depth look at reaction rates with a simple hypothetical reaction that occurs slowly, but with a reasonable rate in solution. Our hypothetical reaction will be A2 + B2 ⇄ 2AB. Because the reaction is slow, the loss of reactants (A2 + B2) and the production of product (AB) will also be slow, but measurable. Over a reasonable period of time, the concentrations of A2, B2, and AB change significantly. If we were to watch the rate of the forward reaction (A2 + B2 ⇄ 2AB), we would find that it begins to slow down. One way to visualize this is to plot the concentration of a reactant versus time (as shown in the graph). We can see that the relationship between them is not linear, but falls off gradually as time increases. We can measure rates at any given time by taking the slope of the tangent to the line at that instant.[6] As you can see from the figure, these slopes decrease as time goes by; the tangent at time = 0 is much steeper than the tangent at a later time. On the other hand, immediately after mixing A2 + B2, we find that the rate of the backward reaction (that is: 2AB ⇄ A2 + B2) is zero, because there is no AB around to react, at least initially. As the forward reaction proceeds, however, the concentration of AB increases, and the backward reaction rate increases. As you can see from the figure, as the reaction proceeds, the concentrations of both the reactants and products reach a point where they do not change any further, and the slope of each concentration time curve is now 0 (it does not change and is “flat”).
Let us now consider what is going on in molecular terms. For a reaction to occur, some of the bonds holding the reactant molecules together must break, and new bonds must form to create the products. We can also think of forward and backward reactions in terms of probabilities. The forward reaction rate is determined by the probability that a collision between an A2 and a B2 molecule will provide enough energy to break the A—A and B—B bonds, together with the probability of an AB molecule forming. The backward reaction rate is determined by the probability that collisions (with surrounding molecules) will provide sufficient energy to break the A—B bond, together with the probability that A–A and B–B bonds form. Remember, collisions are critical; there are no reactions at a distance. The exact steps in the forward and backward reactions are not specified, but we can make a prediction: if these steps are unlikely to occur (low probability), the reactions will be slow.
As the reaction proceeds, the forward reaction rate decreases because the concentrations of A2 and B2 decrease, while the backward reaction rate increases as the concentration of AB increases. At some point, the two reaction rates will be equal and opposite. This is the point of equilibrium. This point could occur at a high concentration of AB or a low one, depending upon the reaction. At the macroscopic level, we recognize the equilibrium state by the fact that there are no further changes in the concentrations of reactants and products. It is important to understand that at the molecular level, the reactions have not stopped. For this reason, we call the chemical equilibrium state a dynamic equilibrium. We should also point out that the word equilibrium is misleading because in common usage it often refers to a state of rest. In chemical systems, nothing could be further from the truth. Even though there are no macroscopic changes observable, molecules are still reacting.[7]
Questions
Questions to Answer
- What does linear mean (exactly) when referring to a graph?
- Imagine you are driving at a constant speed of 60 miles per hour. Draw a graph of distance versus time, over a time period of four hours.
- How would you determine your speed from the graph (assuming you did not already know the answer)?
- Now imagine you take your foot off the accelerator and the car coasts to a stop over the course of one hour. What is the average speed over the last hour? How would you figure that out?
- What is the speed exactly 30 minutes after you take your foot off the brake? How would you figure that out?
- Consider the reaction A2 + B2 ⇄ 2AB. If the rate of the forward reaction = – Δ[A2]/Δt (at a given time). How would you write the rate in terms of [B2] or in terms of [AB]?
- How does the rate of the forward reaction change over time? Does it increase, decrease or stay the same? Why?
- What does a probability of “0” mean?
- How do we know that, at equilibrium, the forward and reverse reactions are still occurring.
- Design an experiment that would allow you to investigate whether a reaction had stopped:at the macroscopic level and at the molecular level
Questions to Ponder
- Why can a macroscopic reaction be irreversible, even though at the molecular level reaction is reversible?
- Under what conditions (if any) would a reaction stop completely?
- Why are molecular level and macroscopic behaviors different?
Questions for Later
- Why do you think the amounts of products and reactants do not change after a certain time?
- What is the observable rate of reaction after the time when the concentrations of products and reactants change?
8.3 Kinetics and the Mechanisms of Reactions
The study of reaction rates, called chemical kinetics, encompasses a wide range of activities, measurements, and calculations. You might wonder why anyone would bother with this, but it turns out that we can use kinetic data to get more information about a reaction than just how fast it goes; we can find out about the pathway that the reaction takes from reactants to products, known as the mechanism of the reaction. If you think about a reaction in molecular terms, it seems clear that there must be a continuous pathway between reactants and products. The reactants do not suddenly disappear and then reappear as products, and in most reactions only one or two bonds are broken and formed as the reaction proceeds. This pathway, or mechanism, denotes the order in which bonds are broken and formed, and the intermediate species involved. However, because we cannot see directly what happens at the molecular level during a reaction, we have to rely on indirect methods to determine what is going on. Even using modern spectroscopic techniques, discussed in more detail in the spectroscopy section, some species in reaction pathways may only be present for femto (10–15) or atto (10–18) seconds. Events on these time scales are difficult to study, and in fact much of the current cutting edge research in chemistry and physics is directed at detecting and characterizing such ephemeral molecular-level events. As we will see, information about how the reaction rate varies with concentration and temperature can give us fascinating chemical insights into reaction pathways.
Concentrations and Reaction Rates
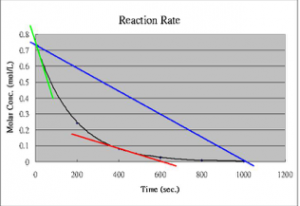
As we have seen as the probability of collisions between reactant molecules increases, the rate of reaction increases. In order to get information about the reaction mechanism we need to know the exact relationship between concentrations and rates. This can be done using a number of different techniques and experimental set-ups. But before we do that, we need to go over a few more terms. Recall that the rate of the reaction is the change in concentration of reactant per unit time. If the time interval is measurable and real, the rate we get is called the average rate (over that time interval), as shown in the earlier graph. If we imagine that the time interval drops to 0, we get the instantaneous rate, which is the slope of the tangent to the concentration versus time curve at a given time (more calculus). The rate at the beginning of the reaction can be obtained by taking the tangent at the start of the reaction (t = 0). This initial rate is useful in many situations because as the reactants form products, these products can interfere with or inhibit the forward reaction. This is particularly true in biological systems, where a product may influence its own formation. For example, it can bind to a site on the enzyme that catalyzes the reaction. This type of interaction is common, and often inhibits the enzyme’s activity (a form of feedback regulation).
We can measure the initial rate for a reaction using different initial concentrations of reactants. Using an appropriate experimental design, we can figure out how the rate of the reaction varies with each reactant. For many common reactions, the relationship between the rate and the concentration is fairly straightforward. For example, in the reaction:
(CH3)3CBr + –OH + Na+ ⇄ (CH3)3COH + Br– + Na+,
the rate is dependent only on the concentration of t-butyl bromide [(CH3)3CBr], not on the concentration of the sodium ion [Na+] or the hydroxide ion [–OH]. “But why only the t-butyl bromide?” you might well ask. We will get to that point shortly, because it gives us some very interesting and important insights into the reaction mechanism. First, let us delve into a bit more background.
Because the rate is directly proportional to the [(CH3)3CBr], we can write the relationship between rate and concentration as: rate ∝ [(CH3)3CBr], or we can put in a constant (k) to make the equation:
rate = k[(CH3)3CBr]
We could also write
–Δ[(CH3)3CBr] /Δt = k[(CH3)3CBr],
or if we let the time interval drop to zero,
–d[(CH3)3CBr] /dt = k[(CH3)3CBr].
In all these forms, the equation is known as the rate equation for the reaction. The rate equation must be experimentally determined. It is worth noting that you cannot write down the rate equation just by considering the reaction equation. (Obviously, in this case, –OH or Na+ do not appear in the rate equation.) The constant (k) is known as the rate constant and is completely different from the equilibrium constant (Keq). The fact that they are both designated by k (one lower case and one upper case) is just one of those things we have to note and make sure not to confuse. A rate equation that only contains one concentration is called a first-order rate equation, and the units of the rate constant are 1/time.
Now, in contrast to the first-order reaction of methyl bromide and hydroxide, let us compare the reaction of methyl bromide with hydroxide:[8]
CH3Br + –OH + Na+ ⇄ CH3OH + Br– + Na+,
For all intents and purposes, this reaction appears to be exactly the same as the one discussed on the previous page. That is, the bromine that was bonded to a carbon has been replaced by the oxygen of hydroxide.[9] However, if we run the experiments, we find that the reaction rate depends on both the methyl bromide concentration [CH3Br] and on the hydroxide concentration [–OH]. The rate equation is equal to k [CH3Br] [–OH]. How can this be? Why the difference? Well, the first thing it tells us is that something different is going on at the molecular level; the mechanisms of these reactions are different.
Reactions that depend on the concentrations of two different reactants are called second-order reactions, and the units of k are different (you can figure out what they are by dimensional analysis). In general:
rate = k [A] first order
rate = k [A][B] second order (first order in A and first order in B)
rate = k [A]2 second order (in A)
rate = k [A]2[B] third order (second order in A and first order in B).
There are a number of methods for determining the rate equation for a reaction. Here we will consider just two. One method is known as the method of initial rates. The initial rate of the reaction is determined for various different starting concentrations of reactants. Clearly, the experimental design is of paramount importance here. Let us say you are investigating our reaction A + B ⇄ 2AB. The rate may depend on [A] and/or [B]. Therefore, the initial concentrations of [A] and [B] must be carefully controlled. If [A] is changed in a reaction trial, then [B] must be held constant, and vice versa (you cannot change both concentrations at the same time because you would not know how each one affects the rate).
The method of initial rates requires running the experiment multiple times using different starting concentrations. By contrast, the graphical method involves determining the rate equation from only one run of the reaction. This method requires the collection of a set of concentration versus time data (the same data that you would collect to determine the rates). Ideally we would like to manipulate the data so that we can obtain a linear equation (y = mx + b). For example, if we have a set of [A] versus time data for a reaction, and we assume the reaction is first order in A, then we can write the rate equation as: -d[A]/dt =k[A].
Now, if we separate the variables [A] and t to get: -d[A]/[A] =kt. We can then integrate the equation over the time period t = 0 to t = t to arrive at:
ln [A]t = –kt + [A]0.[10]
You will notice that this equation has the form of a straight line; if we plot our data (ln [A] versus t) and if the reaction is first order in [A], then we should get a straight line, where the slope of the line is –k. We can do a similar analysis for a reaction that might be second order in [A]:
rate = k[A]2.
In this case, we can manipulate the rate equation and integrate to give the equation:
1/[A]t = kt + 1/[A]0.
Therefore, plotting 1/[A] versus t would give a straight line, with a slope of k, the rate constant. This method of analysis quickly becomes too complex for reactions with more than one reactant (in other words, reactions with rates that depend on both [A] and [B]), but you can look forward to that in your later studies!
| Order | Rate Law | Integrated Rate Law | Graph for Straight Line | Slope of Line |
| 0 | Rate = k | [A]t =-kt + [A]0 | [A] vs. t | –k |
| 1 | Rate = k[A] | ln[A]t =-kt + ln[A]0 | ln [A] vs. t | –k |
| 2 | Rate = k[A]2 | 1/[A]t = kt + 1/[A]0 | 1/[A] vs. t | k |
The two approaches (multiple runs with different initial conditions and the graphical method finding the best line to fit the data) provide us with the rate law. The question is, what does the rate law tell us about the mechanism? We will return to this question at the end of this chapter.
Questions
Questions to Answer
- It turns out that most simple reactions are first or second order. Can you think why?
- Design an experiment to determine the rate equation for a reaction 2A + B ⇄ C. Using the method of initial rates and a first experimental run using 0.1-M concentrations of all the reactants, outline the other sets of conditions you would use to figure out what that rate equation is.
- What is the minimum number of runs of the reaction that you would have to do?
- How would you determine the rate for each of your sets of conditions?
- Now imagine you have determined that this reaction 2A + B ⇄ C does not depend on [B]. Outline a graphical method you could use to determine the rate equation. What data would you have to collect? What would you do with it?
Questions for Later
- Why do you think it is that we cannot just write the rate equation from the reaction equation?
- Why do you think that the most common rate equations are second order?
Temperature and Reaction Rates
Temperature is another important factor when we consider reaction rates. This makes sense if you remember that the vast majority of reactions involve collisions and that the effects of collisions are influenced by how fast the colliding objects are moving. We know intuitively that heating things up tends to make things happen faster. For example, if you want something to cook faster you heat it to a higher temperature (and cooking, as we know, is just a series of chemical reactions). Why is this so? If we consider the reaction of hydrogen and oxygen, discussed in Chapter 7, which is a highly exothermic reaction—explosive, in fact. Yet a mixture of hydrogen and oxygen is quite stable unless energy is supplied, either by heating or a spark of electricity. The same is true of wood and molecular oxygen. The question is: What is the initial spark of energy being used for?
The answer lies within one of the principles that we have returned to over and over again: When atoms form bonds, the result is a more stable system, compared to the energy of non-bonded atoms. But not all bonds are equally stable; some are more stable than others. Nevertheless, energy is always required to disrupt a bond—any bond. If a reaction is to take place, then at least one of the bonds present in the reactants must be broken, and this requires energy.
Imagine two reactants approaching each other. As the reaction starts to occur, the first thing that happens is that at least one bond in a reactant molecule must start to break. It is the initial, partial-bond-breaking step that requires an input of energy from the molecule’s surroundings, and the amount of energy required and available will determine if the reaction occurs. If the amount of energy in the environment is not enough to begin the breaking of bonds in the reactants (for example, in the burning of wood, large amounts of energy are required for the initial bond breaking), then the reaction will not occur without an energy “push”. Wood does not just burst into flames (at least at standard temperatures)—and neither do humans.[11] The burning wood reaction, wood + O2 ⇄ H2O + CO2, does not occur under normal conditions, but if the temperature increases enough, the reaction starts. Once the reaction starts, however, the energy released from the formation of new bonds is sufficient to raise the local temperature and lead to the breaking of more bonds, the formation of new ones, and the release of more energy. As long as there is wood and oxygen available, the system behaves as a positive and self-sustaining feedback loop. The reaction will stop if one of the reactants becomes used up or the temperature is lowered.
It is the activation energy associated with reactions that is responsible for the stability of our world. For example, we live in an atmosphere of ~20% oxygen (O2). There are many molecules in our bodies and in our environment that can react with O2. If there were no energy barriers to combustion (i.e., reaction with O2), we would burst into flames. Sadly, as Salem witches and others would have attested (if they could have), raise the temperature and we do burn. And once we start burning, it is hard to stop the reaction. As we have said before, combustion reactions are exothermic. Once they have produced enough thermal energy, the reaction doesn’t need that spark any more. But that initial spark needs the addition of energy (such as the kind provided by a detonator) for explosions to occur.
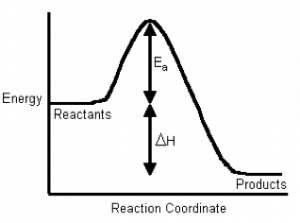
If we plot energy versus the progress of the reaction, we can get a picture of the energy changes that go on during the reaction. Remember that the reaction coordinate on the x-axis is not time; we have seen that reactions go backwards and forwards all the time. For a simple one-step reaction as shown in the figure, the highest point on the energy profile is called the transition state. It is not a stable entity and only exists on the timescale of molecular vibrations (femtoseconds). The energy change between the reactants and the transition state is called the activation energy. This is the energy that must be supplied to the reactants before the reaction can occur. This activation energy barrier is why, for example, we can mix hydrogen and oxygen and they will not explode until we supply a spark, and why we can pump gasoline in an atmosphere that contains oxygen, even though we know that gasoline and oxygen can also explode. The amount of energy that must be supplied to bring about a reaction is a function of the type of reaction, some reactions (acid base) have low activation energies and correspondingly high rates, and some (rusting) have high activation energies and low rates.
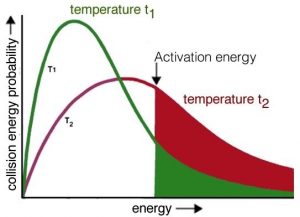
Now it should be easier to understand how increasing temperature increases the reaction rate—by increasing the average kinetic energy of the molecules in the environment. Recall that even though individual molecules have different kinetic energies, all of the different populations of molecules in a system have the same average kinetic energy. If we consider the effect of temperature on the Maxwell–Boltzmann distribution of kinetic energies, we see right away that at higher temperatures there are relatively more molecules with higher kinetic energy. Collisions between these high-energy molecules provide the energy needed to overcome the activation energy barrier, that is, the minimum energy required to start a chemical reaction. As the temperature rises, the probability of productive collisions between particles per unit time increases, thus increasing the reaction rate. At the same time, it is possible that raising the temperature will allow other reactions to occur (perhaps reactions we have not been considering). This is particularly likely if we are dealing with complex mixtures of different types of molecules.
The rate equation does not appear to contain a term for temperature, and typically we have to specify the temperature at which the rate is measured. However, because the rate changes with temperature, it must be the rate constant that changes. Sure enough, it has been determined experimentally that the rate constant is k can be described by the equation
k= Ae–Ea/RT,
where k is the rate constant, Ea is the activation energy, T is the temperature, and R and A are constants.[12] This is known as the Arrhenius equation. As you can see, k is directly proportional to the temperature, and indirectly proportional to the activation energy Ea. The constant A is sometimes called the frequency factor and has to do with the collision rate. A changes depending on the specific type of reaction (unlike R, the gas constant, which does not change from reaction to reaction). One way of thinking about the rate constant is to consider it as a representation of the probability that a collision will lead to products: the larger the rate constant, the more frequently productive collisions occur and the faster the reaction.
The activation energy for a reaction also depends upon the type of reaction that is occurring. For example, a Brønsted–Lowry acid–base reaction has a very low activation energy barrier. In these reactions the only thing that is happening is that a proton is being transferred from one electronegative element to another:
H—Cl + H—O—H ⇄ Cl– + H3O+
(draw this out to better see what is happening).
The reaction is rapid because the Cl—H bond is highly polarized and weak. In a sense, it is already partially broken. Also, these reactions usually take place in water, which interacts with and stabilizes the growing charges. Low-energy collisions with water molecules are sufficient to finish breaking the Cl—H bond. We say that acid–base reactions like this are kinetically controlled because they occur upon mixing and do not require heating up or extra energy to proceed. Essentially all collisions involving the HCl molecule provide sufficient energy to break the H—Cl bond. This is also true for almost all proton-transfer reactions. However, for most other types of reactions, simply mixing the reactants is not enough. Energy must be supplied to the system to overcome this energy barrier, or we have to wait a long time for the reaction to occur. In fact, most organic reactions (those in which carbon is involved) are quite slow. Why the difference? The answer should be reasonably obvious. There is simply not enough energy in the vast majority of the collisions between molecules to break a C—H, C—C, C—N, or C—O bond. If you take organic chemistry lab, you will discover that large portions of time are spent waiting as solutions are heated to make reactions happen faster. As we mentioned before, this is quite fortunate. As we mentioned before, this is quite fortunate, since we are (basically) organized by chance and natural selection, from collections of organic reactions. If these reactions occurred spontaneously and rapidly, we would fall apart and approach equilibrium (and equilibrium for living things means death!). You may already see the potential problem in all of this: it is generally not advisable to heat up a biological system, but we certainly need biological systems to undergo reactions. Biological systems need different reactions to proceed in different places and at different rates, without being heated up. For this, biological systems (and many other types of systems) use a wide range of catalysts, the topic of our next section.
Questions
Questions to Answer:
- When a reaction releases energy, where does the energy come from?
- There is a rule of thumb that increasing the temperature by 10°C will double the rate for many reactions.
- What factor in the Arrhenius equation is always changing?
- Explain why the reaction rate increases when the temperature increases.
8.4 Catalysis
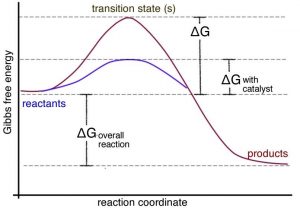
A catalyst provides an alternate pathway for a reaction to occur. More importantly, this pathway usually involves a lower activation energy than the uncatalyzed pathway, as shown in the graph. This means that the rate of the reaction can increase. It can do so because at a given temperature, collisions with enough energy to overcome the new lower activation energy barrier occur more frequently. But because the catalyst is neither a reactant nor a product of the reaction, it does not influence the reaction’s overall energy change. In biological systems, there are protein and RNA-based catalysts (enzymes and ribozymes); in non-living systems, minerals and metals often act as catalysts. Even simple species such as protons can be considered catalysts. Anything that is unchanged at the start and at the end of the reaction can be considered a catalyst. There are many different mechanisms through which catalysts can act. Biological catalysts are generally very selective in terms of the reactions they catalyze and very effective in speeding reactions up. It is not uncommon for the rate of a catalyzed reaction to be millions of times faster than the uncatalyzed reaction. In a complex reaction system, speeding up one reaction at the expense of others can have profound effects. However, there are also many examples where enzymes catalyze “off-target” reactions of the same or different types (although these reactions are generally accelerated to a much lesser extent). This ability to catalyze a range of reactions occurs because the surfaces of enzyme molecules are complex and often accommodate and bind a range of molecules. In other words, they are promiscuous.[13] The common analogy of an enzyme as a lock and the reactant molecules are viewed as the unique key, but this is far too simplistic. In reality, there are many molecules that can bind to a specific active site in an enzyme with greatly varying affinities. Although the mode of action of enzymes varies, in many cases the active site holds the two reactive molecules in close juxtaposition, which can speed their reaction. Can you imagine why?[14]
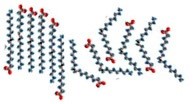
An organic chemical reaction that requires a catalyst is the addition of hydrogens across a C=C bond. Without the catalyst, this reaction would not occur on a human timescale. It is an important reaction in many pharmaceutical syntheses and in the production of fat (solid) from oil (liquids). For example, margarine is produced by adding hydrogen to the C=C bonds of oils extracted from plants, as shown in the figure. The removal of the C=C bond makes the molecules pack better together. This is because London dispersion forces can now act upon the whole length of the molecule, increasing the strength of the van der Waals interactions between the molecules. Thus, the hydrogenated oil is a solid at room temperature. The catalyst is usually a transition metal, palladium (Pd) or platinum (Pt), finely divided and adsorbed onto the surface of an inert substance like charcoal (carbon), as shown in the figure. The transition metal has empty d orbitals that interact with the C=C bond’s pi orbital, destabilizing the pi bond and making it more susceptible to reaction. H2 molecules also adsorb onto (interact with) the surface of the transition metal and insert themselves between the C and the catalyst, forming a fully-hydrogenated fat. Unfortunately, in many cases the hydrogen does not add across the double bond. Instead, the bond isomerizes from cis to trans, forming the unnatural trans isomer which has been implicated in the development of heart disease.[15]
Questions
Questions to Answer
- Draw a representation of an enzyme active site. What kinds of interactions do you think hold the substrate molecule in the active site?
- Why do you think binding two reactants in close proximity will increase the reaction rate?
8.5 Equilibrium
Now that we have a good idea about the factors that affect how fast a reaction goes, let us return to a discussion of what factors affect how far a reaction goes. As previously discussed, a reaction reaches equilibrium when the rate of the forward reaction equals the rate of the reverse reaction, so the concentrations of reactants and products do not change over time. The equilibrium state of a particular reaction is characterized by what is known as the equilibrium constant, Keq.
We can generalize this relationship for a general reaction:
nA + mB ⇄ oC + pD.
![An image of an equation. Starting of with the Keq equals. The numerator has "[C]^0[D]^0" and is labeled as products. And the denominator is "[A]^n[B]^m" and is labeled as reactants.](https://openbooks.lib.msu.edu/app/uploads/sites/12/2019/11/ch08-08_Keq.jpg) Note that each concentration is raised to the power of its coefficient in the balanced reaction. By convention, the constant is always written with the products on the numerator, and the reactants in the denominator. So large values of Keq indicate that, at equilibrium, the reaction mixture has more products than reactants. Conversely, a small value of Keq (typically <1, depending on the form of Keq) indicates that there are fewer products than reactants in the mixture at equilibrium. The expression for Keq depends on how you write the direction of the reaction. You can work out for yourself that Keq(forward) = 1/Keq(reverse). One other thing to note is that if a pure liquid or solid participates in the reaction, it is omitted from the equilibrium expression for Keq. This makes sense because the concentration of a pure solid or liquid is constant (at constant temperature). The equilibrium constant for any reaction at a particular temperature is a constant. This means that you can add reactants or products and the constant does not change.[16] You cannot , however, change the temperature, because that will change the equilibrium constant as we will see shortly. The implications of this are quite profound. For example, if you add or take away products or reactants from a reaction, the amounts of reactants or products will change so that the reaction reaches equilibrium again—with the same value of Keq. And because we know (or can look up and calculate) what the equilibrium constant is, we are able to figure out exactly what the system will do to reassert the equilibrium condition.
Note that each concentration is raised to the power of its coefficient in the balanced reaction. By convention, the constant is always written with the products on the numerator, and the reactants in the denominator. So large values of Keq indicate that, at equilibrium, the reaction mixture has more products than reactants. Conversely, a small value of Keq (typically <1, depending on the form of Keq) indicates that there are fewer products than reactants in the mixture at equilibrium. The expression for Keq depends on how you write the direction of the reaction. You can work out for yourself that Keq(forward) = 1/Keq(reverse). One other thing to note is that if a pure liquid or solid participates in the reaction, it is omitted from the equilibrium expression for Keq. This makes sense because the concentration of a pure solid or liquid is constant (at constant temperature). The equilibrium constant for any reaction at a particular temperature is a constant. This means that you can add reactants or products and the constant does not change.[16] You cannot , however, change the temperature, because that will change the equilibrium constant as we will see shortly. The implications of this are quite profound. For example, if you add or take away products or reactants from a reaction, the amounts of reactants or products will change so that the reaction reaches equilibrium again—with the same value of Keq. And because we know (or can look up and calculate) what the equilibrium constant is, we are able to figure out exactly what the system will do to reassert the equilibrium condition.
Let us return to the reaction of acetic acid and water:
AcOH + H2O ⇄ H3O+ + AcO–,
we can figure out that the equilibrium constant would be written as:
Keq = [H3O+][AcO–]/[AcOH].
The H2O term in the reactants can be omitted even though it participates in the reaction, because it is a pure liquid and its concentration does not change appreciably during the reaction. (Can you calculate the concentration of pure water?) We already know that a 0.10-M solution of AcOH has a pH of 2.9, so we can use this experimentally-determined data to calculate the equilibrium constant for a solution of acetic acid. A helpful way to think about this is to set up a table in which you note the concentrations of all species before and after equilibrium.
| [AcOH] M | [H3O+] | [AcO–] M | |
| Initial Concentration | 0.10 | 1 x 10–7 (from water) | 0 |
| Change in Concentration (this is equal to the amount of AcOH that ionized – and can be calculated from the pH) | – 1.3 x 10–3 M
(because the AcOH must reduce by the same amount that the H+ increases) |
10–pH
= 1.3 x 10–3 M |
1.3 x 10–3 M (because the same amount of acetate must be produced as H+) |
| Final
(equilibrium concentration) |
0.10 – 1.3 x 10–3
~ 0.10 |
(1.3 x 10–3)
+ (1 x 10–7) ~ 1.3 x 10–3 |
1.3 x 10–3 |
You can also include the change in concentration as the system moves to the equilibrium state: AcOH + H2O ⇄ H3O+ + AcO–. Using the data from this type of analysis, we can calculate the equilibrium constant: Keq = (1.3 x 10–3)2/0.1, which indicates that Keq for this reactions equals 1.8 x 10–5. Note that we do not use a large number of significant figures to calculate Keq because they are not particularly useful, since we are making approximations that make a more accurate calculation not justifiable. In addition, note that Keq itself does not have units associated with it.
Free Energies and Equilibrium Constants
Now we can calculate the equilibrium constant Keq, assuming that we can measure or calculate the concentrations of reactants and products at equilibrium. All well and good, but is this simply an empirical measurement? It was certainly discovered empirically and has proven to be applicable to huge numbers of reactant systems. It just does not seem very satisfying to say this is the way things are without an explanation for why the equilibrium constant is constant. How does it relate to molecular structure? What determines the equilibrium constant? What is the driving force that moves a reaction towards equilibrium and then inhibits any further progress towards products?
You will remember (we hope) that it is the second law of thermodynamics that tells us about the probability of a process occurring. The criterion for a reaction proceeding is that the total entropy of the universe must increase. We also learned that we can substitute the Gibb’s free energy change (ΔG) for the entropy change of the universe, and that ΔG is much easier to relate to and calculate because it only pertains to the system. So it should not be a surprise to you that there is a relationship between the drive towards equilibrium and the Gibbs free energy change in a reaction. We have already seen that a large, negative Gibbs free energy change (from reactants to products) indicates that a process will occur (or be spontaneous, in thermodynamic terms[17]), whereas a large, positive equilibrium constant means that the reaction mixture will contain mostly products at equilibrium.
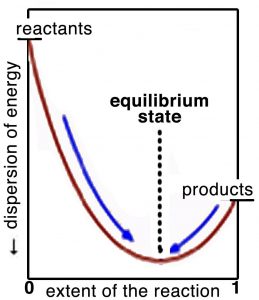 Think about it this way: the position of equilibrium is where the maximum entropy change of the universe is found. On either side of this position, the entropy change is negative and therefore the reaction is unlikely. If we plot the extent of the reaction versus the dispersion of energy (in the universe) or the free energy, as shown in the graph, we can better see what is meant by this. At equilibrium, the system sits at the bottom of an energy well (or at least a local energy minimum) where a move in either direction will lead to an increase in Gibbs energy (and a corresponding decrease in entropy). Remember that even though at the macroscopic level the system seems to be at rest, at the molecular level reactions are still occurring. At equilibrium, the difference in Gibbs free energy, ΔG, between the reactants and products is zero. It bears repeating: the criterion for chemical equilibrium is that ΔG = 0 for the reactants ⇄ products reaction. This is also true for any phase change. For example, at 100 ºC and 1 atmosphere pressure, the difference in free energy for H2O(g) and H2O(l) is zero. Because any system will naturally tend to this equilibrium condition, a system away from equilibrium can be harnessed to do work to drive some other non-favorable reaction or system away from equilibrium. On the other hand, a system at equilibrium cannot do work, as we will examine in greater detail.
Think about it this way: the position of equilibrium is where the maximum entropy change of the universe is found. On either side of this position, the entropy change is negative and therefore the reaction is unlikely. If we plot the extent of the reaction versus the dispersion of energy (in the universe) or the free energy, as shown in the graph, we can better see what is meant by this. At equilibrium, the system sits at the bottom of an energy well (or at least a local energy minimum) where a move in either direction will lead to an increase in Gibbs energy (and a corresponding decrease in entropy). Remember that even though at the macroscopic level the system seems to be at rest, at the molecular level reactions are still occurring. At equilibrium, the difference in Gibbs free energy, ΔG, between the reactants and products is zero. It bears repeating: the criterion for chemical equilibrium is that ΔG = 0 for the reactants ⇄ products reaction. This is also true for any phase change. For example, at 100 ºC and 1 atmosphere pressure, the difference in free energy for H2O(g) and H2O(l) is zero. Because any system will naturally tend to this equilibrium condition, a system away from equilibrium can be harnessed to do work to drive some other non-favorable reaction or system away from equilibrium. On the other hand, a system at equilibrium cannot do work, as we will examine in greater detail.
The relationship between the standard free energy change and the equilibrium constant is given by the equation:
ΔGº = – RT ln K
which can be converted into the equation
ln Keq= – ΔGº/RT or Keq= e –ΔGº/RT.
As we saw earlier, the superscript º refers to thermodynamic quantities that are measured and calculated at standard states. In this case ΔGº refers to 1 atmosphere pressure and 298 K and (critical for our present discussion) 1 M concentrations for both reactants and products. That is,: ΔGº tells you about the free energy change if all the substances in the reacting system were mixed with initial concentrations of 1.0 M. It allows us to calculate equilibrium constants from tables of free energy values (see Chapter 9). Of course, this is a rather artificial situation and you might be tempted to think that ΔGº is not very useful in the real world where initial concentrations of both reactants and products are rarely 1.0 M. But no, ΔGº does tell us something useful: it tells us which way a reaction will proceed under these starting conditions. If we have a specific set of conditions, we can use ΔGº to calculate the actual free energy change ΔG, where:
ΔG = ΔGº + RT ln Q
In this equation, the variable Q is called the reaction quotient. It has the same form as Keq([products]/[reactants], except that the concentrations are not 1.0 M. Rather, they are the actual concentrations at the point in the reaction that we are interested in. The sign and magnitude of ΔG then will tell us which way the reaction will proceed and how far in that direction it will go.
The differences between Q and Keq, ΔG, and ΔGº are important to keep in mind. It is easy to get mixed up and apply them incorrectly. Q and ΔG relate to non-equilibrium systems whereas Keq and ΔGº tell us about the equilibrium state itself. At equilibrium, Q = Keq, and ΔG = 0, so that the equation ΔG = ΔGº +RT ln Q becomes ΔGº = – RT ln Keq. Note that Keq and ΔGº are constant for a given reaction at a given temperature, but Q and ΔG are not; their values vary according to the reaction conditions. In fact, by using Q and/or ΔG, we can predict how a system will behave under a specific condition as it moves towards the highest entropy state (to where ΔG=0).
Equilibrium and Non-Equilibrium States
Let us look at a chemical system macroscopically. If we consider a reaction system that begins to change when the reactants are mixed up (that is, it occurs spontaneously), we will eventually see that the change slows down and then stops. It would not be unreasonable to think that the system is static and assume that the molecules in the system are stable and no longer reacting. However, as we discussed earlier, at the molecular level we see that the system is still changing and the molecules of reactants and products are still reacting in both the forwards and reverse reactions. In the case of our acetic acid example, there are still molecules of acetic acid, (AcOH), acetate (AcO–), and hydronium ion (H3O+) colliding with solvent water molecules and each other. Some of these reactions will have enough energy to be productive; molecules of acetate will transfer protons to water molecules and the reverse reaction will also occur. What has changed is that the rate of acetate (AcO–) and hydronium ion (H3O+) formation is equal and opposite to the rate of acetic acid deprotonation (transfer of the proton to water). Although there is no net change at the macroscopic level, things are happening at the molecular level. Bonds are breaking and forming. This is the dynamic equilibrium we discussed earlier.
Now what happens when we disturb the system. At equilibrium, the acetic acid–water system contains acetic acid (AcOH), protons (H3O+), and acetate ion (AcO–). We know that a 0.10-M solution of acetic acid has concentrations of [H3O+] = [AcO–] = 1.3 x 10–3 M. Now we add enough acetate[18] to make the acetate concentration 0.10 M? One way to think about this new situation is to consider the probabilities of the forward and backward reactions. If we add more product (acetate), the rate of the backward reaction must increase (because there are more acetate ions around to collide with). Note that to do this, the acetate must react with the hydronium ion, so we predict that the [H3O+] will decrease and the acetate will increase. But as we saw previously, as soon as more acetic acid is formed, the probability of the forward reaction increases and a new equilibrium position is established, where the rate of the forward reactions equal the rate of the backward reactions. Using this argument we might expect that at the new equilibrium position there will be more acetic acid, more acetate, and less hydronium ion than there was originally. We predict that the position of equilibrium will shift backwards towards acetic acid.
This probability argument gives us an idea of what will happen when an reaction at equilibrium is disturbed, but it doesn’t tell us exactly where it will restabilize. For that we have to look at Q and Keq. If we take the new initial reaction conditions (0.10 M AcOH, 0.10 M AcO–, and 1.3 x 10–3 M H3O+) and analyze them to determine the concentrations of all participating species, we can calculate Q and compare it to Keq:
Q = [H3O+][AcO–]/[AcOH] = (1.3 x 10–3)(0.1)/(0.1)
This generates a value for Q as 1.3 x 10–3. Now, if we compare Q and Keq, we see that Q is larger than Keq (1.3 x 10–3 > 1.8 x 10–5). To re-establish equilibrium, the system will have to shift so that Q becomes smaller or equal to Keq (at which point ΔG = 0). To do this, the numerator (products) must decrease, while the denominator (reactants) must increase.[19] In other words, the reaction must go backwards in order to reestablish an equilibrium state. This approach leads us to the same conclusion as our earlier probability argument.
If we recalculate the [H3O+] under the new equilibrium conditions (that is 0.10 M AcOH and 0.10 M acetate), we find that it has decreased considerably from its initial value of 1.3 x 10–3, down to the new value of 1.8 x 10–5 M.[20] Using this to calculate the pH, we discover that addition of sodium acetate causes the pH to rise from 2.9 to 4.5. This may not seem like much, but remember that each pH unit is a factor of 10, so this rise in pH actually indicates a drop in hydronium ion concentration of a bit less than a hundredfold. In order to regain the most stable situation, the system shifts to the left, thereby reducing the amount of product:
AcOH + H2O ⇄ H3O+ + AcO–
There are a number of exercises that will allow you to better understand the calculations involved in defining the effects of perturbations (changes in conditions, concentrations, and temperature) on the equilibrium state of a system. (Many chemistry books are full of such buffer and pH problems.) What is really important to note is that a system will return to equilibrium upon perturbation. This is where the system is most stable. And once the system is at equilibrium, further perturbations will lead to a new equilibrium state.
Le Chatelier’s Principle
You may recognize the preceding discussion as a rather well-known idea articulated by Henry Louis Le Chatelier: “If a chemical system at equilibrium experiences a change in concentration, temperature, volume, or partial pressure, then the equilibrium shifts to counteract the imposed change and a new equilibrium is established.” Le Chatelier’s principle is one of the best-known and most widely applicable heuristics (a rule of thumb that helps you predict an outcome) in science. However, it is important to understand why this principle works. Le Chatelier’s principle is yet another reminder that the second law of thermodynamics is always in force.
Le Chatelier’s principle specifically mentions different kinds of changes that can affect the position of equilibrium, yet we have only discussed changes in concentrations. What about temperature, volume, and partial pressure? How do they affect equilibrium? We have also not specifically addressed equilibrium reactions that take place in the gas phase. As an example, important atmospheric reactions such as the formation and depletion of ozone take place in the gas phase. There is nothing particularly special or different about calculating the equilibrium constant for gas phase reactions. We can use either partial pressures of each gas or concentrations (mol/L), although the value of Keq differs depending on which units you choose. Also, you can’t mix and match; you must use either all pressures or all concentrations. The effect of increasing the volume is the same as decreasing the concentration, and increasing the pressure has the same effect as increasing the concentration. Note, however, that adding a gas that is not a participant in the reaction has no effect even though the total pressure is increased.
Temperature, Equilibrium, and Reaction Rates
The effect of changing the temperature on the position of equilibrium is a little more complex. At first guess, you might predict that increasing the temperature will affect the rates of both the forward and backward reactions equally. However, if we look more closely, we see that this is not true. Cast your mind back to the discussions of temperature and thermal energy. If the temperature of the system is raised, it means that thermal energy has been added to the system from the surroundings. We can treat the addition of energy to the system as a perturbation and according to Le Chatelier’s principle, if something in the system is changed (concentration, volume, pressure, temperature), then the system shifts to a new equilibrium state. In order to predict the effect of adding energy to the system, we need to have more information about the energy changes associated with that system. As we saw earlier, the enthalpy change (ΔH) tells us about the thermal energy change for systems under constant pressure (most of the systems we are interested in). We can measure or calculate enthalpy changes for many reactions and therefore use them to predict the effect of increasing the temperature (adding thermal energy). For example, take the reaction of nitrogen and hydrogen to form ammonia.[21] This reaction is:
N2 (g) + 3 H2 (g) ⇄ 2 NH3 (g) (ΔH = -92.4 kJ/mol)
The reaction is exothermic because for each mole of ammonia (17g), 92.4 kJ of thermal energy is produced and transferred to the surroundings (as indicated by the negative sign of the enthalpy change). Now, if we heat this reaction up, what will happen to the position of equilibrium? Let us rewrite the equation to show that thermal energy is produced:
N2 (g) + 3 H2 (g) ⇄ 2 NH3 (g) + 184.8 kJ
(2 x 92.4 kJ since two moles of ammonia are produced). If thermal energy is a product of the reaction, Le Chatelier’s principle tells us that if we add more product, the reaction should shift towards the reactants. Sure enough, if we heat this reaction up, the position of equilibrium shifts towards ammonia and hydrogen—it starts to go backward! This is actually quite a problem, as this reaction requires a fairly high temperature to make it go in the first place. The production of ammonia is difficult if heating up the reaction makes it go in the opposite direction to the one you want.
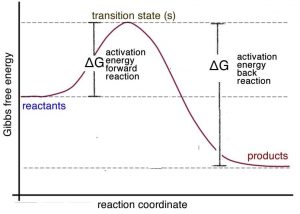
It is important to remember that Le Chatelier’s principle is only a heuristic; it doesn’t tell us why the system shifts to the left. To answer this question, let us consider the energy profile for an exothermic reaction. We can see from the graph → that the activation energy for the reverse (or back) reaction (ΔG≠reverse) is larger than that for the forward reaction (ΔG≠forward). Stated in another way: more energy is required for molecules to react so that the reverse (back) reaction occurs than for the forward reaction. Therefore, it makes sense that if you supply more energy, the reverse reaction is affected more than the forward reaction.[22]
There is an important difference between disturbing a reaction at equilibrium by changing concentrations of reactants or products, and changing the temperature. When we change the concentrations, the concentrations of all the reactants and products change as the reaction moves towards equilibrium again, but the equilibrium constant stays constant and does not change. However, if we change the temperature, the equilibrium constant changes in value, in a direction that can be predicted by Le Chatelier’s principle.
Equilibrium and Steady State
Now here is an interesting point: imagine a situation in which reactants and products are continually being added to and removed from a system. Such systems are described as open systems, meaning that matter and energy are able to enter or leave them. Open systems are never at equilibrium. Assuming that the changes to the system occur on a time scale that is faster than the rate at which the system returns to equilibrium following a perturbation, the system could well be stable. Such stable, non-equilibrium systems are referred as steady state systems. Think about a cup with a hole in it being filled from a tap. If the rate at which water flows into the cup is equal to the rate at which it flows out, the level of water in the cup would stay the same, even though water would constantly be added to and leave the system (the cup). Living organisms are examples of steady state systems; they are open systems, with energy and matter entering and leaving. However, most equilibrium systems studied in chemistry (at least those discussed in introductory texts) are closed, which means that neither energy nor matter can enter or leave the system.

In addition, biological systems are characterized by the fact that there are multiple reactions occurring simultaneously and that a number of these reactions share components—the products of one reaction are the reactants in other reactions. We call this a system of coupled reactions. Such systems can produce quite complex behaviors (as we’ll explore further in Chapter 9). An interesting coupled-reaction system (aside from life itself) is the Belousov–Zhabotinsky (BZ) reaction in which cesium catalyzes the oxidation and bromination of malonic acid.[23] If the system is not stirred, this reaction can produce quite complex and dynamic spatial patterns, as shown in the figure. The typical BZ reaction involves a closed system, so it will eventually reach a boring (macroscopically-static) equilibrium state. The open nature of biological systems means that complex behaviors do not have to stop; they continue over very long periods of time. The cell theory of life (the theory that all cells are derived from preexisting cells and that all organisms are built from cells or their products), along with the fossil record, indicates that the non-equilibrium system of coupled chemical reactions that has given rise to all organisms has persisted, uninterrupted, for at least ~3.5 billion years (a very complex foundation for something as fragile as life).
The steady state systems found in organisms display two extremely important properties: they are adaptive and homeostatic. This means that they can change in response to various stimuli (adaptation) and that they tend to return to their original state following a perturbation (homeostasis). Both are distinct from Le Chatelier’s principle in that they are not passive; they are active processes requiring energy. Adaptation and homeostasis may seem contradictory, but in fact they work together to keep organisms alive and able to adapt to changing conditions.[24] Even the simplest organisms are characterized by great complexity because of the interconnected and evolved nature of their adaptive and homeostatic systems.
Questions
Questions to Answer
- What does it mean when we say a reaction has reached equilibrium?
- What does the magnitude of the equilibrium constant imply about the extent to which acetic acid ionizes in water?
- Write out the equilibrium constant for the reaction H3O+ + AcO– ⇄ AcOH + H2O.
- What would be the value of this equilibrium constant? Does it make sense in terms of what you know about acid-base reactions?
- If the pH of a 0.15-M solution of an acid is 3.6, what is the equilibrium constant Ka for this acid? Is the acid a weak or strong acid? How do you know?
- Calcium carbonate (CaCO3) is not (very) soluble in water. Write out the equation for the dissolution of CaCO3. What would be the expression for its Keq? (Hint: recall pure solids and liquids do not appear in the expression.) If Keq for this process is 6.0×10-9, what is the solubility of CaCO3 in mol/L?
- What factors determine the equilibrium concentrations for a reaction?
- For the reaction N2 (g) + 3 H2 (g) ⇄ 2 NH3 (g) (ΔH = -92.4 kJ/mol), predict the effect on the position of equilibrium, and on the concentrations of all the species in the system, if you:
- add nitrogen
- remove hydrogen
- add ammonia
- heat the reaction up
- cool it down
- Draw a reaction energy diagram in which the reverse reaction is much faster than the forward reaction (and vice versa).
- As a system moves towards equilibrium, what is the sign of ΔG? As it moves away from equilibrium, what is the sign of ΔG?
- Explain in your own words the difference between ΔGº and ΔG.
- Imagine you have a reaction system A ⇌ B for which Keq = 1. Draw a graph of how ΔG changes as the relative amounts of [A] and [B] change.
- What would this graph look like if Keq = 0.1? or Keq= 2?
- If ΔGº is large and positive, what does this mean for the value of Keq?
- What if ΔGº is large and negative, how does the influence Keq?
Questions for Later
- Why is Keq temperature-dependent?
- Explain mechanistically why random deviations from equilibrium are reversed.
- If the value of Q is > Keq, what does that tell you about the system? What if Q is < Keq?
Questions to Ponder
- The acid dissociation constant for ethanol (CH3CH2OH) is ~10–15. Why do you think acetic acid is 10 billion times more acidic than ethanol? (Hint: draw out the structures and think about the stability of the conjugate base.)
- If ΔG for a system is = 0, what does that mean?
8.6 Back to Reaction Mechanisms
Recall that one of the most important reasons for studying reaction kinetics is to get information about the reaction pathway, or mechanism. Now that we have all the concepts we need to understand these ideas, let us go back and see how to put it all together. The rate equation, along with the equilibrium constant, is the key to unraveling what happens during a reaction.
We have seen that, at a given temperature, the reaction rate depends on the magnitude of the rate constant and the concentrations of one or more of the reactants. However, for the two seemingly similar substitution reactions we discussed earlier, the rate equations are different. What is going on here? The answer lies in the fact that most reactions do not occur in one step. In many cases, there is not a smooth transition from reactants to products with a single transition state and activation energy, as we have simplistically portrayed it. Rather, there are a series of steps, each with their own transition state and activation energy. Here, we will only consider one-step and two-step reactions, but in reality there could be many distinct steps from reactant to product. Each step represents a kind of sub-reaction, each with its own activation energy and equilibrium state. The kinetics of a reaction is generally determined by the slowest of these sub-reactions, whereby a kind of bottleneck or rate-limiting step is formed. The rate equation gives us information about what reactants are present in the rate-determining step of the reaction. The reaction can only go as fast as the slowest step (the step with the highest activation energy barrier). As an analogy, imagine you are traveling at 70 mph on a five-lane highway. If the lanes suddenly narrow to allow only one lane of traffic, all the cars slow down. Although they are capable of traveling faster, no one can get past the slowest cars.
The reaction we discussed earlier between methyl bromide (CH3Br) and hydroxide (–OH):
CH3Br + –OH + Na+ ⇄ CH3OH + Br– + Na+
has been shown experimentally to have the rate equation: rate = k [CH3Br] [–OH]
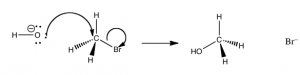
What this tells us that the rate of this reaction depends on both reactants. This means that whatever the mechanism of the reaction, both reactants must be present in the transition state (the species at the highest energy on the energy profile) that determines the rate of reaction. From this information we might begin to think about what the pathway for the reaction might be. It turns out that the simplest possibility is actually the correct – which is that the reaction takes place in one step, as shown in the figure. that is the hydroxide (the nucleophile) is attracted to the carbon, and at the same time the carbon bromine bond is broken. that is the reaction take place in one step that involves both the hydroxide and the methyl bromide.
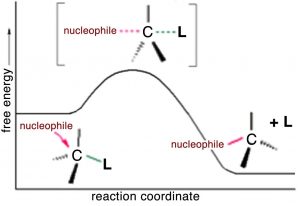
We can imagine what the structure of the transition state might look like (although we cannot detect it by any traditional methods because transition states only exist for one molecular vibration and are very difficult to detect). The nucleophile (–OH) is attracted to the δ+ on the methyl carbon. At the same time, the bromide ion starts to leave, so that at the “top” of the transition state (the most unstable point, requiring the most energy to form), we have a carbon that is coordinated to five other atoms by partial or full bonds. Given that carbon normally makes four bonds, it is no wonder that this pentavalent species sits at the reaction’s highest energy point.
However, if we analyze what appears to be a very similar reaction:
(CH3)3CBr + –OH ⇄ (CH3)3COH + Br.
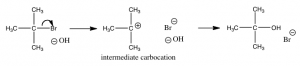 We must come to the conclusion that it has a different mechanism. Why? Because the rate equation for this reaction is first order: rate = k[(CH3)3CBr]. This tells us that only (CH3)3CBr is involved in the step that determines the rate. In other words, the transition state with the largest activation energy involves only the t-butyl bromide molecule. There is no nucleophile (the hydroxide) present during the step that determines how fast the reaction goes.
We must come to the conclusion that it has a different mechanism. Why? Because the rate equation for this reaction is first order: rate = k[(CH3)3CBr]. This tells us that only (CH3)3CBr is involved in the step that determines the rate. In other words, the transition state with the largest activation energy involves only the t-butyl bromide molecule. There is no nucleophile (the hydroxide) present during the step that determines how fast the reaction goes.
While there are a number of possible mechanism that we could postulate for this reaction, the mechanism for this reaction involves two discrete steps, as shown in the figure.
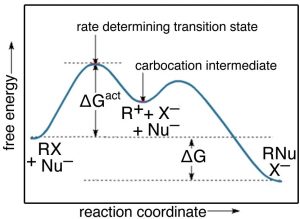
The first is the ionization of the t-butyl bromide, which involves breaking the C—Br bond. This results in a positively-charged carbon (the bromine takes all the electrons and becomes bromide ion)—a very unstable and distinct species known as a carbocation. The resulting carbocation is an intermediate: it sits in an energy well between two less stable states. This distinguishes it from the transition state, which precariously sits at the highest local energy state (surrounded by lower energy states). Intermediates lie in energy “valleys”, while transition states are at the summit of an energy “hill”, as shown in the figure. The carbocation can react with the hydroxide, to form the t-butyl alcohol, or it can react with the bromide to reform the original product (or a variety of other side reactions can occur). The important point here is that we can deduce how the reaction will proceed from the rate equation for each reaction.
Questions
Questions to Answer
- Draw a reaction energy diagram for a two-step reaction in which the second (or first) step is rate determining.
- What is the rate equation for a reaction which occurs in the following steps:
- A + B → C (fast)?
- A + C → D (slow)?
- Explain why it is not possible to write a rate equation from the reaction equation.
In this chapter we have explored how the fate of reactions is determined by a variety of factors, including the concentrations of reactants and products, the temperature, and the Gibbs energy change. We have learned that we can make a reaction go backward, forward, faster, or slower by examining the nature of the reaction and the conditions under which it is performed. You can now extend these principles to imagine how we might control reactions to do what we want, rather than let nature (or entropy) take its course. In the next chapter, we will take this one step further to see what happens when reactions are removed from isolation and allowed to interact with each other.
- The rate of reaction is discussed in the next section. ↵
- Recall that the pH = – log [H+], so [H+] = 10-pH , if the pH is = 1 then the concentration of H+ = 10–1, or 0.1 M. ↵
- We write acetic acid in this condensed formula for clarity, remembering that the actual structure of acetic acid is CH3C=O(O-H), and it is the H on the terminal O that is donated to a base (water). ↵
- This is true provided that we are talking about reasonably large numbers of molecules - the smaller the number of molecules, the “noisier” the process. You can think about the molecular movements of a single molecule compared to the movement of many molecules, as an example. ↵
- One very unfortunate consequence of this is that flour stored in grain silos can explode without warning, if exposed to a spark or other energy source. http://en.wikipedia.org/wiki/Grain_elevator#Elevator_explosions ↵
- The slope of the tangent is the change in concentration/change in time or the rate of the reaction. The slope of the tangent is the derivative of the curve at that point (calculus!). ↵
- You might ask yourself: How do we know the molecules are still reacting if we can only observe the macroscopic level? There are a number of ways of tracking what happens at the molecular level. For example, there are spectroscopic techniques such as NMR that can be used, but they are beyond the scope of this book. ↵
- In fact, this reaction has a number of different products. For now we will concentrate on this one. ↵
- We call these kinds of reactions substitution reactions because one group has been substituted for another. In fact, they are also nucleophilic substitution reactions, because the hydroxide is acting as a nucleophile here. ↵
- It is not necessary to be able to follow this mathematical reasoning; it is included to show where the equation comes from. ↵
- http://en.wikipedia.org/wiki/Spontaneous_human_combustion ↵
- R is known as the gas constant; it turns up in many different equations. For example, the ideal gas law PV=nRT (the units depend on the equation where it is used). R is also related to the Boltzmann constant kB, (or k, yet another confusing use of symbols, since the Boltzmann constant is in no way related to the rate constant (k), or the equilibrium constant (K)). ↵
- http://www.ncbi.nlm.nih.gov/pubmed/21332126 ↵
- Here is an example: http://www.febsletters.org/article/S0014-5793(07)00971-4/abstract ↵
- http://www.webmd.com/diet/features/trans-fats-science-and-risks ↵
- Strictly speaking, it is not concentrations that appear in the expression for K. Rather, it is another property called the activity (a)—often called the effective concentration. The activity takes into account the interactions between molecules and ions and solvents, but for our purposes it is acceptable to use concentrations in the expressions for Keq. One outcome of this is that activity is a dimensionless quantity, so equilibrium constants are one of the few places where we don’t have to worry about getting the right units! ↵
- Once more it is important to note that in thermodynamic terms, reactions referred to as spontaneous (inappropriately, in our view) do not indicate the rate at which a reaction will happen, but rather whether it will ever happen. In fact some “Spontaneous” reactions either do not occur at all (wood in an atmosphere containing oxygen does not burn spontaneously) or occur quite slowly (iron rusting). ↵
- Of course, there is no such thing as acetate (CH3COO–) alone. There must also be a counter-ion present. Typically, we use ions such as Na+ or K+, stable monovalent cations that will not participate in any further reaction. So when we say we add acetate to the solution, we really mean we add sodium acetate—the sodium salt of acetic acid (just like sodium chloride is the sodium salt of hydrochloric acid). ↵
- If you think about it for a moment you will see that if the concentration of any species changes in a closed system, then the concentrations of all the other species must also change. ↵
- You might be wondering if there is some trick here. There is—we are ignoring several side reactions that in fact tend to cancel each other out. If you are interested, there are a number of helpful sites that can assist you with the more complex calculations required. ↵
- The production of ammonia is a commercially-important process because nitrogen is an important element necessary for plant growth (it is commonly added to fertilizers). However, the major source of nitrogen is “locked up” in the air as molecular nitrogen, - a substance that is quite unreactive and inaccessible to most plants. ↵
- By analogy, consider the NCAA basketball tournament: if the field is widened to allow more participants, it helps the weaker teams because the stronger teams would have made it into the tournament anyway. ↵
- http://www.youtube.com/watch?v=IBa4kgXI4Cg ↵
- This type of adaptation is physiological and occurs within individual organisms; it is distinct from, but based on, evolutionary processes that act on populations of organisms. ↵

