3 Elements, Bonding, and Physical Properties
Melanie M. Cooper and Michael W. Klymkowsky

Up to now we have been concerned mainly with isolated atoms, an extremely abstract topic. We now move on to consider the macroscopic behavior of atoms, that is, the behaviors of very, very large numbers of atoms that form the materials that we touch, feel, smell, and observe with our own eyes. Before we do that, it is important to understand and be explicit about what properties atoms, molecules, and their aggregates can and cannot exhibit.
3.1 Elements and Bonding
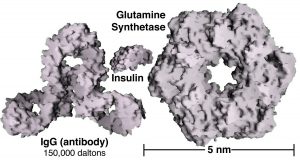
When atoms interact with one another to form molecules or larger structures, the molecules have different properties than their component atoms; they display what are often referred to as emergent properties, where the whole is more than, or different from the sum of its parts. In a similar way groups of atoms or molecules have different properties from isolated atoms/molecules. For example while groups of atoms/molecules exist in solid, liquid, or gaseous states, and often have distinct colors and other properties, isolated atoms/molecules do not; there are no solid or liquid isolated atoms and they do not have a color or a boiling point. So the obvious question is, how many atoms or molecules need to aggregate before they display these emergent properties, before they have a color, before they have a melting point, boiling point, heat capacity, and other properties that isolated atoms do not? The answer is not completely simple, as you are probably slowly coming to expect. As we add more and more atoms or molecules together their properties change but not all at once. You have probably heard about nanoscience and nanotechnologies, which have been the focus of a great deal of research and economic interest in the past decade or so. Nanoparticles are generally classified as being between 1 and 100 nm in diameter (a nanometer is one billionth of a meter or 1 x 10–9 m). Such particles often have properties that are different from those of bulk (macroscopic) materials. Nanomaterials can be thought of as a bridge between the atomic-molecular and macroscopic scales.

Assuming that they are pure, macroscopic materials have predictable properties and it doesn’t really matter the size of the sample. A macroscopic sample of pure gold behaves the same regardless of its size and if Archimedes (ca. 287–212 bce) were alive today, he could tell you whether it was pure or not based on its properties, for example, its density. But gold nanoparticles have different properties depending upon their exact size. For example, when suspended in water, they produce colors ranging from orange to purple, depending on their diameter (see Figure). Often the differences in the properties displayed are due to differences in the ratio of surface area to volume, which implies that intermolecular forces (forces between molecules) are more important for nanomaterials. As we cluster more and more particles together, the properties of the particles change. Biomolecules generally fall into the size range of nanomaterials, and as we will see their surface properties are very important in determining their behavior.
Unfortunately when we are talking about the properties of atoms and molecules versus substances and compounds, it can be difficult, even for experienced chemists, to keep the differences clear. In addition different representations are often used for different organizational levels; it is an important skill to be able to recognize and translate between levels. We will be using a range of representations to picture atoms and molecules; chemists (and we) typically use various shorthand rules, methods, and chemical equations to represent molecular composition, shape, and behaviors. But just knowing the equations, often the only thing learned in introductory chemistry courses, is not sufficient to understand chemistry and the behavior of atoms and molecules. Much of the information implied by even the simplest chemical equations can easily be missed—or misunderstood—if the reader does not also have a mental picture of what the diagram or equation represents, how a molecule is organized and its shape, and how it is reorganized during a particular reaction. We will be trying to help you get these broader pictures, which should you make sense of the diagrams and equations used here. That said, it is always important to try to explicitly identify what you are assuming when you approach a particular chemical system; that way you can go back and check whether your assumptions are correct.
Where Do Atoms Come From?
“We are stardust, we are golden, We are billion-year-old carbon.”
– Woodstock, Joni Mitchell“Sometimes I’ve believed as many as six impossible things before breakfast.”
– Alice in Wonderland, Lewis Carroll
Did you ever stop to ask yourself where the atoms in your body came from? Common answers might be that the atoms in our bodies come from food, water, or air. But these are not the ultimate answers, because we then need to ask, where did the atoms in food, water, and air come from? Where did the atoms in the Earth come from? There are really two general possibilities: either the atoms that make up the Earth and the rest of the universe are eternal or they were generated/created by some process. How do we decide which is true? What is the evidence favoring one model over the other? The answers come not from chemistry, but from astrophysics.
Given that we are thinking scientifically what kinds of evidence can we look for to decide whether atoms (or the universe) are eternal or recently created? Clearly we must be able to observe the evidence here and now and use it to formulate logical ideas that make clear and unambiguous predictions. As we will see we will be called upon once again to believe many apparently unbelievable things. The current organizing theory in astrophysics and cosmology, known as the Big Bang theory, holds that the universe is ~13,820,000,000 ± 120,000,000 years old or 13.82 ± 0.12 billion years – an unimaginable length of time. The Sun and Earth are ~5,000,000,000 years old, and the universe as a whole is ~156 billion light-years in diameter.[1]
The Big Bang theory was put forward in a response to the observation that galaxies in the universe appear to be moving away from one another. Because the galaxies that are further away from us are moving away more rapidly than those that are closer, it appears that space itself is expanding, another seriously weird idea.[2] Based on this observation, we can carry out what scientists call a thought experiment. What happens if we run time backwards, so that the universe is contracting rather than expanding? Taken to its logical conclusion, the universe would shrink until, at some point, all of the universe would be in a single place, at a single point, which would be unimaginably dense. Based on a range of astronomical measurements, this so-called singularity existed ~13.73 x 109 years ago, which means the universe is about 13.73 billion years old. The Big Bang theory tells us nothing about what happened before 13.73 x 109 years ago, and although there is no shortage of ideas, nothing scientific can be said about it, because it is theoretically unobservable, or at least that is what we have been led to believe by astrophysicists!
Thinking About Atomic Origins
The current model of the universe begins with a period of very rapid expansion, from what was essentially a dimensionless point, a process known as inflation. As you might well imagine there is some debate over exactly what was going on during the first 10-43 seconds (known as the Planck time) after the universe’s origin. Surprisingly, there is a remarkable level of agreement on what has happened since then.[3] This is because there is lots of observable evidence that makes it relatively easy to compare hypotheses, accepting some and ruling out others. Initially remarkably hot (about 1023 K), over time the temperature (local energy levels) of the universe dropped to those that are reachable in modern particle accelerators, so we have actual experimental evidence of how matter behaves under these conditions. At 1 picosecond after the Big Bang, there were no atoms, protons, or neutrons, because the temperature was simply too high. There were only elementary particles such as photons, quarks, and leptons (electrons are leptons) – particles that appear to have no substructure. By the time the universe was ~0.000001 seconds old (a microsecond or 1 x 10–6 second), the temperature had dropped sufficiently to allow quarks and gluons to form stable structures, and protons and neutrons appeared. A few minutes later the temperature dropped to about 1,000,000,000 K (1 x 109 K), which is low enough for some protons and neutrons to stick together and stay together without flying apart again. That is, the kinetic energy of the particles colliding with them was less than the forces (the weak and strong nuclear forces) holding the protons, neutrons, and nuclei together. At this point the density of particles in the universe was about that of our air.
By the time the universe was a few minutes old it contained mostly hydrogen (1H1 = one proton, no neutrons) and deuterium (2H1= one proton and one neutron) nuclei, with some helium (3He2 and 4He2 = two protons and either one or two neutrons, respectively), and a few lithium (7Li3 = three protons and four neutrons).[4] These nuclei are all formed by nuclear fusion reactions such as
1p+ + 1n0 → 2H+ + gamma radiation and 2H+ + 2H+ → 3He2+ + 1n0.
These fusion reactions take place in a temperature range where the nuclei have enough kinetic energy to overcome the electrostatic repulsion associated with the positively charged protons but less than that needed to disrupt the nuclei once formed. After a few minutes the temperature of the universe fell below ~10,000,000 (107) K. At these temperatures, the kinetic energy of protons and nuclei was no longer sufficient to overcome the electrostatic repulsion between their positive charges. The end result was that there was a short window of time following the Big Bang when a certain small set of nuclei (including 1H+, 2H+, 3He2+, 4He2+, and 7Li3+) could be formed. After ~400,000 years the temperature of the universe had dropped sufficiently for electrons to begin to associate in a stable manner with these nuclei and the first atoms (as opposed to bare nuclei) were formed. This early universe was made up of mostly (> 95%) hydrogen atoms with a small percentage each of deuterium, helium, and lithium, which is chemically not very interesting.
The primary evidence upon which these conclusions are based comes in the form of the cosmic microwave background radiation (CMBR), which is the faint glow of radiation that permeates the universe. The CMBR is almost perfectly uniform which means that no matter where you look in the sky the intensity of the CMBR is (essentially) the same. To explain the CMBR, scientists assume that the unimaginably hot and dense early universe consisted almost entirely of a plasma of hydrogen nuclei that produced vast amounts of electromagnetic radiation, meaning that the early universe glowed. The CMBR is what is left of this radiation, it is a relic of that early universe. As the universe expanded it cooled but those photons continued to whiz around. Now that they have to fill a much larger universe individual photons have less energy, although the total energy remains the same! The current background temperature of the universe is ~2.27 K, which corresponds to a radiation wavelength of ~1.9 mm (radiation in the microwave region); hence the name cosmic microwave background radiation.
After a billion years or so things began to heat up again literally (albeit locally). As in any randomly generated object the matter in the universe was not distributed in a perfectly uniform manner and as time passed this unevenness became more pronounced as the atoms began to be gravitationally attracted to each other. The more massive the initial aggregates the more matter was attracted to them. As the clumps of (primarily) hydrogen became denser the atoms banged into each other and these systems, protostars, began to heat up. At the same time the gravitational attraction resulting from the overall mass of the system caused the matter to condense into an even smaller volume and draw in more (mostly) hydrogen. As this matter condensed its temperature increased, as gravitational potential energy was converted into kinetic energy. At a temperature of ~10,000,000 (107) K the atoms (which had lost their electrons again because of the higher temperature) began to undergo nuclear fusion. At this point we would probably call such an aggregate of matter a star. This process of hydrogen fusion produced a range of new types of nuclei. Hydrogen fusion, or hydrogen burning as it is sometimes called, is exemplified by reactions such as the formation of helium nuclei:
4 1H+ → 4He2+ + 2e+ + energy.
When four protons are fused together they produce one helium-4 nucleus, containing two protons and two neutrons, plus two positrons (e+ – the antiparticle of the electron), and a great deal of energy. As the number of particles decreases (4 1H+ into 1 4He2+), the volume decreases. Gravity produces an increase in the density of the star (fewer particles in a smaller volume). The star’s core, where fusion occurs, gets smaller and smaller. The core does not usually collapse totally into a black hole, because the particles have a huge amount of kinetic energy, which keeps them in motion and moving on average away from one another.[5]
As the star’s inner temperature reaches ~108 K there is enough kinetic energy available to drive other fusion reactions. For example three helium nuclei could fuse to form a carbon nuclei:
3 4He2+ → 12C6+ + lots of energy (note again, the result is fewer atoms).
If the star is massive enough, a further collapse of its core would increase temperatures so that carbon nuclei could fuse, leading to a wide range of new types of nuclei, including those of elements up to iron (56Fe26+) and nickel (58Ni28+), as well as many of the most common elements found in living systems, such as nitrogen (Ni7), oxygen (O8), sodium (Na11), magnesium (Mg12), phosphorus (P15), sulfur (S16), chlorine (Cl17), potassium (K19), calcium (Ca20), manganese (Mn25), cobalt (Co27), copper (Cu29), and zinc (Zn30).
In some instances these nuclear reactions cause a rapid and catastrophic contraction of the star’s core followed by a vast explosion called a supernova. Supernovae can be observed today, often by amateur astronomers, in part because seeing one is a matter of luck. They are characterized by a sudden burst of electromagnetic radiation, as the supernova expels most of its matter into interstellar dust clouds. The huge energies involved in such stellar explosions are required to produce the naturally occurring elements heavier than iron and nickel, up to and including Uranium (Ur82+). The material from a supernova is ejected out into the interstellar regions, only to reform into new stars and planets and so begin the process all over. So the song is correct, many of the atoms in our bodies were produced by nuclear fusion reactions in the cores of stars that, at one point or another, must have blown up; we are literally stardust, except for the hydrogen formed before there were stars!
Looking at Stars
At this point you may still be unclear as to how we know all this. How can we know about processes and events that took place billions of years ago? Part of the answer lies in the fact that all the processes involved in the formation of new elements are still occurring today in the centers of stars. Our own Sun is an example of a fairly typical star; it is composed of ~74% (by mass) and ~92% (by volume) hydrogen, ~24% helium, and trace amounts of heavier elements. There are many other stars (billions) just like it. How do we know? Analysis of the emission spectra of the light emitted by the Sun or the light emitted from any other celestial object enables us to deduce which elements are present.[6] Similarly, we can deduce which elements and molecules are present in the clouds between stars by looking at which wavelengths of light are absorbed! Remember that emission/absorption spectra are a result of the interaction between the atoms of a particular element and electromagnetic radiation (light). They serve as a fingerprint of that element (or molecule). The spectrum of a star reveals which elements are present. No matter where an element is found in the universe it appears to have the same spectroscopic properties.
Astrophysicists have concluded that our Sun (Sol) is a third generation star, which means that the material in it has already been through two cycles of condensation and explosive redistribution. This conclusion is based on the fact that the Sun contains materials (heavy elements) that it could not have formed itself, and so must have been generated previously within larger and/or exploding stars. Various types of data indicate that the Sun and its planetary system were formed by the rapid collapse of a molecular (mostly hydrogen) cloud ~4.59 billion years ago. It is possible that this collapse was triggered by a shock wave from a nearby supernova. The gas condensed in response to gravitational attraction and the conservation of angular momentum; most of this gas (>98%) became the Sun, and the rest formed a flattened disc, known as a planetary nebulae. The planets were formed from this disc, with the small rocky/metallic planets closer to the Sun, gas giants further out, and remnants of the dust cloud distributed in the Oort cloud.[7] As we will see, living systems as we know them depend upon elements produced by second and third generation stars. This process of planet formation appears to be relatively common and more and more planetary systems are being discovered every year.[8]
Stars have a life cycle from birth to death; our Sun is currently about half way through this life cycle. There is not enough matter in the Sun for it to become a supernova, so when most of its hydrogen has undergone fusion, ~5 billion years from now, the Sun’s core will collapse and helium fusion will begin. This will lead to the formation of heavier elements. At this point, scientists predict that the Sun’s outer layer will expand and the Sun will be transformed into a red giant. Its radius will grow to be larger than the Earth’s current orbit. That will be it for life on Earth, although humans are likely to become extinct much sooner than that. Eventually the Sun will lose its outer layers of gas and they may become a part of other stars elsewhere in the galaxy. The remaining core will shrink, grow hotter and hotter, and eventually form a white dwarf star. Over (a very long) time, the Sun will cool down, stop emitting light, and fade away.
Questions
Questions to Answer
- How do the properties of isolated atoms or molecules give rise to the world we observe? Why are objects different colors, or have different melting points?
- Do isolated atoms/molecules exist in a state such as solid, liquid, or gas?
- Where do the atoms in your body come from? (Trace their origin back as far as you can.)
- How does the size of the universe influence the density of particles?
- How many protons, neutrons, and electrons does 4He have? How about 4He2+?
- Generate a graph that estimates the number of atoms in the universe as a function of time, beginning with the Big Bang and continuing up to the present day.
- Draw another graph to illustrate the number of elements in the universe as a function of time. Explain your reasoning behind both graphs.
Questions to Ponder
- Can an atom of one element change into an atom of another element?
- Is the number of atoms in the universe constant?
- How does the big bang theory constrain the time that life could have first arisen in the universe?
3.2 Elements and Their Interactions
“From the 115 elements you can build a near infinity of molecules, of any type you need, to get all the structural and functional diversity you can ask for. There are at least 100,000 different molecules in the human body. Some 900 volatile aroma components have been found in wine. Chemistry is molecules. We are molecules. Chemistry is a truly anthropic science.”
–Roald Hoffman (1937) quoted by Natalie Angier in The Canon
By this point, you probably have some idea or mental image of the basic (low resolution) structure of atoms. We will therefore return to some questions left unanswered at the end of Chapter 1. Why is it that two hydrogen atoms form a strong stable (covalent) bond, a bond that requires temperatures above 5000 K to break, whereas two helium atoms and two hydrogen molecules have only a weak (London dispersion forces) attraction for each other that is broken at very low temperatures (4–20 K)? Because temperature is a measure of the kinetic energy present in the system we have to ask, what gives rise to this huge difference? Is there something fundamentally different going on in these situations? Other potentially troubling questions may also come to mind, in particular, how can pure samples of different elements be so different? Why is carbon either black (graphite) or transparent (diamond)? Why is gold shiny and yellow, while sulfur is dull and yellow? Why are most metals, but not gold or copper, shiny, solid, and colorless, while mercury is shiny, colorless, and liquid? Why are some elements more or less inert (such as gold, which does not tarnish) while others, such as iron (which rusts) and phosphorus (which bursts into flames) are highly reactive? To answer these questions will lead to an understanding of the basics of chemistry or how atoms interact with one another under various conditions. We will approach the answers in a step-by-step manner. In some cases where the answers are very complex (as is the case for why gold is yellow and mercury is a liquid), we will sketch out the answer but probably not provide a satisfying explanation. Luckily, most of the chemistry we need to address is not nearly so arcane!
Before we consider these and other questions, let us recap what we think we know about atoms and electrons. Most of an atom’s mass is localized in a very small region, the nucleus, surrounded by electrons that occupy most of the volume of the atom. Electrons have a number of strange properties because they are quantum mechanical particles. This means that under some conditions their behavior is best described by considering them as negatively charged particles, and under other conditions it is more helpful to consider them as waves; they are really both (and neither). Because of the uncertainty principle when we know the energy of each electron rather accurately we do not (and cannot) know where, exactly, a particular electron is at a particular moment in time. In fact, because all electrons are identical, if we had two electrons and turned away from them we could not tell which was which when we turned back. Within an atom each electron has a discrete energy and is characterized by its set of quantum numbers; no two electrons in an atom have the same set of quantum numbers. Perhaps you will be disappointed (or perhaps pleased) to know that a rigorous quantum mechanical (and relativistic) treatment of atoms and their interactions is beyond the scope of this book.[9] That said, we can give a reasonable overview of how the behavior of atoms can be explained in terms of atomic and molecular electron orbitals. We will also indicate where our description is an over-simplification.
It is worth remembering that there are very few (if any) instances when we come across isolated atoms. Although we often describe matter as being composed of atoms, that is a bit of an abstraction; most atoms are stuck to other atoms by bonds and interactions. As mentioned previously, this leads to emergent properties that are quite distinct from those of the isolated atoms of which they are composed. It is the interactions between atoms and molecules that makes surfaces solid.
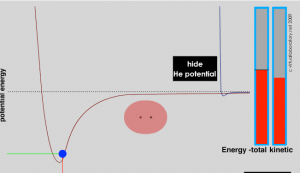
If isolated atoms are rare, the obvious question is, why are they rare? What determines when and how atoms interact? The answer is simple really and based on a principle we have already encountered (and that we will return to time and again): systems will adopt the lowest energy state accessible to them. The reason is that at the lowest accessible energy state, the forces of attraction and repulsion are equilibrated. It would take more energy to move the components of the system (that is atoms in molecules, or electrons in atoms) because the forces acting on them would increase. Interactions and bond formation lead to lower potential energy. Whether the bonded system is stable will then depend upon the strength of the interaction/bond and the forces that impact the molecule. For example, surrounding molecules/atoms with a range of kinetic energies may collide with the molecule. If this kinetic energy of the impacting particle is larger than the interaction/bond energy, the collision can disrupt the interaction or break the bond(s) between them; if not, the interaction/bond will be stable. At the same time, there must be overarching principles governing which interactions occur and which do not; otherwise everything would clump together, which would be messy and not particularly interesting. These principles arise from the way electrons are organized in different types of atoms.
Thinking about the nature of the chemical bond
There is no single explanation that captures all the properties observed when atoms interact to form a bond.[10] Instead we use a range of models of bonding. Now, what do we mean by model? Models are much more limited than theories, which have global application and can be proven wrong through observation and experimental data. Models are more like strategies that simplify working with and making predictions about complex systems. A model often applies to only very specific situations. For example the Bohr model of the atom applies only to hydrogen and then only under quite specific circumstances. We are going to consider a variety of bonding models, some of which you may already be familiar with, but it is important that you remember that different models are used depending upon which properties you want to predict and explain.
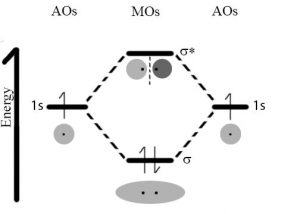
So back to our original dilemma, namely why is it that the interaction between two hydrogen atoms is so much stronger than that between two helium atoms? One useful model of bonding uses the idea that electrons can be described in terms of orbitals.[11] Each orbital can contain a maximum of two electrons (with opposite spins). Recall that in an isolated atom, the electrons are described by atomic orbitals; therefore when in molecules, they are described by molecular orbitals (MOs). When atoms approach each other, the atomic orbitals containing their outermost electrons, known as the valence electrons, begin to interact. Because of the wavelike nature of the electron, these interactions can be either constructive or destructive. If they interact in a constructive manner, the interaction is stabilizing, which means that potential energy decreases and (if that energy is released into the surrounding system) the two atoms adopt a more stable configuration; they form a bond that holds them together. If the interaction is destructive, there is no stabilizing interaction. In the case of hydrogen each atom has a single (1s) orbital occupied by a single electron. As the atoms approach one another these 1s atomic orbitals interact to form two possible MOs: a lower energy, constructive or bonding MO, and a higher energy, destructive or anti-bonding MO. Notice that the bonding MO, a so-called σ1s (sigma) orbital, has electron density (that is a high probability that the electrons would be found there if we looked) between the two hydrogen nuclei. In the anti-bonding MO, known as σ*1s, the electrons are mostly not between the nuclei. One way to think about this is that in the bonding orbital the protons in the hydrogen nuclei are attracting both electrons (one from each atom) and it is this common attractive force between electrons and nuclei that holds the two hydrogen atoms together. In contrast in the anti-bonding orbital there is little electron density between the two nuclei and any electrons in that orbital are actually destabilizing the system by enhancing the repulsive interactions between the nuclei. (Can you provide a short reason why this would be the case?)
Just like an atomic orbital each MO, both bonding and anti-bonding, can hold two electrons. In the case of two approaching hydrogens there are only two electrons present in the system and the lowest energy state would have them both in the bonding orbital. Typically, both electrons in a H–H molecule are found in the lower energy (more stable) σ1s bonding orbital. This arrangement of electrons is referred to as a covalent bond; this is the arrangement that requires temperatures of ~5000 K to break, which means it requires a lot of energy to break a covalent bond.
Now let us take a look at what happens when two helium atoms approach. Each He atom has two electrons in its 1s orbital. As the orbitals approach they interact and again produce two MOs, the bonding σ1s orbital and the anti-bonding σ*1s orbital. The σ*1s MO has no electron density between the two He nuclei and has considerably higher energy than the atomic orbitals of the isolated atoms. Since there are 4 electrons present in the two He atoms and only two can occupy the σ1s bonding orbital; the other two have to go into the σ*1s anti-bonding orbital. The end result is that the decrease in potential energy (increased stability) associated with occupying the bonding orbital is more than off-set by the increased energy associated with occupying the σ*1s anti-bonding orbital. So, the end result is no overall stabilization and no decrease in energy associated with bond formation; no covalent bond is formed. The only interactions between helium atoms are the van der Waals interactions that occur between the two atoms that depend exclusively on London dispersion forces, as discussed in Chapter 1.
The interaction between two helium atoms is very similar to that between two H2 molecules. There is no possibility of stabilizing MOs forming and, as in the case of the helium atoms, hydrogen molecules (H–H or H2) interact exclusively through London dispersion forces (LDFs). The LDFs will be somewhat stronger between hydrogen molecules than between helium atoms, however, because there is a larger surface area over which they can interact.
The idea that—all other things being equal—a system will move to the lowest accessible energy state (losing the excess energy to their surroundings), where the forces of attraction and repulsion are equal, is applicable to a wide range of situations. The potential energy of the system falls as the distance between the atoms decreases until the system reaches a balance between the stabilizing interaction of bond formation and the destabilizing repulsion of the two nuclei. The energy difference between the separated atoms and the minimum energy is called the bond energy and this amount of energy must be supplied to the system to break the two atoms apart again. The distance between the nuclei when the bond energy is at its minimum is the bond length. When a bond is formed between two atoms energy is always released to the surroundings and the new material is always more stable than the two separate atoms. Because energy is conserved a bond cannot form unless this bond energy is transferred from the interacting atoms to the rest of the system (usually by colliding with other atoms and transferring energy). Making bonds is always exothermic (meaning that energy is released not absorbed). This implies that energy (from the surrounding system) is always needed to break a bond. To break a bond energy must be transferred from the surroundings. Bond breaking is endothermic meaning it requires energy from the external world, normally delivered through collisions with other molecules.
When we consider more complex chemical reactions we will find that these generally involve both bond breaking and bond formation; the overall reaction will be exothermic when more energy is released from bond formation than is used for bond breaking. Conversely a reaction is endothermic (that is, uses energy) if more energy is required to break bonds than is released in bond formation. The important point is that we have to consider the system as a whole, including all of the bonds formed and broken. We will come back to this topic (in much greater depth) in Chapters 5 and 7.
Discrete Versus Continuous Molecules
Having considered the bonding situation with hydrogen and helium, the simplest two elements, we can now move on to consider other elements and the types of molecules that they form. In this discussion, we begin with molecules made up of a single type of atom. More complex molecules made of atoms of multiple elements will be considered in the next and subsequent chapters. As the number of protons in the nucleus of an element’s atoms increases, from 1 in hydrogen to 10 in neon, we find dramatic changes in physical properties that correlate with whether the elemental form is discrete or continuous. The discrete forms are either monoatomic—meaning that they exist as separate atoms (such as He and Ne) with no covalent bonds between them (although they do interact via van der Waals interactions)—or diatomic molecules (such as H2, N2, O2, and F2), meaning that they exist as molecules that have only two atoms. The elements that exist as small molecules have very low melting points (the temperatures at which they change from a solid to a liquid) and low boiling points (the temperatures at which they change from a liquid to a gas). But don’t confuse these phase transitions with the breaking of a diatomic molecule into separate atoms. Phase transitions, which we will discuss in greater detail later, involve disruption of interactions between molecules (intermolecular forces), such as London dispersion forces, rather than interactions within molecules, that is, covalent bonds.
Table 3.1 The First 10 Elements in Their Naturally Occurring Elemental State
| Elemental Form | H2
molecular |
He
atomic |
Li
continuous |
Be
continuous |
B
continuous |
C
continuous |
N2
molecular |
O2
molecular |
F2
molecular |
Ne
atomic |
| Melting Point | 13.81 K | 0.00 K | 453.65 K | 1560 K | 2348 K | 3823 K | 63.15 K | 54.36 K | 53.53 K | 24.56 K |
| Boiling Point | 20.28 K | 4.22 K | 1615 K | 2744 K | 4273 K | 4098 K | 77.36 K | 90.20 K | 85.03 K | 27.07 K |
| Bp-Mp (*) | 6.47 K | 3.27 K | 1161 K | 1184 K | 1925 K | 275 K | 14.21 K | 35.84 K | 31.5 K | 2.51 K |
| Name | hydrogen | helium | Lithium | beryllium | boron | carbon | nitrogen | oxygen | fluorine | neon |
* boiling point (Bp) minus melting point (Mp).
In contrast to the elements that form discrete molecules, the atoms of the other elements we are considering (that is Li, Be, B, C) interact with one another in a continuous manner. Rather than forming discrete molecules, these elements can form ensembles of atoms in which the number of atoms can range from the small (a few billion) to the astronomical (very, very large). Whether the materials are at the nano- or the macroscopic levels, the atoms in these ensembles are held together by bonds that are very difficult to break, like the bond in H–H. That is, a lot of energy must be put into the system to separate the component atoms. However, unlike hydrogen, the atoms that form these structures must form bonds with more than one other atom.
A consequence of this difference in organization is a dramatic increase in both the melting and boiling points compared to atomic (He, Ne) and molecular (H2, N2, O2, and F2) species (Table 3.1). The reason is that when a substance changes from solid to liquid (at the melting point) the component particles have to be able to move relative to one another. When the substance changes from a liquid to a gas (at the boiling point) the particles have to separate entirely. Consequently the magnitude of the melting and boiling points gives us a relative estimate of how strongly the particles are held together in the solid and liquid states. As we have already seen temperature is a measure of the average kinetic energy of the molecules in a system. For elements that exist as discrete atoms or molecules the only forces that are holding these particles together are London dispersion forces, which are relatively weak compared to covalent bonds. In contrast, the elements that exist as extensive networks of atoms joined by bonds require much more energy to break as the material goes from solid to liquid to gas.
Questions
Questions to ponder
- Are all bonds the same?
- What factors might influence bond strength?
- Why are the properties of atoms and molecules different?
Questions to Answer
- Where are the electrons in H2 when the temperature is greater than 5000 K?
- What would happen if you could form a He–He system with 3 electrons (instead of 4)?
- What would a molecular-level picture of H2 (g) look like?
- What would a molecular-level picture of H (g) look like?
- Where does the energy to break a bond come from?
- Where does the energy released upon bond formation go?
- The melting point of molecular hydrogen (H2) is ~14 K (-259 °C). Draw a molecular level picture of what molecular hydrogen looks like below this temperature (as a solid). Why are the molecules of hydrogen sticking together?
- The boiling point of molecular hydrogen (H2) is ~20 K (-253 °C). Draw a molecular level picture of what molecular hydrogen looks like above this temperature (as a gas).
- Molecular hydrogen dissociates at high temperatures (> 6000 K). Draw a picture of what you imagine this might look like. Why do you think it takes such a high temperature to bring about this change?
3.3 Carbon: An Amazingly Allotropic Element
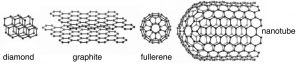
To give you an idea of some of the different types of bonds that form between elements, we are going to consider several representative elements from different areas of the periodic table. For starters, let us take a look at carbon. Carbon (C) belongs to the family of elements known as non-metals. The bonding between C atoms (and to other types of atoms) is typically described as covalent bonding where each bond involves two electrons (one from each of the bonded atoms). Although this is the most common model we will see that it is not the only possible one; we will introduce other models as they are needed. Diamond is the name given to one of the naturally occurring forms (known as allotropes) of pure C; the other allotropes of carbon are graphite, graphene, and various fullerenes (↓), which we will return to later. The important question is: How can these substances have such different properties, yet be composed of the same types of atoms? For example: diamond is hard, colorless, sparkly and do not conduct electricity, but graphite is soft, grey, shiny, and does conduct electricity. The answer lies in the molecular level structure of these allotropes of carbon.
Diamonds form from carbon-rich materials subjected to very high pressure (45,000–60,000 atmospheres) but relatively low temperatures (900–1300 ºC).[12] Such conditions can be found about 100 miles under the Earth’s crust, the region known as the lithosphere. Diamonds have also been found in asteroids, which originate from outside of the Earth. Diamonds are so valued because they are rare, sparkly, hard, and almost completely inert. It is very hard to make diamonds do anything at all except sit there and sparkle; they don’t dissolve in water and they melt only at very high temperatures (mp = 3330 °C). Diamond has the highest melting point of any known substance, so high that these measurements are actually done under high pressure and then calculated to estimate what the value would be at atmospheric pressure. In addition, when diamond is melted it decomposes. When it is heated in an atmosphere of oxygen it reacts to produce carbon dioxide; when oxygen is absent it transforms into graphite. There is no such thing as molten diamond. Diamonds are extremely hard (the hardest naturally occurring substance) and do not conduct electricity at all (as we will see, to conduct electricity, electrons must be able to flow through the material). This suggests that the molecular-level structure of diamond is quite different from that found in metals (which we will see are malleable and conduct electricity). Any useful model of diamond’s structure must explain how these properties arise from atomic interactions.
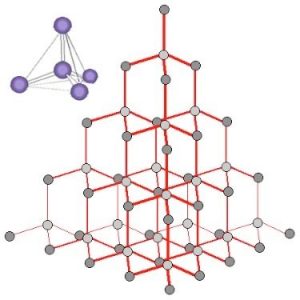
Let us step back and look at the properties of diamond and see if we can make sense of them. To be so stable (chemically inert) diamond must have very strong bonds that take a lot of energy to break. The fact that it does not conduct electricity indicates that the electrons must not be free to move around within a diamond. A polished diamond is sparkly because some light is reflected from the surface and some light passes through it, making it transparent. If the diamond were not cut with so many facets it would allow most light to pass through it.
When we look at an X-ray diffraction-based structure[13] of diamond we find that each carbon atom is surrounded by four other carbon atoms situated at equal distances and equal angles from each other. In this context, the most useful model of bonding involves thinking of each carbon atom as forming four covalent (electron-sharing) bonds, all arranged so that the electron pairs are as far apart as possible. This places the four bonded atoms at the corners of a tetrahedron, with a central carbon atom. Each of these corner atoms is itself at the center of a similar tetrahedron of carbons (see Figure). Experimental evidence indicates that all the bonds, bond lengths, and bond angles in diamond are identical; the C–C–C bond angles are ~109º. A diamond can be considered as one huge molecule connected by a network of carbon–carbon bonds.
How do we explain this arrangement in terms of what we know about the electronic structure of carbon atoms? The answer is that the electronic structure of the carbon atoms is reorganized to form bonding orbitals. In the case of carbon, each atom can form four bonding orbitals that are oriented as far apart as possible. There are several models to explain how this occurs, but it is important to remember that they are all models, designed to help us understand the properties of diamond.
The Hybrid Orbital Model
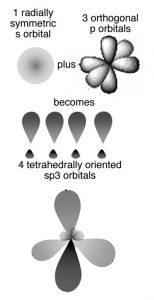
In this model the orbitals involved in carbon–carbon bonding are considered to be hybrids or mixtures of atomic orbitals. If carbon forms four bonds (and it does) then four bonding orbitals are needed. Carbon has available orbitals in the second (n = 2) quantum shell: the 2s, 2px, 2py, and 2pz In an isolated carbon atom there is a full 2s orbital and two half-filled p orbitals. When the carbon atoms form a bond, these orbitals are somehow mysteriously transformed into four new bonding orbitals, which are called sp3 hybrid orbitals because they are a mixture of an s and three p orbitals. These sp3 orbitals exist only in the context of bonded carbon; they are not present in isolated carbon atoms. They spring into existence when one carbon atom interacts with another atom to form a bond; they are generated through the interaction. In the case of carbon the four electron clouds (bonds) move as far apart as possible to minimize the repulsions between them, adopting a tetrahedral configuration (→).
The Molecular Orbital Model
Another way to consider how these bonds form is similar to the way we approached molecular hydrogen. That is, we consider that when carbon–carbon (C–C) bonds form, atomic orbitals are transformed into molecular orbitals (MOs). For each stabilizing bonding orbital, a destabilizing antibonding orbital is also formed. Using the molecular orbital approach, we can model the bonding in diamond as carbon atoms forming a three-dimensional network held together by these molecular bonding orbitals. C–C bonds are very stable because there is a large energy gap between the bonding orbitals and the high-energy antibonding orbitals. The bonding molecular orbitals are occupied while the antibonding molecular orbitals are unoccupied. Because of this large gap between the filled bonding and empty antibonding orbitals it is hard to remove an electron from a C–C bonding MO. The electrons are not free to move between energy levels. Given that electrical conduction depends upon the relatively free movement of electrons it is not surprising that diamonds do not conduct electricity. But why, you might ask, is a diamond transparent, rather than opaque, like a block of graphite, which is also composed of only carbon atoms? For an object to be transparent most of the light that hits it must pass through it; the light can be neither reflected or absorbed. For a diamond to absorb light a photon would need to move an electron from a low-energy bonding MO to a high-energy antibonding orbital. However, visible light does not have enough energy to bridge the energy gap between the bonding and antibonding orbitals. Based on this thinking we conclude that there is something different between bonds holding C atoms together in diamond from the bonds holding C atoms together in graphite even though we do not know, at this point, what it could be.
An important point to consider here is that we have described the bonding in carbon using two different models: the hybrid orbital (valence bond) and molecular orbital models. Although this may be (a bit!) confusing, and may take some getting used to, it is quite common to describe chemical and physical phenomena using different models. Typically we use the simplest model that will allow us to explain and predict the phenomenon we are interested in. Usually the bonding in carbon is described using the hybrid orbital model, because it is highly predictive and easier to use in practice.
Graphite
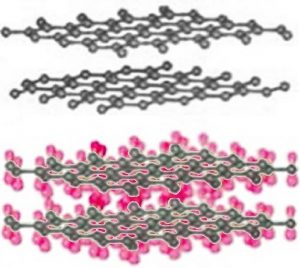
As we have already mentioned, different allotropes (different forms of the same element) can have quite different properties. The carbon allotrope graphite is soft, grey/black, opaque, conducts electricity, and slippery – it makes a good lubricant.[14] Diamond is hard, transparent, and does not conduct electricity. How can this be possible if both are pure carbon? The answer lies in how the carbon atoms are organized with respect to one another. Whereas the carbon atoms in diamond form a three-dimensional network, in graphite, the atoms are organized in two-dimensional sheets that stack one on top of the other. Within each two-dimensional sheet the carbon atoms are linked by covalent bonds in an extended array of six-membered rings. This means that the carbon sheets are very strongly bonded, but the interactions between sheets are much weaker. Although there are no covalent bonds between the sheets, the atoms of the sheets do interact through London dispersion forces, very much like the interactions that hold helium atoms together. Because the sheets interact over very much larger surface areas (→), however, these interactions are much stronger than those in helium. Yet another allotrope of carbon, graphene, consists of a single sheet of carbon atoms.[15] These sheets can be rolled into tubes to form nanotubes that are the subject of intense research interest because of their inherently high tensile strength. Carbon atoms can also form spherical molecules, known as buckminsterfullerenes or buckyballs.[16]
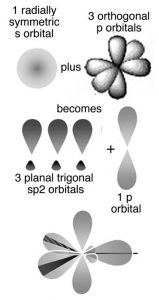
The obvious question is, why don’t covalent bonds form between graphite sheets? Why are the patterns of covalent bonding so different: three-dimensional (tetrahedral) in diamond, with each carbon bonded to four others, and two-dimensional (planar) in graphite and graphene, with each carbon atom bonded to only three others? One way to describe the molecular structure is to use the hybrid orbital bonding model. As we discussed previously, to form the four bonds attached to each carbon atom in diamond, we needed to hybridize four atomic orbitals to form four bonding orbitals. We might think we only need three bonds in graphite/graphene because each carbon is only connected to three others. This is not exactly true. In graphite and graphene we use a model in which only three atomic orbitals are hybridized—an s and two 2p orbitals in order to form three sp2 bonding orbitals. These orbitals attach each carbon atom to three other atoms. Just like in diamond the three bonds associated with each carbon atom in graphite/graphene move as far apart as possible to minimize electron pair repulsion; they lie at the points of a triangle (rather than a tetrahedron). This geometry is called trigonal planar and the C–C–C bond angle is 120° (→).
All well and good, but this does not really explain why the carbons in graphite/graphene are attached to three other carbon atoms, whereas in diamond each carbon is attached to four others. Perhaps surprisingly there is no good answer for why carbon takes up different forms—except that it can. But in fact carbon does form four bonds in graphite (carbon almost always forms four bonds—a central principle of organic chemistry). The trick is that the four bonds are not always equivalent; in graphite the fourth bond is not formed by the sp2 bonding orbitals but rather involves an unhybridized 2p atomic orbital. These p orbitals stick out at right angles to the sheet and can overlap with p orbitals from adjacent carbons in the same sheet (see Figure). Remember that p orbitals have two regions of electron density. To explain the fact that graphite conducts electricity, we use an idea from molecular orbital (MO) theory, namely that bonding and antibonding MOs are formed from the adjacent p orbitals that extend over the sheet surface. The energy different between these orbitals is not large and electrons can move from one to the other, allowing the movement of electrons throughout the whole sheet of graphite, which gives it many of the properties that we associate with metals. Note that we use both the hybridization model, which explains the planar framework of C–C bonds in graphite, and molecular orbital theory, which explains graphite’s electrical conductivity. So before we delve further into the properties associated with graphite, let us take a look at bonding in metals.
Questions
Questions to Answer
- Diamond and graphite appear to be quite different substances, yet both contain only carbon atoms. Why are the observable properties of diamond and graphite so different when they are made of the same substance?
- The electron configuration of C is 1s2 2s2 2p2. Using the idea that each atom provides one electron to a bond, if carbon used atomic orbitals to bond, how many bonds would it form? Would they all be the same? What would be the bond angles if this were to happen? (Draw a picture of what this might look like.)
- The electron configuration of C is 1s2 2s2 2p2 this means that carbon has 6 electrons. Why doesn’t it form 6 bonds?
- We have seen that carbon can form materials in which it bonds to 4 other atoms (sp3 hybridization) or three other atoms (sp2 hybridization). What would be the hybridization for a carbon that was only bonded to two atoms? How would the other (unhybridized) p orbitals influence the behavior of such material (assuming that it could form)?
Questions to Ponder
- Could carbon form a three-dimensional structure by linking to two other carbon atoms?
- Do you think diamonds are transparent to all forms of light, such as X-rays?
- What does the color of graphite imply about the energies of the photons it absorbs?
3.4 Metals
 Metals have quite a wide range of properties at normal temperatures, from liquid (like mercury) to extremely hard (like tungsten). Most are shiny but not all are colorless. For example gold and copper have distinct colors. All metals conduct electricity but not all equally. How can we explain all these properties? Let us use aluminum (Al) as an example because most of us have something made of aluminum such as a pan or aluminum foil. With modern instrumentation it is quite easy to visualize atoms and a variety of techniques have been used to image where the aluminum atoms are in the solid structure. What emerges is a picture of aluminum nuclei and their core electrons, packed like spheres where one layer of spheres rests in the interstices of the underlying and overlying layers; where the positions of the electrons are within this structure not well defined.
Metals have quite a wide range of properties at normal temperatures, from liquid (like mercury) to extremely hard (like tungsten). Most are shiny but not all are colorless. For example gold and copper have distinct colors. All metals conduct electricity but not all equally. How can we explain all these properties? Let us use aluminum (Al) as an example because most of us have something made of aluminum such as a pan or aluminum foil. With modern instrumentation it is quite easy to visualize atoms and a variety of techniques have been used to image where the aluminum atoms are in the solid structure. What emerges is a picture of aluminum nuclei and their core electrons, packed like spheres where one layer of spheres rests in the interstices of the underlying and overlying layers; where the positions of the electrons are within this structure not well defined.
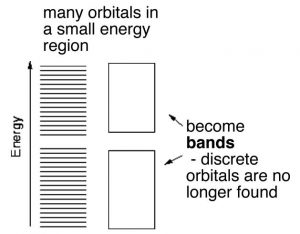
In H–H or diamond the electrons involved in bonding are located (most probably) between the two nuclei. In contrast in aluminum and other metals the valence electrons are not closely associated with each nucleus. Instead they are dispersed over the whole macroscopic piece of metal. Imagine that instead of two or three or four atomic orbitals combining to form MOs, a mole (6 x1023) of atomic orbitals were combined to produce a mole of MOs. As more and more MOs are formed the energies between them gets smaller and smaller. For a macroscopic piece of metal (one you can see) the energy gap between the individual bonding MOs will be negligible for all intents and purposes. These orbitals produce what is essentially a continuous band of (low-energy) bonding MOs and a continuous band of (higher-energy) anti-bonding MOs. The energy gap between the bonding and anti-bonding orbitals is called the band-gap and in a metal this band-gap is quite small (recall that the gap between the bonding and anti-bonding MOs in diamond is very large). Moreover in metals the bonding MOs (known as the valence band) are able to accommodate more electrons. This is because in metals there are typically fewer electrons than there are atomic orbitals. Consider aluminum: it has three valence electrons and in the ground (lowest energy) state has an electron configuration of 3s2 3p1. This suggests that it has two unoccupied 3p orbitals. We can consider the bonding MOs in aluminum to be formed from all the available atomic orbitals, which means that there are many bonding MOs that are not occupied by electrons. The physical consequences of this are that the valence electrons can move relatively easily from one MO to another because their energies are very close together. Whereas nuclei and core electrons remain more or less locked in position the valence electrons can spread out to form a kind of electron sea within the metal. When an electrical potential is applied across the metal, electrons from an external source can easily enter the valence band and electrons can just as easily leave the metal. Electrical conductivity is essentially a measure of how easily electrons can flow through a substance. Metals typically have high conductivity due to the ease with which electrons can move from one MO to another and the fact that each MO extends throughout the whole piece of metal. Because the numbers of electrons entering and leaving are the same, the piece of metal remains uncharged.
In this model the atomic cores are packed together and surrounded by a cloud of electrons that serve as the “glue” that binds them together. There are no discrete bonds in this type of structure. When a piece of metal is put under physical stress (for example it is stretched or deformed) the atoms can move relative to one another but the electrons remain spread throughout the structure. Metals can often be slowly deformed into different shapes without losing their structural integrity or electrical conductivity—they are malleable! They can be melted (increased atomic movement), become liquid, and then allowed to cool until they solidify; throughout this process they retain their integrity and their metallic properties and so continue to conduct electricity.[17] This is quite different from how other substances (such as diamond or water) behave. The hardness of a solid metal depends on how well its atoms packed together and how many electrons are contributed to the valence band of orbitals.
So why do some elements behave as metals and others do not? For example graphite conducts electricity but it is not malleable and can’t be heated and molded into other shapes. The answer lies in the behavior of the MOs and the resulting bonds they can produce. Graphite has a rigid backbone of carbon–carbon bonds that makes it strong and stable but overlaying those bonds is the set of delocalized MOs that spread out over the whole sheet. As a result graphite has some properties that are similar to diamond (stability and strength), some that are similar to metals (electrical conductivity), and some that are a consequence of its unique sheet structure (slipperiness).
Why Are Metals Shiny?
We see things because photons hit the back of our retinas and are absorbed by specialized molecules (proteins and associated pigment molecules). This leads to changes in protein structure and initiates a cascade of neuron-based cellular events that alters brain activity. So where do these photons come from? First and foremost they can be emitted from a source (the Sun, a light bulb, etc.) that appears to shine and can be seen in the dark. Alternatively, photons can be reflected off a surface; in fact most of the things we see do not emit light, but rather reflect it. A red T-shirt appears red because it absorbs other colors and reflects red light. Photons can also be refracted when they pass through a substance. A cut diamond sparkles because light is refracted as it passes through the material and exits from the many facets. Refraction is caused when photons bump into electrons, are absorbed, and then (very shortly thereafter) are re-emitted as they travel through a material. These processes take time, so the apparent speed of light slows down. It can take a photon many thousands of years to move from the core to the surface of the Sun because of all the collisions that it makes during the journey.[18]
To explain why metals (and graphite) are shiny, we invoke a combination of reflection, refraction, and the energy levels of MOs. When a photon of light is absorbed and reemitted, the electron moves from one orbital to another. Let us consider a piece of metal at room temperature. When a photon arrives at the metal’s surface it encounters the almost continuous band of MOs. Most photons, regardless of their wavelength, can be absorbed because there is an energy gap between orbitals corresponding to the energy of the photon. This process promotes electrons up to a higher energy level. As the electrons drop back down to a lower energy level, the photons are re-emitted, resulting in the characteristic metallic luster. Metals actually emit light, although this does not mean metals glow in the dark (like a light bulb or the Sun). Instead, metals absorb and re-emit photons, even at room temperature.
The color of a particular metal depends upon the range of wavelengths that are re-emitted. For most metals the photons re-emitted have a wide range of wavelengths which makes the metallic surface silvery. A few metals, such as copper and gold, absorb light in the blue region and re-emit light with wavelengths that are biased toward the red end region of the spectrum (400–700 nm) and therefore they appear yellowish. This is due to relativistic effects way beyond the scope of this book, but something to look forward to in your future physical chemistry studies!
Now we can also understand why metals emit light when they are heated. The kinetic energy of the atoms increases with temperature which promotes electrons from low to higher energy orbitals. When these electrons lose that energy by returning to the ground state, it is emitted as light. The higher the temperature the shorter the wavelength of the emitted light. As a filament heats up, it first glows red and then increasing whiter as photons of more and more wavelengths are emitted.
Questions
Questions to Answer
- What properties indicate that a substance is metallic?
- Why are metals shiny?
- How can metallic properties be explained by the atomic-molecular structure of Al (for example)?
- Why can we see through diamond but not aluminum? How about graphite?
- Why does aluminum (and for that matter all metals) conduct electricity? What must be happening at the atomic-molecular scale for this to occur?
- What does the fact that diamond doesn’t conduct electricity tell you about the bonding in diamond?
- How do the bonding models for diamond and graphite explain the differences in properties between diamond, graphite, and a metal like aluminum?
- Why is it OK to use different models to describe bonding in different species?
This chapter has brought us to a point where we should have a fairly good idea of the kinds of interactions that can occur among atoms of the same element. We have seen that the properties of different elements can be explained by considering the structure of their atoms and in particular the way their electrons behave as the atoms interact to form molecules or large assemblies of atoms (like diamond.) What we have not considered yet is how atoms of different elements interact to form compounds (substances that have more than one element). In Chapter 4 we will take up this subject and much more.
- http://www.space.com/scienceastronomy/mystery_monday_040524.html ↵
- http://www.youtube.com/watch?v=th_9ZR2I0_w&feature=c4-overview&list=UUUHW94eEFW7hkUMVaZz4eDg ↵
- http://www.astro.ucla.edu/~wright/BBhistory.html ↵
- In this nomenclature (described more on the web), the first superscript number is the number of proton and neutrons, while the second superscript number is the number of protons; both numbers are always integers. The letter is the symbol of the element, e.g. He for helium or Li for lithium. ↵
- Nuclear fusion releases huge amounts of energy (some of the mass is transformed into energy). On Earth, controllable nuclear fusion has long been a potential target in the search for new energy sources, but so far the energy required to bring about the initial fusion has not been replaced when the fusion occurs – i.e., nuclear fusion reactors have yet to break even. Uncontrolled nuclear fusion takes place in hydrogen bombs – clearly not a viable option for a useful energy source at the moment. Nuclear fusion does however take place in stars, and is self-sustaining. The reason you can see and feel the energy from the Sun is that is it undergoing nuclear fusion reactions, which supply us with almost all the energy that is used on Earth today. ↵
- It has been estimated that it takes between 10,000 to 170,000 years for a photon released during a fusion reaction at the Sun’s core to reach its surface. http://sunearthday.nasa.gov/2007/locations/ttt_sunlight.php ↵
- More physics that we will conveniently pass over, but it is worth noting that this is why the planets all move around the Sun in the same direction. ↵
- You may want to search the web for “extrasolar planets.” ↵
- For those who want more, rest assured that you will find out if you take more advanced classes either in physics or physical chemistry. ↵
- This study shows images of bonds forming http://www.sciencemag.org/content/340/6139/1434.abstract ↵
- Although perhaps the word orbital is confusing because it implies a circular or elliptical motion, what we mean is the volume in which there is a 90% probability of finding an electron. That said, orbitals are the way chemists (and the occasional physicist) talk, so we have to use it. ↵
- How much pressure is that exactly in real world terms? ↵
- http://en.wikipedia.org/wiki/X-ray_crystallography ↵
- In fact the sheets in graphite do not slip relative to each other very readily. On Earth graphite is a lubricant, but in space in the absence of small molecules like O2, N2 and H2O, graphite does not lubricate. It is thought that the sheets slip relative to each other as if they were rolling on ball bearings (the small molecules). As you might imagine, this discovery caused some consternation in high-flying airplanes where the engines began to fail because of lack of lubrication. ↵
- The Nobel Prize in Physics was awarded in 2010 for the discovery of graphene. http://nobelprize.org/nobel_prizes/physics/laureates/2010/ ↵
- In 1996 Smalley, Kroto, and Curl were awarded the Nobel Prize in Chemistry for the discovery of fullerenes. http://nobelprize.org/nobel_prizes/chemistry/laureates/1996/ ↵
- We need to mentions (at least) what electricity is, i.e. the flow of electrons. ↵
- Robert Naeye (1998). Through the Eyes of Hubble: Birth, Life and Violent Death of Stars. CRC Press. ISBN 0750304847. Of course this raises the question, is it the same photon? ↵

