5 Systems Thinking
Melanie M. Cooper and Michael W. Klymkowsky

Let us recap where we are with atoms, at least from a chemistry perspective:
- Atoms interact electrostatically with each other in a variety of ways, from transient interactions that result in weak (easy to overcome) attractions to strong (bonding) interactions that are much more difficult to break.
- When atoms interact they form more stable systems, where the attractive and repulsive interactions are equal. The potential energy of the system decreases but the total energy of the system remains constant. The total energy of the interacting atoms (the system) can decrease if it is transferred to the surroundings, usually by collisions with other molecules or atoms but the emission of a photon is also possible.
- Whether weak or strong, all types of interactions require energy to overcome. Typically this energy is derived from collisions with surrounding molecules, although absorption of a photon can also overcome interactions.
- The ways that atoms interact depend upon the arrangements of the electrons within them. Different types of atoms have different “internal” arrangements of electrons.
- When atoms bond to form new materials (compounds), the properties of those compounds are emergent—that is, they are quite different from the properties of the isolated component atoms.
- The macroscopic properties of materials depend upon the types of bonds present and their spatial organization, which influences molecular shape, the distribution of charges within the molecule, and intermolecular interactions.
- Some materials are continuous (diamond, metals, ionic compounds), whereas others are composed of discrete molecular units (water, methane, lipids, proteins).
- If you know the temperature at which phase changes occur in a material (solid to liquid, liquid to gas, etc.), you can make predictions about how much energy is required to overcome the interactions between the particles that make up the material.
Now we are ready to draw all these ideas together and make connections between the macroscopic and molecular levels. Understanding these connections allows us to predict how and when chemical changes will occur, which is the heart of chemistry.
5.1 Temperature
Up to now the major types of change we have considered are phase changes (solid to liquid, liquid to gas, etc.) Now we will look at the elements of a phase change in greater detail starting with temperature. If you look up the definition of temperature you will probably find something like “the degree of heat of an object” and think to yourself, “Well, that’s not very illuminating, is it?” However, it is actually quite difficult to give a simple definition of temperature, (typically abbreviated as T). If you were already taught about temperature in physics courses, please bear with us (a chemist and a cell and molecular biologist) as we work our way through it, sometimes it it helpful to think about things you already know in new ways!
A useful macroscopic way of thinking about temperature is that it tells you in which direction thermal energy (often called heat) will move—energy always moves from a hotter (higher-temperature) object to a cooler (lower-temperature) one. This may seem like an obvious statement about how the physical world works but do you really know why it must be the case? Why doesn’t heat flow from cooler to warmer? Is there some principle that will allow us to to explain why? We will be coming back to these questions later on in this chapter.
Students often confuse temperature and thermal energy and before we go on we need to have a good grasp of the difference between them. The temperature of an object is independent of the size of the object, at least until we get down to the atomic/molecular level where temperature begins to lose its meaning as a concept.[1] The temperature of a drop of boiling water is the same as the temperature of a pan (or an ocean) of boiling water: 100 °C at sea level. At the same time the total amount of thermal energy in a drop of water is much less than that in a large pot of water at the same temperature. A drop of boiling water may sting for a moment if it lands on you, but a pan of boiling water will cause serious damage if it splashes over you. Why? Even though the two are at the same temperature, one has relatively little thermal energy and the other has a lot; the amount of energy is related to the size of the system. In addition, the amount of thermal energy depends on the type, that is, the composition of the material. Different amounts of different substances can have different amounts of thermal energy, even if they are at the same temperature (weird but true).
Kinetic Energy and Temperature
Another way of thinking about temperature is that it is related to the energy of the particles in the sample: the faster the particles are moving, the higher the temperature. It may well take different amounts of energy to get particles moving at the same average kinetic energy. For a simple monoatomic gas, like helium or neon, the only motion that the atoms can do is to move from one place to another in a straight line until they bump into something else, such as another atom or molecule.[2] This kind of motion is called translational motion and is directly linked to the kinetic energy of the atom or molecule through the relationship KE = 1/2 m v(bar) 2 = 3/2 kT where v(bar) is the average velocity of all of the molecules in the population[3], m is the mass, k is a constant, known as the Boltzmann constant, and T is the temperature. That is, the average kinetic energy of a gas is directly related to the temperature. In any given gaseous sample of moving atoms there are many collisions per unit time but these collisions do not alter the total energy of the system (it is conserved).[4] What these collision can, and often do, alter is the relative kinetic energies of the two (or more) colliding atoms: if one slows down, the other will speed up (remember, we are now talking only about monoatomic species; things get more complicated with more complex molecules).
Any single atom or molecule has kinetic energy, but not a temperature. This is an important distinction. Populations of molecules have a temperature related to their average velocity but the concept of temperature is not relevant to individual molecules, they have kinetic energy but not a temperature. This is a important idea, temperature as a characteristic of a system not its individual components. While a system has a unique temperature, the individual molecules that make up the system can have quite different kinetic energies. Because of collisions between molecules, an individual molecule’s kinetic energy can be changing rapidly, even though the temperature of the system is constant. When it comes to chemical reactions, it is individual kinetic energies that will be critical (we consider this point in greater detail in Chapter 7).
5.2 Thinking About Populations of Molecules
Within a population of atoms and molecules, the many collisions that occur per second lead to a range of speeds and directions (that is, velocities) of the atoms/molecules. When large numbers of particles are involved in a phenomenon, their individual actions are not important, for example when measuring temperature or pressure (although they are when individual molecules collide, that is, take part in chemical reactions). We treat large numbers of molecules as a population. A population is characterized by the distribution of the number or probability of molecules moving with various velocities.[5] This makes it possible to use statistical methods to characterize the behavior of the population. Although any particular molecule behaves differently from one moment to the next, depending upon whether it collides with other molecules or not, the behavior of the population is quite predictable.[6]
From this population perspective, it is the distribution of kinetic energies of atoms or molecules that depends upon the temperature of the system. We will not concern ourselves with deriving the equations that describe these relationships, but rather focus on a general description of the behavior of the motions of atoms and molecules in various states of matter.
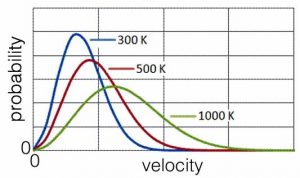
Let us think about a population of molecules at a particular temperature in the gas phase. Because of their constant collisions with one another, the population of molecules has a distribution of speeds. We can calculate the probability of a particular molecule moving at a particular speed. This relationship is known as the Maxwell–Boltzmann distribution, shown in the graph. Its shape is a function of the temperature of the system; typically it rises fairly steeply from zero (all of the curves begin at zero – why is that do you think?) to a maximum, which then decreases and tails off at higher velocities (which correspond to higher kinetic energies). Because we are plotting probability versus kinetic energy (or rms velocity or speed) we can set the area under the curve to be equal to one (or any other constant). As the temperature changes, the area under the curve stays constant. Why? Because we are completely certain that each particle has some defined amount of kinetic energy (or velocity or speed), even if it is zero and even if we could not possibly know it (remember the uncertainty principle). As the temperature is increased, the relative number of particles that are moving at higher speeds and with more kinetic energy increases. The shape of the curve flattens out and becomes broader. There are still molecules moving very slowly, but there are relatively fewer of them. The most probable speed (the peak of the curve) and the average speed (which is a little higher since the curve is not symmetrical) increase as the temperature increases.
Questions
Questions to Answer
- What happens to the average speed of molecules as temperature increases?
- When molecules collide, why don’t they stick together?
- What do you think happens to the average speed as molecular weight increases (assuming the temperature stays the same)?
- Imagine a system composed of two different types of molecules, one much heavier than the other. At a particular temperature, how do their average kinetic energies compare? Which, on average, is moving faster?
Questions to Ponder
- How large does a system have to be to have a temperature, 10 molecules or 10,000,000?
- If one considers the uncertainty principle, what is the slowest velocity at which a molecule can move?
- If you place a thermometer into a solution, why does it take time for the reading on the thermometer to correspond to the temperature of the solution?
Temperature, Kinetic Energy and Gases
Now here is an unexpected fact: the average kinetic energies of molecules of any gas at the same temperature are equal (since KE = 3/2kT, the identity of the gas does not matter). Let us think about how that could be true and what it implies about gases. Under most circumstances the molecules in a gas do not significantly interact with each other; all they do is collide with one another like billiard balls. So when two gases are at the same temperature, their molecules have the same average kinetic energy. However, an even more unexpected fact is that the mass of the molecules of one gas is different from the mass of the molecules of the other gas. Therefore, given that the average kinetic energies are the same, but the molecular masses are different, the average velocities of molecules in the two gases must be different. For example, let us compare molecular hydrogen (H2 ) gas (molecular weight = 2 g/mol) with molecular oxygen (O2) gas (molecular weight = 32 g/mol), at the same temperature. Since they are at the same temperature the average kinetic energy of H2 must be equal to the average kinetic energy of O2, then the H2 molecules must be moving, on average, faster than the O2 molecules.[7]
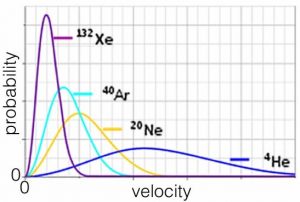
So the average speed at which an atom or molecule moves depends on its mass. Heavier particles move more slowly, on average, which makes perfect sense. Consider a plot of the behavior of the noble (monoatomic) gases, all at the same temperature. On average helium atoms move much faster than xenon atoms, which are over 30 times heavier. As a side note, gas molecules tend to move very fast. At 0 °C the average H2 molecule is moving at about 2000 m/s, which is more than a mile per second and the average O2 molecule is moving at approximately 500 m/s. This explains why smells travel relatively fast: if someone spills perfume on one side of a room, you can smell it almost instantaneously. It also explains why you can’t smell something unless it is a gas. We will return to this idea later.
Questions
Questions to Answer
- Why don’t all gas particles move with the same speed at a given temperature?
- Where would krypton appear on the plot above? Why?
- Consider air, a gas composed primarily of N2, O2, and CO2. At a particular temperature, how do the average kinetic energies of these molecules compare to one another?
- What would a plot of kinetic energy versus probability look like for the same gas at different temperatures?
- What would a plot of kinetic energy (rather than speed) versus probability look like for different gases (e.g., the noble gases) at the same temperature?
Questions to Ponder
- If gas molecules are moving so fast (around 500 m/s), why do most smells travel at significantly less than that?
- Why does it not matter much if we use speed, velocity, or kinetic energy to present the distribution of motion of particles in a system (assuming the particles are all the same)?
5.3 Vibrating, Bending, and Rotating Molecules
As we have already seen the average kinetic energy of a gas sample can be directly related to temperature by the equation Ek(bar) = 1/2 mv(bar)2 = 3/2 kT where v(bar) is the average velocity and k is a constant, known as the Boltzmann constant. So, you might reasonably conclude that when the temperature is 0 K, all movement stops. However, if a molecule stops moving we should be able to tell exactly where it is, right? Oh no! That would violate the uncertainty principle, which means there will need be some uncertainty in its energy! At 0 K (a temperature that cannot be reached, even in theory) the system will have what is called zero point energy: the energy that remains when all the other energy is removed from a system (a quantum mechanical concept completely irrelevant to normal life).
For monoatomic gases, temperature is a measure of the average kinetic energy of molecules. But for systems made up of more complex molecules composed of multiple atoms, there are other ways to store energy besides translation (that is, moving through space). In these situations energy added to a system can not only speed up the movement of molecules but also make them vibrate, bend, and rotate (recall we discussed this briefly in Chapter 4)(FIG→). These vibrations, bends, and rotations are distinct for each type of molecule; they depend upon molecular shape and composition. Perhaps not surprisingly, they are quantized. This means that only certain packets of energy can be absorbed or released depending on which vibrations or rotations are involved.[8] Because of that, we can use these molecule-specific energy states to identify molecules and determine their structure at the atomic level. Just as we can identify atoms of elements by their electronic spectra (how their electrons absorb and emit photons as they move from one quantum level to another), we can identify molecules by the way they absorb or emit photons as the molecule moves from one vibrational or rotational state to another. Because it takes less energy to move between vibrational states, photons of infrared or microwave frequencies are typically involved in this analysis. This is the basis for infrared spectroscopy, a topic that we will return to in a separate work.
As materials become more complex in structure, more energy is needed to increase their temperature because there are more ways for a complex molecule to vibrate, bend, and rotate; some of the added energy is used up in vibrations and rotations as well as translations. The amount of energy required to raise the temperature of a particular amount of substance is determined by the molecular-level structure of the material. We can do experiments to determine how adding energy to a substance affects its temperature. Although the word heat is sometimes used to describe thermal energy, in the world of physics it is specifically used to describe the transfer of thermal energy from one thing to another. So, we will stick with thermal energy here.
The units of thermal energy are joules (J).[9] Thermal energy is the sum of the kinetic and other potential energies of the particles in a system. There are two commonly used measures of how much energy it takes to change the temperature of a substance and, conversely, how much energy a substance can store at a given temperature: specific heat capacity (J/g ºC) and molar heat capacity (J/mol ºC). The specific heat of a substance tells you how much energy is required to raise the temperature of a mass (1 g) of material by 1 ºC; the molar heat capacity tells you how much energy is required to raise the temperature of a mole of particles by 1 ºC. The specific heats and molar heat capacity of a substance depend on both the molecular structure and intermolecular interactions (for solids and liquids, but not gases). Usually, more complex substances have a higher molar heat capacity because larger molecules have more possible ways to vibrate, bend, and rotate. Substances with strong IMFs tend to have higher heat capacities than those with weaker IMFs because energy must be used to overcome the interactions between molecules, rather than make the substance move faster – which increases the temperature.
Heat Capacity and Molecular Structure
It takes 4.12 J to raise 1 gram of water 1 ºC (or 1 K.) If you add energy to a pan of water by heating it on a stove top energy is transferred to the molecules of water by collisions with the pan, which in turn has heated up from contact with the heating element[10]. The addition of energy to the system results in the faster movement of molecules, which includes moving from place to place, rotating, bending, and vibrating. Each type of movement adds to the overall thermal energy of the material. Although the molecules in a gas very rarely interact with one another, those in a solid and liquid interact constantly. The increase in temperature as a function of added energy is relatively simple to calculate for a gas; it is much more complicated for liquids and solids, where it depends upon molecular structure and intramolecular (within a molecule) as well as intermolecular (between molecules) interactions.
Consider the molar heat capacities and specific heats of water and the hydrocarbon alcohols (which contain an -OH group) methanol, ethanol, and propanol. As you can see in the table below, water has an unusually high specific heat, even though it is smaller than the other molecules. Their specific heats are pretty much constant, but their molar heat capacities increase with molar mass.
| Name | Formula | Molar Mass, g | Molar Heat Capacity
J/mol ºC |
Specific Heat
J/g ºC |
| Water | H2O | 18 | 75.4 | 4.18 |
| Methanol | CH3OH | 32 | 81.0 | 2.53 |
| Ethanol | CH3CH2OH | 48 | 112 | 2.44 |
| Propanol | CH3CH2CH2OH | 60 | 144 | 2.39 |
So an obvious question is, why is the specific heat of water so much higher than that of these alcohols? The reasons for this (apparent) anomaly are:
- Water molecules are smaller so there are more molecules per gram than there are in the larger, more complex substances.
- Each water molecule can form up to four hydrogen bonds, but the alcohols can only form a maximum of two hydrogen bonds each (why is this?). As thermal energy is added to the system some of that energy must be used to overcome the attractive forces between molecules (that is, hydrogen bonds) before it can be used to increase the average speed of the molecules. Because there are more hydrogen bonds forming attractions between water molecules, it takes more energy to overcome those interactions and raise the kinetic energy of the water molecules. The end result is a smaller increase in temperature for the same amount of energy added to water compared to methanol, ethanol, and propanol.
The relatively high specific heat of water has important ramifications for us. About 70% of the Earth’s surface is covered with water. Because of water’s high specific heat, changes in the amounts of solar energy falling on an area between day and night are “evened out” by the large amount of water in the oceans. During the day, the water absorbs much of the energy radiated from the sun, but without a drastic temperature increase. At night, as the temperature falls, the oceans release some of this stored energy, thus keeping the temperature fluctuations relatively small. This effect moderates what would otherwise be dramatic daily changes in surface temperature. In contrast, surface temperatures of waterless areas (like deserts), planets (like Mars), and the Moon fluctuate much more dramatically, because there is no water to absorb and release thermal energy.[11] This moderation of day–night temperature change is likely to be one of the factors that made it possible for life to originate, survive, and evolve on the early Earth. As we go on, we will see other aspects of water’s behavior that are critical to life.
Removing Thermal Energy from a Gas
Now that we have been formally introduced to the concepts of heat, thermal energy, and temperature, we can examine what happens when energy is added or removed from matter. We begin with a gas because it is the simplest form of matter. We can observe a gas system by looking at a sealed container of water vapor. We can reduce the temperature by cooling the walls of the container; as gas molecules collide with the walls, some of their energy is transferred to the wall and then removed by the cooling system. Over time, the average kinetic energy of the molecules (temperature) decreases. We know that all molecules are attracted to one another by London dispersion forces. In the case of water molecules, there are also interactions mediated by the ability to make hydrogen bonds and dipole–dipole interactions. As temperature increases, these relatively weak interactions are not strong enough to keep molecules stuck together; they are broken during molecular collisions. As the temperature drops, and the average kinetic energy decreases, more and more of these interactions persist for longer and longer times. This enables groups of molecules to form increasingly larger and heavier aggregates. Assuming that our container is on the surface of the Earth, molecules fall out or condense out of the gaseous phase to form a liquid. Because the molecules in the liquid are interacting closely with one another, the volume occupied by these aggregates is much smaller than the volume occupied by the same number of molecules in a gas. The density (mass/volume) of the liquid is higher, and eventually these drops of liquid become large enough to feel the effect of gravity, and are attracted towards the Earth. As the drops of liquid fall to the bottom of the container they merge with one another and the liquid phase below separates from the gaseous phase above. The temperature where the liquid phase first appears is the boiling (or condensation) point of the material (for water it is 100 ºC under atmospheric pressure at sea level). If we continue to remove energy from the system at a fairly slow, steady rate, the temperature will not change until almost all the water vapor has condensed into liquid. Why do you think this is so? It may be easier to think about the reverse process: when water boils, the temperature of the water does not change until almost all the water in the liquid phase has vaporized, even though energy is being added to the system. What is that energy being used for?
Even at temperatures well below the boiling point there are still some molecules in the gaseous phase. Why? Because within the liquid, some molecules are moving fast enough (and are located close enough to the liquid–gas boundary) to break the interactions holding them in the liquid. When they leave the liquid phase, the average kinetic energy of the liquid drops (the molecules that leave have higher than average kinetic energy) and some of the kinetic energy of the escaping molecules is used to break free of the interactions holding them together in the liquid phase. The escaping molecules now have lower kinetic energy. This is the basis of the process known as evaporative cooling. The same process explains how the evaporation of sweat cools your body.
Questions
Questions to Answer
- Can you measure thermal energy directly? Why or why not?
- What can we measure changes in? How does that allow us to figure out changes in thermal energy of a system?
- Draw a graph of the change in temperature when equal amounts of thermal energy are added at the same rate to equal masses of water, ethanol, and propanol.
- Does each sample reach the same temperature? Why or why not?
- Plot the temperature change versus time as a sample of water vapor moves from a temperature of 110 ºC to 90 ºC.
- Draw a molecular-level picture of what the sample looks like at 110 ºC and 90 ºC. Explain what is happening in each different part of your graph.
- When energy is added to and the water boils, the temperature stays at 100 ºC until almost all the water is gone. What is the energy being used for?
Questions to Ponder
- What would life be like if we lived on a planet with no water, but instead the oceans were filled with methanol or ammonia (or filled with hydrocarbons as on Titan, a moon of Saturn)?
- After it’s just finished raining, why do pools of water disappear even when the temperature is below the boiling point of water?
- Clouds are made from small droplets of water, why don’t they fall to Earth?
Liquids to Solids and Back Again
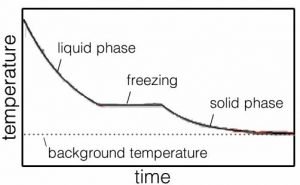
Within a liquid, molecules move with respect to one another. That is why liquids flow. What does that mean at the molecular level? It means that the molecules are (on average) moving fast enough to break some, but not all, of the interactions linking them to their neighbors. But let us consider what happens as we remove more and more energy from the system through interactions of the molecules with the container’s walls. With less energy in the system, there is a decrease in the frequency with which molecules have sufficient energy to break the interactions between them, and as a result interactions become more stable. Once most interactions are stable the substance becomes a solid. The temperature at which the material goes from solid to liquid is termed the melting point. A liquid becomes a solid at the freezing point. For water at atmospheric pressure, this is 0 ºC (or 273.15 K). Just like the boiling/condensation point, the temperature does not change appreciably until all the liquid has solidified into ice, or all the ice has melted (→).
Molecular shape and the geometry of the interactions between molecules determine what happens when water (or any other liquid) is cooled and eventually freezes. In the case of frozen water (ice) there are more than 15 types of arrangements of the molecules, ranging from amorphous to various types of crystalline ice. In amorphous ice, the molecules occupy positions that are more or less random with respect to their neighbors; in contrast the molecules in crystalline ice have very specific orientations to one another. The form of ice we are most familiar with is known as Ice Ih, in which the water molecules are organized in a hexagonal, three-dimensional array. Each molecule is linked to four neighboring molecules through hydrogen bonds. This molecular-level structure is reflected at the macroscopic level, which is why snowflakes are hexagonal. Once frozen, the molecules can no longer move with respect to one another because of the bonds between them; the ice is solid and retains it shape, at both the visible and the invisible (molecular) level. However, because we are not at absolute zero (0 K or -273.15 ºC), the molecules are still vibrating in place.
Now, what would happen if we heated our container transferring energy from the surroundings into the system (the ice)? As energy is added to the ice the water molecules vibrate more and more vigorously and eventually the hydrogen bonding interactions holding the molecules in place are overcome and the molecules become free to move relative to one another other. The ice melts. At this temperature (0 ºC, 273.15 K) all the energy entering the system is used to overcome intermolecular attractions, rather than increase the speed of molecular motion. If the system is well mixed, the temperature stays at 0 ºC until all of the ice has melted. Then the temperature starts to rise again as the water molecules, now free to move relative to each other, increase in kinetic energy.
Because of the arrangement of water molecules in Ice Ih, the hexagonal “cages” of water molecules within the crystal have empty space within them. As the hydrogen bonds break, some of the water molecules can now move closer together to fill in these open spaces. The structure of the ice collapses in on itself. This open network of molecules, which is not present in liquid water, means that Ice Ih is less dense than liquid water, which is why it floats on liquid water. We don’t think much of this commonplace observation, but it is quite rare for a solid to be less dense than the corresponding liquid. More typically, materials (particularly gases, but also liquids and solids) expand when heated as a consequence of the increased kinetic energy, making the particles vibrate more vigorously and take up more space.
5.4 Open Versus Closed Systems
In our discussion, the container of water vapor (gas) is our system: the part of the universe we are observing. It is separated from the rest of the universe (its surroundings) by the walls of the container (its boundary).[12] When we remove energy from the system or add energy to it, that energy goes to or comes from the surroundings. Our system is not an isolated system. If it were, neither energy nor matter would move between the system and the surroundings. In practice it is difficult to construct a perfectly isolated system (although an insulated or styrofoam coffee cup with a lid on is not a bad approximation.) We can also distinguish between open and closed systems: in an open system both matter and energy can enter or leave (we can keep track of both) whereas in a closed system the amount of matter is constant and only energy can enter or leave. Whenever we look at a system our first task is to decide whether the system is isolated, open, or closed. All biological systems are open (both energy and matter are being exchanged with the surroundings.) In the absence of such an exchange, a biological system would eventually die.[13]
Let us consider a beaker of water without a lid as our open system. As the temperature rises, some of the water molecules have enough energy to escape from the body of the water. The liquid water evaporates (changes to a gas). Any gases that might be dissolved in the liquid water, such as oxygen (O2) or nitrogen (N2), also move from the liquid to the gaseous phase. At the boiling point, all the energy being supplied to the system is being used to overcome the intermolecular forces, as it was at the melting point. However, this time the molecules are completely separated from one another, although they still collide periodically. Thus energy is used to overcome attractive forces and the individual molecules fly off into the gas phase where the distances between them become so great that the attractive forces are insignificant.[14] As the liquid boils, its temperature does not rise until all of it has been transformed from liquid to vapor. As the gas molecules fly off, they carry with them some of the system’s energy.
Questions
Questions to Answer
- Begin with an ice cube in a beaker and end with water vapor. Draw a graph of the energy input versus the temperature of the system. Is your graph a straight line?
- What would happen to the mass of the beaker and water during this process?
- Can you reproduce the hexagonal symmetry of ice by using a model kit? What property of hydrogen bonds makes the structure so open?
- As the temperature rises in liquid water, what do you think happens to the density? Draw a plot of density versus temperature for a mass of water beginning at -10 ºC, up to 50 ºC.
- What happens when the temperature has risen such that the molecules have enough energy to overcome all the attractions between the separate molecules? Focus not on the covalent bonds but the attractions between separate molecules.
Questions to Answer, continued
- During evaporation and boiling do water molecules ever return to the liquid?
- Estimate the temperature at which the bonds within a water molecule break. How does that temperature compare to the boiling point of water? Why aren’t they the same temperature?
- How would an open and a closed system differ if you heated them from 30 to 110ºC?
Questions to Ponder
- Are boiling and evaporation fundamentally different processes?
- Under what conditions does evaporation not occur? What is happening at the molecular level?
- What is in the spaces in the middle of the hexagonal holes in Ice Ih?
- What would be the consequences for a closed or isolated biological system?
Questions for Later
- As you heat up a solution of water, predict whether water molecules or dissolved gas molecules will preferentially move from the liquid to the gaseous phase (or will they all move at the same rate?). What factors do you think are responsible for “holding” the gas molecules in the water?
- What do you think happens to the density of the gas (in a closed system) as you increase the temperature?
- What would happen if you captured the gas in a container?
- What would happen if you took that gas in the container and compressed it (made the volume of the container much smaller)?
5.5 Thermodynamics and Systems
The study of how energy in its various forms moves through a system is called thermodynamics. In chemistry specifically it is called thermochemistry. The first law of thermodynamics tells us that energy can be neither created nor destroyed but it can be transferred from a system to its surroundings and vice versa.[15] For any system, if we add up the kinetic and potential energies of all of the particles that make up the substance we get the total energy. This is called the system’s internal energy, abbreviated as E in chemistry.[16] It turns out that it is not really possible to measure the total internal energy of a system. But we can measure and calculate the change in internal energy represented as ΔE (we use the Greek letter Δ to stand for change). There are two ways that the internal energy of a system can change: we can change the total amount of thermal energy in the system (denoted as q), or the system can do work or have work done to it (denoted as w). The change in internal energy is therefore:
ΔE = q + w
At the molecular level, it should now be relatively easy to imagine the effects of adding or removing thermal energy from a system. However work (usually defined as force multiplied by distance) done on or by the system is a macroscopic phenomenon. If the system comes to occupy a larger or smaller volume, work must be done on the surroundings or on the system, respectively. With the exception of gases, most systems we study in chemistry do not expand or contract significantly. In these situations, ΔE = q, the change in thermal energy (heat). In addition, most of the systems we study in chemistry and biology are under constant pressure (usually atmospheric pressure). Heat change at constant pressure is what is known as a state function, it is called enthalpy (H). A state function is a property of a system that does not depend upon the path taken to get to a particular state. Typically we use upper case symbols (for example, H, T, P, E, G, S) to signify state functions, and lower case symbols for properties that depend on the path by which the change is made (for example, q and w). You may be wondering what the difference between a state and path function is. Imagine you are climbing Mount Everest. If you were able to fly in a balloon from the base camp to the top you would travel a certain distance and the height change would be 29,029 feet. Now in contrast if you traveled on foot, via any one of the recorded paths – which wind around the mountain you would travel very different distances – but the height change would still be 29,029 feet. That is the distance travelled is a path function and the height of Mt Everest is a state function. Similarly, both q and ΔH describe thermal energy changes but q depends on the path and ΔH does not. In a system at constant pressure with no volume change, it is the change in enthalpy (ΔH) that we will be primarily interested in (together with the change in entropy (ΔS), which we examine shortly in greater detail).
Because we cannot measure energy changes directly we have to use some observable (and measurable) change in the system. Typically we measure the temperature change and then relate it to the energy change. For changes that occur at constant pressure and volume this energy change is the enthalpy change, ΔH. If we know the temperature change (ΔT), the amount (mass) of material and its specific heat, we can calculate the enthalpy change:
ΔH (J) = mass (g) x specific heat (J/g ºC) x ΔT (ºC).[17]
When considering the enthalpy change for a process, the direction of energy transfer is important. By convention, if thermal energy goes out of the system to the surroundings (that is, the surroundings increase in temperature), the sign of ΔH is negative and we say the process is exothermic (literally, “heat out”). Combustion reactions, such as burning wood or gasoline in air, are probably the most common examples of exothermic processes. In contrast, if a process requires thermal energy from the surroundings to make it happen, the sign of ΔH is positive and we say the process is endothermic (energy is transferred from the surroundings to the system).
Questions
Questions to Answer
- You have systems (at 10 ºC) composed of water, methanol, ethanol, or propanol. Predict the final temperature of each system if equal amounts of thermal energy (q) are added to equal amounts of a substance (m). What do you need to know to do this calculation?
- Draw a simple sketch of a system and surroundings. Indicate by the use of arrows what we mean by an endothermic process and an exothermic process. What is the sign of ΔH for each process?
- Draw a similar diagram and show the direction and sign of work (w) when the system does work on the surroundings (expands), and when the surroundings do work on the system (contracts).
- Draw a diagram to show the molecular level mechanism by which thermal energy is transferred in or out of a system. For example how is thermal energy transferred as an ice cube melts in a glass of water?
Questions to Ponder
- What does the difference in behavior of water, methanol, ethanol, and propane tell us about their molecular behavior/organization/structure?
The Second Law of Thermodynamics
Whereas the first law of thermodynamics states that you cannot get more energy out of a system than is already present in some form, the second law of thermodynamics tells us that we cannot even get back the energy that we use to bring about a change in a system. The idea in the second law is captured by the phrase “for any change in a system, the total entropy of the universe must increase.” As we will see, this means that some of the energy is changed into a form that is no longer useful (that is, it cannot do work).
There are lots of subtle and not so subtle implications captured by this statement and we will need to look at them carefully to identify them. You may already have some idea of what entropy means, but can you define it? As you might imagine it is not a simple idea. The word entropy is often used to designate randomness or disorder but this is not a very useful or accurate way to define entropy (although randomly disordered systems do have high entropy). A better way to think about entropy is in terms of probabilities: how to measure, calculate, and predict outcomes. Thermal energy transfers from hot to cold systems because the outcome is the most probable outcome. A drop of dye disperses in water because the resulting dispersed distribution of dye molecules is the most probable. Osmosis occurs when water passes through a membrane from a dilute to a more concentrated solution because the resulting system is more probable. In fact whenever a change occurs, the overall entropy of the universe always increases.[18] The second law has (as far as we know) never, ever been violated. In fact the direction of entropy change has been called “time’s arrow”; the forward direction of time is determined by the entropy change. At this point you should be shaking your head. All this cannot possibly be true! First of all, if entropy is always increasing, then was there a time in the past when entropy was 0?[19] Second, are there not situations where entropy decreases and things become more ordered, like when you clean up a room? Finally, given that common sense tells us that time flows in only one direction (to the future), how is it possible that at the atomic and molecular scale all events are reversible?
Probability and Entropy
Before we look at entropy in detail, let us look at a few systems and think about what we already know about probability. For example if you take a deck of cards and shuffle it, which is more probable: that the cards will fall into the order ace, king, queen, jack, 10, 9, etc. for each suit, or that they will end up in some random, jumbled order? Of course the answer is obvious—the random order is much more probable because there are many sequences of cards that count as “random order” but only one that counts as “ordered.” This greater probability is true even though any pre-specified random sequence is just as unlikely as the perfectly ordered one. It is because we care about a particular order that we lump all other possible orders of the cards together as “random” and do not distinguish between them.
We can calculate, mathematically, the probability of the result we care about. To determine the probability of an event (for example, a particular order of cards), we divide the number of outcomes cared about by the total number of possible outcomes. For 52 cards there are 52! (52 factorial, or 52 x 51 x 50 x 49…) ways that the cards can be arranged.[20] This number is ~8.07 x 1067, a number on the same order of magnitude as the number of atoms in our galaxy. So the probability of shuffling cards to produce any one particular order is 1/52! – a very small number indeed. But because the probability is greater than zero, this is an event that can happen. In fact, it must happen eventually, because the probability that any given arrangement of cards will occur is 1. That is a mind bender, but true nevertheless. Highly improbable events occur all the time![21]
This idea of entropy, in terms of probabilities, can help us understand why different substances or systems have different entropies. We can actually calculate entropies for many systems from the formula S = k ln W, where S is the entropy, k is the Boltzmann constant, and W is the number of distinguishable arrangements (or states) that the system has.[22] So the greater the value of W (the number of arrangements), the greater the entropy.
In some cases it is relatively easy to figure out which system has more possible arrangements. For example, in a solid substance such as ice the molecules are fixed in place and can only vibrate. In a liquid, the molecules are free to roam around; it is possible for each molecule to be anywhere within the liquid mass and not confined to one position. In a gas, the molecules are not confined at all and can be found anywhere, or at least anywhere in the container. In general, gases have more entropy than liquids and solids. This so-called positional entropy can be extended to mixtures. In most mixtures (but not all, as we will see in the case of emulsions and colloids) the number of distinguishable arrangements is larger for the mixed compared to the unmixed components. The entropy of a mixture is usually larger.
So let us return to the idea that the direction of change in a system is determined by probabilities. We will consider the transfer of thermal energy (heat) and see if we can make sense of it. First, remember that energy is quantized. So, for any substance at a particular temperature there will be a certain number of energy quanta (recall that at the atomic-molecular level energy is quantized). To make things simpler, we will consider a four-atom solid that contains two quanta of energy. These quanta can be distributed so that a particular atom can have 0, 1, or 2 quanta of energy. You can either calculate or determine by trial and error the number of different possible arrangements of these quanta (there are 10). Remember that W is the number of distinguishable arrangements, so for this system W = 10 and S = k ln 10. Now, what happens if we consider two similar systems, one with 4 quanta and the other with 8 quanta? The system with 4 quanta will be at a lower temperature than the system with 8 quanta. We can also calculate the value of W for the 4-quanta (4-atom) system by considering the maximum number of possible ways to arrange the quanta over the 4 atoms. For the 4-atom, 4-quanta system, W = 35. If we do the same calculation for the 8-quanta, 4-atom system, W = 165. If taken together, the total number of arrangements of the two systems is 35 x 165 = 5775.[23]
But what about temperature? The 4-quanta system is at a lower temperature than the 8-quanta system because the 8-quanta system has more energy. What happens if we put the two systems in contact? Energy will transfer from the hotter (8-quanta) to the colder (4-quanta) system until the temperatures are equal. At this point, each will have 6 quanta (which corresponds to a W of 84). Because there are two systems (each with 6 quanta), the total W for the combined systems is W of 84 x 84 = 7056 states. You will note that 7056 is greater than 5775. There are more distinguishable arrangements of the quanta in the two systems after the energy transfer than before. The final system is more probable and therefore has a higher entropy.
Now you might well object, given that we are working with systems of only a few atoms each. It is easy to imagine that random fluctuations could lead to the movement of quanta from cold to hot, and that is true. That is why the behavior at the nanoscale is reversible. But when we are talking about macroscopic systems, such a possibility quickly becomes increasingly improbable as the number of atoms/molecules increases. Remember a very small drop of water with a weight of 0.05 grams contains approximately 1.8 x 1021 molecules (perhaps you can also calculate the volume of such a drop). Events that are reversible at the nanoscale are irreversible at the macroscopic scale – yet another wacky and counterintuitive fact. It is generally true that we are driven to seek a purpose for why things happen. In the grand scheme of things, the overarching idea that change in the universe is driven simply by the move to more probable states can be difficult to accept,but it is true – even when we consider living systems in the context of their surroundings.[24] The presence of a living system (which is itself highly organized) increases entropy of the Universe as a whole.
Questions
Questions to Answer
- Which has more entropy (in each case, explain your choice):
- A new deck of cards or a shuffled deck?
- Separated dye and water or a mixed-up solution?
- H2O(s) or H2O(l)?
- CaCO3(s) or CaO(s) + CO2(g)?
- H2O(l) (at 25 °C) or H2O(l) (at 50 °C)?
- Do you think that the structure of a compound affects its entropy? Why?
- Predict the relative entropies of diamond and sodium chloride, carbon dioxide, oxygen, and HF. What factors influenced your prediction? Look up the entropies. Were you correct?
Questions to Ponder
- Can you think of any changes that occur that seem to produce more order?
- Why don’t living systems (organisms) violate the second law of thermodynamics?
- Does the second law rule out evolution?
- Does it argue for a supernatural soul running the brain?
5.6 Back to Phase Changes
Let us now return to the situation with solids, liquids, and gases. How do we think about entropy in these systems? Doesn’t a substance become more ordered as we move it from gas to liquid to solid? Clearly the entropy of a solid is lower than that of a liquid, and the entropy of a liquid is lower than that of a gas. We can calculate (or simply look up) how entropies change for materials as they go from gas to liquid to solid. As we have predicted, they decrease. How can a change occur when the entropy of the system decreases (such as ice freezing)? Are we forced to conclude that things we know to happen are impossible according to the second law of thermodynamics? Of course not!
The second law of thermodynamics tells us that for every change that occurs, the entropy of the universe must increase. The problem with this is that we are all well aware of changes where the entropy apparently decreases. How can we resolve this seeming paradox? The answer lies in the fact that for any system the entropy may indeed decrease; water freezing is an example of this phenomenon. For the universe as a whole however (or more easily defined, the system and its surroundings) total entropy must increase. For example, when water freezes, the water molecules form stable interactions (hydrogen bonding interactions). As we have seen previously, the formation of stabilizing interactions means that the potential energy of the system has decreased. Because energy is conserved, this energy must be released to the surroundings as thermal (kinetic) energy. That is, the freezing of water is an exothermic process.
Now we can see the solution to our thermodynamic problem. The reason that the freezing of water does not violate the second law is that even though the system (ice) becomes more ordered and has lower entropy, the energy that is released to the surroundings makes those molecules move faster, which leads to an increase in the entropy of the surroundings. At the freezing point of ice the increase in entropy in the surroundings is greater than the decrease in entropy of the ice! When we consider both system and surroundings, the change in entropy (ΔS) is positive. The second law is preserved (yet again), but to understand why we must actively embrace systems thinking.
5.7 Gibbs (Free) Energy to the Rescue
We must consider changes in entropy for both the system and its surroundings when we predict which way a change will occur, or in which direction a process is thermodynamically favorable. Because it is almost always easier to look at the system than it is to look at the surroundings (after all, we define the system as that part of the universe we are studying), it would be much more convenient to use criteria for change that refer only to the system. Fortunately, there is a reasonably simple way to do this. Let us return to water freezing again and measure the enthalpy change for this process. The thermal energy change for the system, ΔHfreezing, is about –6 kJ/mol. That is, 6 kJ of thermal energy are released into the surroundings for every mole of water that freezes. We can relate this thermal energy release to the entropy change of the surroundings. Entropy is measured in units of J/K (energy/temperature). Because we know how much energy is added to the surroundings, we can calculate the entropy change that this released (enthalpic) energy produces.
Mathematically we can express this as ΔSsurroundings = –ΔHsurroundings/T. And because we know that ΔHsystem = –ΔHsurroundings, or that the energy lost by the system equals minus (–) the energy gained by the surroundings, we can express the entropy change of the surroundings in terms of measurable variables for the system. That is:
ΔSsurroundings = –ΔHsystem / T.
If you recall, we can express the total entropy change (the one relevant for the second law) as ΔStotal = ΔSsystem + ΔSsurroundings. Substituting for the ΔSsurroundings term, we get
ΔStotal = ΔSsystem –ΔHsystem/T. Now we have an equation that involves only variables that relate to the system, which are much easier to measure and calculate. We can rearrange the equation by multiplying throughout by -T, which gives us:
–TΔStotal = ΔHsystem – TΔSsystem
The quantity –TΔStotal has units of energy, and is commonly known as the Gibbs energy change, ΔG (or sometimes as the free energy). The equation is normally written as:
ΔG = ΔH – TΔS.
The Gibbs energy change of a reaction is probably the most important thermodynamic term that you will need to learn about. In most biological and biochemical systems, it is ΔG that is commonly used to determine whether reactions are thermodynamically favorable. It is important to remember that ΔG is a proxy for the entropy change of the universe: if it is negative, universal entropy is increasing (and the reaction occurs); if it is positive, universal entropy would decrease if the reaction occurred (and so it does not). It is possible, however, for reactions with a positive ΔG to occur, but only if they are coupled with a reaction with an even greater negative ΔG (see Chapters 8 and 9).
There are numerous tables of thermodynamic data in most texts and on many websites. Because we often want to use thermodynamic data such as ΔH, ΔS, and ΔG, it is useful to have some reference state. This is known as the standard state and is defined as 298 K temperature, 1 atmosphere pressure, 1M concentrations. When thermodynamic data refer to the standard state they are given the superscript º (nought), so ΔHº, ΔSº, and ΔGº all refer to the standard state. However, we often apply these data at temperatures other than 298 K and although small errors might creep in, the results are usually accurate enough.
What Is Free” About Gibbs Free Energy?
We use ΔG or ΔGº to describe many systems (and especially biological ones) because both the magnitude and sign tell us a lot about how that system behaves. We use ΔG (the Gibbs free energy change) rather than ΔH (the enthalpy change) because ΔG tells us how much energy is actually available to bring about further change (or to do work). In any change some of the energy is lost to the environment as the entropy increases, this dissipated energy cannot be used to do any kind of work and is effectively lost. ΔG differentiates the energy produced from the change from the energy that is lost to the surroundings as increased entropy. As an example, when wood is burned, it is theoretically impossible to use all of the heat released to do work; some of the energy goes to increase the entropy of the system. For any change in the system, some of the energy is always lost in this way to the surroundings. This is why it is impossible to build a machine that is 100% efficient in converting energy from one kind to another (although many have tried–Google “perpetual motion machines” if you don’t believe us). So the term “free energy” doesn’t mean that it is literally free, but rather that it is potentially available to use for further transformations.
When ΔG is negative, we know that the reaction will be thermodynamically favored.[25] The best-case scenario is when ΔH is negative (an exothermic change in which the system is losing energy to the surroundings and becoming more stable), and ΔS is positive (the system is increasing in entropy). Because T is always greater than 0 (in Kelvins), TΔS is also positive and when we subtract this value from ΔH, we get an even larger negative ΔG value. A good example of such a process is the reaction (combustion) of sugar (C6H12O6) with molecular oxygen (O2):
C6H12O6(s) + 6 O2(g) → 6 CO2(g) + 6 H2O(g).
This is an exothermic process and, as you can see from the reaction equation, it results in the production of more molecules than we started with (often a sign that entropy has increased, particularly if the molecules are of a gas).
A process such as this (-ΔH and +ΔS) is thermodynamically favored at all temperatures. On the other hand, an endothermic process (+ΔH) and a decrease in entropy (-ΔS) will never occur as an isolated reaction (but in the real world few reactions are actually isolated from the rest of the universe). For example, a reaction that combined CO2 and H2O to form sugar (the reverse reaction to the combustion reaction above) is never thermodynamically favored because ΔH is positive and ΔS is negative, making ΔG positive at all temperatures. Now you may again find yourself shaking your head. Everyone knows that the formation of sugars from carbon dioxide and water goes on all over the world right now (in plants)! The key here is that plants use energy from the sun, so the reaction is actually:
captured energy + 6 CO2(g) + 6 H2O(g) ⇆ C6H12O6(s) + 6 O2(g) + excess energy.
Just because a process is thermodynamically unfavorable doesn’t mean that it can never occur. What it does mean is that that process cannot occur in isolation; it must be “coupled” to other reactions or processes.
Free Energy and Temperature
So we have two very clear-cut cases that allow us to predict whether a process will occur: where the enthalpy and entropy predict the same outcome. But there are two possible situations where the enthalpy change and the entropy term (TΔS) “point” in different directions. When ΔH is positive and ΔS is positive, and when ΔH is negative while ΔS is negative. When this happens, we need to use the fact that the free energy change is temperature-dependent in order to predict the outcome. Recall that the expression ΔG = ΔH – TΔS depends upon temperature. For a system where the entropy change is positive (+ΔS), an increase in temperature will lead to an increasingly negative contribution to ΔG. In other words, as the temperature rises, a process that involves an increase in entropy becomes more favorable. Conversely, if the system change involves a decrease in entropy, (ΔS is negative), ΔG becomes more positive (and less favorable) as the temperature increases.
| ΔH | ΔS | ΔG |
| Negative
(exothermic) |
Positive
(entropy increases) |
Negative at all temperatures (always thermodynamically favored) |
| Positive
(endothermic) |
Negative
(entropy decreases) |
Positive at all temperatures (never thermodynamically favored) |
| Negative
(exothermic) |
Negative
(entropy decreases) |
Temperature dependent: as the temperature increases ΔG will become more positive and the reaction will become less favored (go backwards) |
| Positive
(endothermic) |
Positive
(entropy increases) |
Temperature dependent: as the temperature increases ΔG will become more negative and the reaction will become favored (go forwards) |
The idea that temperature affects the direction of some processes is perhaps a little disconcerting. It goes against common-sense that if you heat something up a reaction might actually stop and go backwards (rest assured we will come back to this point later). But in fact there are a number of common processes where we can apply this kind of reasoning and find that they make perfect sense.
Up to this point, we have been considering physical changes to a system—populations of molecules going from solid to liquid or liquid to gaseous states (and back). Not really what one commonly thinks of as chemistry, but the fact is that these transformations involve the making and breaking of interactions between molecules. We can therefore consider phase transitions as analogous to chemical reactions, and because they are somewhat simpler, develop a logic that applies to both processes. So let us begin by considering the phase change/reaction system
H2O (liquid) ⇌ H2O (gas).
We use a double arrow ⇌ to indicate that, depending upon the conditions the reaction could go either to the right (boiling) or to the left (condensing). So, let us assume for the moment that we do not already know that water boils (changes from liquid to gas) at 100 ºC. What factors would determine whether the reaction H2O(liquid) ⇌ H2O(gas) favors the liquid or the gaseous state at a particular temperature? As we have seen, the criterion for whether a process will “go” at a particular temperature is ΔG. We also know that the free energy change for a reaction going in one direction is the negative of the ΔG for the reaction going in the opposite direction. So that the ΔG for the reaction: H2O(liquid) ⇌ H2O(gas) is –ΔG for the reaction H2O(gas) ⇌ H2O(liquid).
When water boils, all the intermolecular attractions between the water molecules must be overcome, allowing the water molecules to fly off into the gaseous phase. Therefore, the process of water boiling is endothermic (ΔHvaporization = +40.65 kJ/mol); it requires an energy input from the surroundings (when you put a pot of water on the stove you have to turn on the burner for it to boil). When the water boils, the entropy change is quite large (ΔSvaporization = 109 J/mol K), as the molecules go from being relatively constrained in the liquid to gas molecules that can fly around. At temperatures lower than the boiling point, the enthalpy term predominates and ΔG is positive. As you increase the temperature in your pan of water, eventually it reaches a point where the contributions to ΔG of ΔH and TΔS are equal. That is, ΔG goes from being positive to negative and the process becomes favorable. At the temperature where this crossover occurs ΔG = 0 and ΔH = TΔS. At this temperature (373 K, 100 ºC) water boils (at 1 atmosphere). At temperatures above the boiling point, ΔG is always negative and water exists predominantly in the gas phase. If we let the temperature drop below the boiling point, the enthalpy term becomes predominant again and ΔG for boiling is positive. Water does not boil at temperatures below 100 ºC at one atmosphere.[26]
Let us now consider a different phase change, such as water freezing. When water freezes, the molecules in the liquid start to aggregate and form hydrogen bonding interactions with each other, and energy is released to the surroundings (remember it is this energy that is responsible for increasing the entropy of the surroundings). Therefore ΔH is negative: freezing is an exothermic process (ΔHfusion = – 6 kJ/mol).[27] Freezing is also a process that reduces the system’s entropy. When water molecules are constrained, as in ice, their positional entropy is reduced. So, water freezing is a process that is favored by the change in enthalpy and disfavored by the change in entropy. As the temperature falls, the entropy term contributes less to ΔG, and eventually (at the crossover point) ΔGfusion goes to zero and then becomes negative. The process becomes thermodynamically favored. Water freezes at temperatures below 0 ºC. At temperatures where phase changes take place (boiling point, melting point), ΔG = 0. Furthermore, if the temperature were kept constant, there would be no observable change in the system. We say that the system is at equilibrium; for any system at equilibrium, ΔG = 0.
Questions
Questions to Answer
- For each of these processes, give the change in entropy of the system, the direction of thermal energy transfer (the sign of ΔH), the change in entropy of the surroundings, and the change in entropy of the universe:
- Water freezing at -10 °C
- Water boiling at 110 °C
- For each of these processes predict the sign of change in entropy (ΔS) of the system, the direction of thermal energy transfer (the sign of ΔH), and the sign of the Gibbs free energy change, ΔG. What does the sign of ΔG tell you?
- Water freezing at -10 °C; Water boiling at 110 °C
- Water boiling at -10 °C; Water freezing at 110 °C
Questions to Ponder
- Why do we denote excess energy as a product of this equation? captured energy + 6 CO2(g) + 6 H2O(g) ⇆ C6H12O6(s) + 6 O2(g) + excess energy.
- What other processes do you know that must be coupled to external energy sources to make them go?
- Instead of talking about the temperature of an isolated atom or molecule, we talk about its kinetic energy. ↵
- We can ignore gravitational effects because at the molecular level they are many orders of magnitude weaker than the forces between atoms and molecules. ↵
- actually v(bar) is the root mean squared velocity of the gas particles,a measure that is similar to the mean, but makes the direction of the particles irrelevant. ↵
- We can also, for all practical purposes, ignore the fact that E = mc2; the conversions between energy and matter are insignificant for chemical processes. ↵
- Although this distribution of speeds of atoms was first derived mathematically, it is possible to observe experimentally that atoms in a gas are moving at different speeds. ↵
- Interestingly, this is like our approach to the decay of unstable atoms. We cannot predict when a particular atom will decay, but in a large enough population, we can very accurately predict the number of atoms per second that will decay. ↵
- We use average speed and velocity to describe the motion of the particles in a gas, but it is more accurate to use the root mean square (rms) of the velocity, that is, the square root of the average velocity. However, for our purposes average speed (or velocity) is good enough. ↵
- Translational energies are also quantized but the quanta are so small that in practice we do not need to worry about that. ↵
- There are a number of different energy units, including calories, but they are all measures of the same thing, so we will stick to joules here. ↵
- Alternatively in microwave ovens, the water molecules gain energy by absorbing microwave radiation which makes them rotate. When they collide with other molecules this energy can also be transformed into vibrations and translations, and the temperature of the water heats up. ↵
- The situation on planets like Venus and Jupiter is rather more complex. ↵
- The boundary between a system and surroundings depends on how you define the system. It can be real (as in the beaker) or imaginary (as in some ecosystems). In biological systems, the boundary may be the cell wall, or the boundary between the organism and its surroundings (e.g., skin). ↵
- The only exception would be cryptobiotic systems, like the tardigrads mentioned earlier. ↵
- Remember that London dispersion forces fall off as 1/r6, where r is the distance between the molecules. ↵
- In fact, we should say mass-energy here, but because most chemical and biological systems do not operate under the high-energy situations required for mass to be converted to energy we don’t need to worry about that (for now). ↵
- Or U if you are a physicist. This is an example of how different areas sometimes seem to conspire to make things difficult by using different symbols and sign conventions for the same thing. We will try to point out these instances when we can. ↵
- One important point to note is that this relationship only works when the thermal energy is used to increase the kinetic energy of the molecules—that is, to raise the temperature. At the boiling point or freezing point of a liquid the energy is used to break the attractions between particles and the temperature does not rise. ↵
- This is another example of the different ways that the same process is described. In chemistry we usually describe osmosis as movement from a solution of low concentration to high (where we are referring to the concentration of the solute). In biology osmosis is often described as movement from high concentration (of water) to low. These two statements mean exactly the same thing even though they appear to be saying the opposite of each other. ↵
- One of many speculations about the relationship between the big bang and entropy; http://chronicle.uchicago.edu/041118/entropy.shtml ↵
- http://www.schuhmacher.at/weblog/52cards.html ↵
- A realistic understanding of the probability of something happening is a great asset (but would put the gambling and lottery industries, and perhaps part of the investment community, out of business). Listen to: http://www.wnyc.org/shows/radiolab/episodes/2009/09/11 ↵
- or Ω in some texts. ↵
- We multiply, rather than add W when we combine systems. ↵
- A great lecture by Richard Feynmann on this topic: http://research.microsoft.com/apps/tools/tuva/#data=5%7C0%7C%7Cd88d1dbd-a736-4c3f-b832-2b0df62e4eca%7C%7C ↵
- Many people use the term spontaneous, but this is misleading because it could make people think that the reaction happens right away. In fact, ΔG tells us nothing about when the process will happen, only that it is thermodynamically favored. As we will see later, the rate at which a process occurs is governed by other factors. ↵
- So why, you might ask, does water evaporate at temperatures lower than 100 ºC? We will come to that soon. ↵
- This is another rather counterintuitive idea, but remember that to freeze something you have to take heat away (for example, in a refrigerator). ↵

