Even as he articulated his planetary model of the atom, Rutherford was aware that there were serious problems with it. For example because like charges repel and unlike charges attract, it was not at all clear why the multiple protons in the nuclei of elements heavier than hydrogen did not repel each other and cause the nuclei to fragment. What enables them to stay so close to each other? On the other hand, if electrons are orbiting the nucleus like planets around the Sun, why don’t they repel each other, leading to quite complex and presumably unstable orbits? Why aren’t they ejected spontaneously and why doesn’t the electrostatic attraction between the positively-charged nucleus and the negatively-charged electrons result in the negatively-charged electrons falling into the positively charged nucleus? Assuming that the electrons are moving around the nucleus, they are constantly accelerating (changing direction). If you know your physics, you will recognize that (as established by J.C. Maxwell – see below) a charged object emits radiation when accelerating.^[1]  As the electron orbits the nucleus this loss of energy will lead it to spiral into the nucleus – such an atom would not be stable. But, as we know, most atoms are generally quite stable.

So many questions and so few answers! Clearly Rutherford’s model was missing something important and assumed something that cannot be true with regard to forces within the nucleus, the orbital properties of electrons, and the attractions between electrons and protons. To complete this picture leads us into the weird world of quantum mechanics.

2.1 Light and Getting Quantum Mechanical

While Rutherford and his colleagues worked on the nature of atoms, other scientists were making significant progress in understanding the nature of electromagnetic radiation, that is, light. Historically, there had been a long controversy about the nature of light, with one side arguing that light is a type of wave, like sound or water waves, traveling through a medium like air or the surface of water and the other side taking the position that light is composed of particles. Isaac Newton called them corpuscles. There was compelling evidence to support both points of view, which seemed to be mutually exclusive, and the attempt to reconcile these observations into a single model proved difficult.

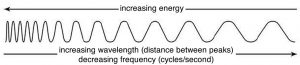
By the end of the 1800s, most scientists had come to accept a wave model for light because it better explained behaviors such as interference^[2] and diffraction,^[3] the phenomena that gives rise to patterns when waves pass through or around objects that are of similar size to the wave itself. James Clerk Maxwell (1831–1879) developed the electromagnetic theory of light, in which visible light and other forms of radiation, such as microwaves, radio waves, X-rays, and gamma rays, were viewed in terms of perpendicular electric and magnetic fields. A light wave can be described by defining its frequency (ν) and its wavelength (λ). For all waves, the frequency times its wavelength equals the velocity of the wave. In the case of electromagnetic waves, λν = c, where c is the velocity of light.

Although the wave theory explained many of the properties of light, it did not explain them all. Two types of experiments in particular gave results that did not appear to be compatible with the wave theory. The first arose during investigations by the German physicist Max Planck (1858–1947) of what is known as black body radiation. In these studies, an object heated to a particular temperature emits radiation. Consider your own body, which typically has a temperature of approximately 98.6 ºF or 36 ºC. Your body emits infrared radiation that can be detected by some cameras.^[4] Some animals, like snakes, have infrared detectors that enable them to locate their prey—typically small, warm-blooded, infrared-light-emitting mammals.^[5] Because mammals tend to be warmer than their surroundings, infrared vision can be used to find them in the dark or when they are camouflaged.

Planck had been commissioned by an electric power company to produce a light bulb that emitted the maximum amount of light using the minimum amount of energy. In the course of this project he studied how the color of the light emitted (a function of its wavelength) changed as a function of an object’s (such as a light bulb filament) temperature. We can write this relationship as λ (wavelength) = f(t) where t = temperature and f indicates “function of.”  To fit his data Planck had to invoke a rather strange and non-intuitive idea, namely that matter absorbs and emits energy only in discrete chunks, which he called quanta. These quanta occurred in multiples of E (energy) = hν, where h is a constant, now known as Planck’s constant, and ν is the frequency of light. Planck’s constant is considered one of the fundamental numbers that describes our universe.^[6] The physics that uses the idea of quanta is known as quantum mechanics.

One problem with Planck’s model, however, is that it disagreed with predictions of classical physics; in fact as the frequency of the light increased, his measurements diverged more and more from the predictions of the then current, wave-based theory.^[7]  This divergence between classical theory and observation became known, perhaps over-dramatically, as the ultraviolet catastrophe. It was a catastrophe for the conventional theory because there was no obvious way to modify classical theories to explain Planck’s observations; this was important because Planck’s observations were reproducible and accurate. Once again, we see an example of the rules of science: a reproducible discrepancy, even if it seems minor, must be addressed or the theory must be considered either incomplete or just plain wrong.

The idea that atoms emit and absorb energy only in discrete packets is one of the most profound and revolutionary discoveries in all of science, and set the stage for a radical rethinking of the behavior of energy and matter on the atomic and subatomic scales. Planck himself proposed the idea with great reluctance and spent a great deal of time trying to reconcile it with classical theories of light. In the next section we will see how this property can be used to identify specific types of atoms, both in the laboratory and in outer space.

2.2 Taking Quanta Seriously

In 1905, Albert Einstein used the idea of quanta to explain the photoelectric effect, which was described by Philipp Lenard (1862-1947). The photoelectric effect occurs when light shines on a metal plate and electrons are ejected, creating a current.^[8] Scientists had established that there is a relationship between the wavelength of the light used, the type of metal the plate is made of, and whether or not electrons are ejected. It turns out that there is a threshold wavelength (energy) of light that is characteristic for the metal used, beyond which no electrons are ejected. The only way to explain this is to invoke the idea that light comes in the form of particles, known as photons, that also have a wavelength and frequency (we know: this doesn’t make sense, but bear with us for now). The intensity of the light is related to the number of photons that pass by us per second, whereas the energy per photon is dependent upon its frequency or wavelength, because wavelength and frequency of light are related by the formula λν = c where c is the speed of light in a vacuum, is a constant and equal to ~3.0 x 10⁸ m/s. The higher the frequency ν (cycles per second, or Hertz), the shorter the wavelength λ (length per cycle) and the greater the energy per photon. Because wavelength and frequency are inversely related–that is, as one goes up the other goes down– energy is directly related to frequency by the relationship E = hν or inversely related to the wavelength E= hc/λ, where h is Planck’s constant. So radiation with a very short wavelength, such as x rays (λ= ~10^–10 m) and ultraviolet light (between 10^-7 to 10^-8 m), have much more energy per particle than long wavelength radiation like radio and microwaves (λ= ~10³ m). This is why we (or at least most of us) do not mind being surrounded by radio waves essentially all the time yet we closely guard our exposure to gamma rays, X-rays, and UV light; their much higher energies cause all kinds of problems with our chemistry, as we will see later.

Because of the relationship between energy and wavelength (λν = c), when you shine long-wavelength, low energy, such as infrared, but high intensity (many photons per second) light on a metal plate, no electrons are ejected. But when you shine short-wavelength, high energy (such as ultraviolet or x rays) but low intensity (few photons per second) light on the plate, electrons are ejected. Once the wavelength is short enough (or the energy is high enough) to eject electrons, increasing the intensity of the light now increases the number of electrons emitted. An analogy is with a vending machine that can only accept quarters; you could put nickels or dimes into the machine all day and nothing will come out. The surprising result is that the same total amount of energy can produce very different effects. Einstein explained this observation (the photoelectric effect) by assuming that only photons with “enough energy” could eject an electron from an atom. If photons with lower energy hit the atom no electrons are ejected – no matter how many photons there are.^[9] You might ask: Enough energy for what? The answer is enough energy to overcome the attraction between an electron and the nucleus. In the photoelectric effect, each photon ejects an electron from an atom on the surface of the metal. These electrons exist somewhere within the atoms that make up the metal (we have not yet specified where) but it takes energy to remove them and the energy is used to overcome the force of attraction between the negative electron and the positive nucleus.

Now you should be really confused, and that is a normal reaction! On one hand we were fairly convinced that light acted as a wave but now we see some of its behaviors can be best explained in terms of particles. This dual nature of light is conceptually difficult for most normal people because it is completely counter intuitive. In our macroscopic world things are either particles, such as bullets, balls, coconuts, or waves (in water); they are not—no, not ever—both. As we will see, electromagnetic radiation is not the only example of something that has the properties of both a wave and a particle; this mix of properties is known as wave–particle duality. Electrons, protons, and neutrons also display wavelike properties. In fact, all matter has a wavelength, defined by Louis de Broglie (1892–1987), by the equation λ = h/mν where mv is the object’s momentum (mass x velocity) and h is Planck’s constant. For heavy objects, moving at slow speeds, the wavelength is very, very small, but it becomes a significant factor for light objects moving fast, such as electrons. Although light and electrons can act as both waves and as particles, it is perhaps better to refer to them as quantum mechanical particles, a term that captures all features of their behavior and reminds us that they are weird! Their behavior will be determined by the context in which we study (and think of) them.

2.3 Exploring Atomic Organization Using Spectroscopy^[10]

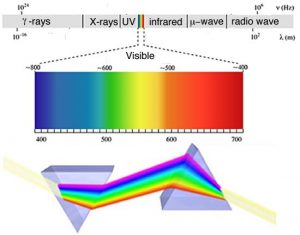
As we will often see, there are times when an old observation suddenly fits into and helps clarify a new way of thinking about a problem or process. In order to understand the behavior of electrons within atoms scientists brought together a number of such observations. The first observation has its roots in understanding the cause of rainbows. The scientific explanation of the rainbow is based on the fact that light of different wavelengths is bent through different angles (refracted) when it passes through an air–water interface. When sunlight passes through approximately spherical water droplets, it is refracted at the air–water interface, partially reflected (note the difference) from the backside of the water droplet, and then refracted again as it leaves the droplet. The underlying fact that makes rainbows possible is that sunlight is composed of photons with an essentially continuous distribution of visible wavelengths. Isaac Newton illustrated this nicely by using a pair of prisms to show that white light could be separated into light of many different colors by passing it through a prism and then recombined back into white light by passing it through a second prism. On the other hand, light of a single color remained that color, even after it passed through a second prism.

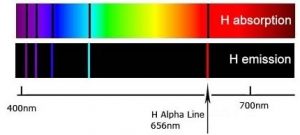
When a dense body, like the Sun or the filament of an incandescent light bulb, is heated, it emits light of many wavelengths (colors)—essentially all wavelengths in the visible range. However, when a sample of an element or mixture of elements is heated, for example in a flame provided by a Bunsen burner, it emits light of only very particular wavelengths. The different wavelengths present in the emitted light can be separated from one another using a prism to produce what is known as an emission spectra. When projected on a screen these appear as distinct, bright-colored lines, known emission lines. In a complementary manner, if white light, which consists of a continuous distribution of wavelengths of light, is passed through a cold gaseous element the same wavelengths that were previously emitted by the heated element will be absorbed, while all other wavelengths will pass through unaltered. By passing the light through a prism we can see which wavelengths of light have been absorbed by the gas. We call these dark areas “absorption” lines within the otherwise continuous spectrum. The emission and absorption wavelengths for each element the same and unique for each element. Emission and absorption phenomenon provide a method (spectroscopy) by which the absorbance or emission of specific wavelengths of light by can be is used to study the composition and properties of matter. Scientists used spectroscopic methods to identify helium, from the Greek “sun”, in the Sun before it was isolated on Earth.

In the 1800s, it became increasingly clear that each element, even the simplest, hydrogen, has a distinctive and often quite complex emission/absorption spectra. In 1855 Johann Balmer (1825-1898) calculated the position of the lines in the visible region. In 1888 Johannes Rydberg (1854-1919) extended those calculations to the entire spectrum. These calculations, however, were based on an empirical formula and it was unclear why this formula worked or what features of the atom it was based on—this made the calculations rather unsatisfying. Although useful, they provided no insight into the workings of atoms.

Making sense of spectra:

How do we make sense of these observations? Perhaps the most important clue is again the photoelectric effect; that is, the observation that illuminating materials with light can in some circumstances lead to the ejection of electrons. This suggests that it is the interactions between light and the electrons in atoms that are important. Using this idea and the evidence from the hydrogen spectra Niels Bohr (1885-1962) proposed a new model for the atom His first hypothesis was that the electrons within an atom can only travel along certain orbits at a fixed distance from the nucleus, each orbit corresponding to a specific energy. The second idea was that electrons can jump from one orbit to another, but this jump requires either the capture (absorption) or release (emission) of energy, in the form of a photon. An electron can move between orbits only if a photon of exactly the right amount of energy is absorbed (lower to higher) or emitted (higher to lower). Lower (more stable) orbits are often visualized as being closer to the nucleus whereas higher, less stable and more energetic orbits are further away. Only when enough energy is added in a single packet is the electron removed completely from the atom, leaving a positively-charged ion (an ion is an atom or molecule that has a different number of protons and electrons) and a free electron. Because the difference in energy between orbits is different in different types of atoms, moving electrons between different orbits requires photons carrying different amounts of energy (different wavelengths).

Bohr’s model worked well for hydrogen atoms; in fact, he could account for and accurately calculate the wavelengths for all of hydrogen’s observed emission/absorption lines. These calculations involved an integer quantum number that corresponded to the different energy levels of the orbits.^[11] Unfortunately, this model was not able to predict the emission/absorption spectrum for any other element, including helium and certainly not for any molecule. Apparently Bohr was on the right track—because every element does have a unique spectrum and therefore electrons must be transitioning from one energy level to another—but his model was missing something important. It was not at all clear what restricted electrons to specific energy levels. What happens in atoms with more than one electron? Where are those electrons situated and what governs their behavior and interactions? It is worth remembering that even though the Bohr model of electrons orbiting the nucleus is often used as a visual representation of an atom, it is not correct. Electrons do not circle the nucleus in defined orbits. Bohr’s model only serves as an approximate visual model for appearance of an atom–it is not how electrons actually behave!

2.4 Beyond Bohr

Eventually, as they considered the problems with the Bohr model, scientists came back to the idea of the wave–particle duality as exemplified by the photon. If light (electromagnetic radiation), which was classically considered to be a wave, could have the properties of a particle, then perhaps matter, classically considered as composed of particles, could have the properties of waves, at least under conditions such as those that exist within an atom. Louis De Broglie (1892–1987) considered this totally counterintuitive idea in his Ph.D. thesis. De Broglie used Planck’s relationship between energy and frequency (E = hn), the relationship between frequency and wavelength (c = λn), and Einstein’s relationship between energy and mass (E = mc2) to derive a relationship between the mass and wavelength for any particle (including photons).^[12] You can do this yourself by substituting into these equations, to come up with λ = h/mv, where mv is the momentum of a particle with mass m and velocity v. In the case of photons, v = c, the velocity of light.

Although the math involved in deriving the relationship between momentum (mv) of a particle and its wavelength λ is simple, the ideas behind it are most certainly not. It is even more difficult to conceptualize the idea that matter, such as ourselves, can behave like waves, and yet this is consistent with a broad range of observations. We never notice the wavelike properties of matter because on the macroscopic scale, the wavelength associated with a particular object is so small that it is negligible. For example, the wavelength of a baseball moving at 100 m/s is much smaller than the baseball itself. It is worth thinking about what you would need to know to calculate it. At the atomic scale, however, the wavelengths associated with particles are similar to their size, meaning that the wave nature of particles such as electrons cannot be ignored; their behavior cannot be described accurately by models and equations that treat them as simple particles. The fact that a beam of electrons can undergo diffraction, a wave-like behavior provides evidence of this idea.

Certainty and Uncertainty

Where is a wave located? The answer is not completely obvious. You might think it would be easier to determine where a particle is, but things get complicated as they get smaller and smaller. Imagine that we wanted to view an electron within an atom using some type of microscope, in this case, an imaginary one with unlimited resolution. To see something, photons have to bounce or reflect off it and then enter our eye, be absorbed by a molecule in a retinal cell, and start a signal to our brain where that signal is processed and interpreted. When we look at macroscopic objects, their interactions with light have little effect on them. For example, objects in a dark room do not begin to move just because you turn the lights on! Obviously the same cannot be said for atomic-scale objects; we already know that a photon of light can knock an electron completely out of an atom (the photoelectric effect). Now we come to another factor: the shorter the wavelength of light we use, the more accurately we can locate an object.^[13] Remember, however, that wavelength and energy are related: the shorter the wavelength the greater its energy. To look at something as small as an atom or an electron we have to use electromagnetic radiation of a wavelength similar to the size of the electron. We already know that an atom is about 10^-10 m in diameter, so electrons are presumably much smaller. Let us say that we use gamma rays, a form of electromagnetic radiation, whose wavelength is ~10^–12 m. But radiation of such short wavelength carries lots of energy, so these are high-energy photons. When such a high-energy photon interacts with an electron, it dramatically perturbs the electron’s position and motion. That is, if we try to measure where an electron is, we perturb it by the very act of measurement. The act of measurement introduces uncertainty and this uncertainty increases the closer we get to the atomic molecular scale.

This idea was first put forward explicitly by Werner Heisenberg (1901-1976) and is known as the Heisenberg Uncertainty Principle. According to the uncertainty principle, we can estimate the uncertainty in a measurement using the formula Δmv × Δx > h/2π, where Δ mv is the uncertainty in the momentum of the particle (mass times velocity or where it is going and how fast), Δx is the uncertainty in its position in space (where it is at a particular moment), and h is Planck’s constant now divided by 2π. If we know exactly where the particle is (Δx = 0) then we have absolutely no information about its velocity, which means we do not know how fast or in what direction it is going. Alternatively, if we know its momentum exactly (Δmv = 0), that is, we know exactly how fast and in which direction it is going, we have no idea whatsoever where it is! The end result is that we cannot know exactly where an electron is without losing information on its momentum, and vice versa. This has lots of strange implications. For example, if we know the electron is within the nucleus (Δx ~1.5 x 10^–14 m), then we have very little idea of its momentum (how fast and where it is going). These inherent uncertainties in the properties of atomic-level systems are one of their key features. For example, we can estimate some properties very accurately but we cannot know everything about an atomic/molecular-level system at one point in time. This is a very different perspective from the one it replaced, which was famously summed up by Pierre-Simon Laplace (1749–1827), who stated that if the positions and velocities of every object in the universe were known, the future would be set:

We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes. — Pierre-Simon Laplace (1745-1827)

It turns out that a major flaw in Bohr’s model of the atom was that he attempted to define both the position of an electron (a defined orbit) and its energy, or at least the energy difference between orbits, at the same time. Although such a goal seems quite reasonable and would be possible at the macroscopic level, it simply is not possible at the atomic level. The wave nature of the electron makes it impossible to predict exactly where that electron is if we also know its energy level. In fact, we do know the energies of electrons very accurately because of the evidence from spectroscopy. We will consider this point again later in this chapter.

2.5 Organizing Elements: Introduction to the Periodic Table

Up to this point we have made a number of unjustified assumptions. We have talked about elements but we have not explicitly specified how they are different, so let us do that now. If we start with hydrogen we characterized it by the presence of one proton in the nucleus and one electron surrounding it. Atoms are always neutral, which means that the number of positively-charged particles is equal to the number of negatively-charged particles, and charges come in discrete, equal, and opposite units. The presence of one proton and one electron defines a hydrogen atom but the world is a little more complex than that. A hydrogen atom may also contain one or two neutrons in its nucleus. A neutron can be considered, with the forgiveness of physicists, a proton, an electron, and an uncharged neutrino, and so it is electrically neutral. Neutrons are involved in the strong nuclear force and become increasingly important as the element increases in atomic number. In hydrogen, the neutrons (if they are present) have rather little to do, but in heavier elements the strong nuclear force is critical in holding the nucleus together, because at short distances this force is ~100 times stronger than the electrostatic repulsion between positively charged protons, which is why nuclei do not simply disintegrate. At the same time, the strong force acts over a very limited range, so when particles are separated by more than about 2 x 10^-15 m (2 femtometers or fm), we can ignore it.

As we add one proton after another to an atom, which we can do in our minds, and which occurs within stars and supernova, in a rather more complex manner, we generate the various elements. The number of protons determines the elemental identity of an atom, whereas the number of neutrons can vary. Atoms of the same element with different numbers of neutrons are known as isotopes of that element. Each element is characterized by a distinct, whole number (1, 2, 3, …) of protons and the same whole number of electrons. An interesting question emerges here: is the number of possible elements infinite? And if not, why not? Theoretically, it might seem possible to keep adding protons (and neutrons and electrons) to produce a huge number of different types of atoms. However, as Rutherford established, the nucleus is quite small compared to the atom as a whole, typically between one and ten femtometers in diameter. As we add more and more protons (and neutrons) the size of the nucleus exceeds the effective range of the strong nuclear force (< 2 fm), and the nucleus becomes unstable. As you might expect, unstable nuclei break apart (nuclear fission), producing different elements with smaller numbers of protons, a process that also releases tremendous amounts of energy. Some isotopes are more stable than others, which is why the rate of their decay, together with a knowledge of the elements that they decay into can be used to calculate the age of rocks and other types of artifacts.^[14]

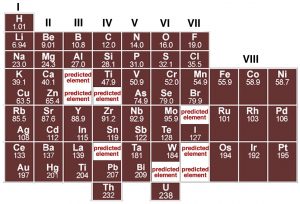
Each element is defined by the number of protons in the nucleus, and as such is different from every other element. In fact, careful analysis of different elements reveals that there are periodicities (repeating patterns) in the properties of elements. Although John Dalton produced a table of elements with their atomic weights in 1805, it was only when Dimitri Mendeleev (1834–1907) tried to organize the elements in terms of their chemical and physical properties that some semblance of order began to emerge. Mendeleev, a Russian chemistry professor, was frustrated by the lack of organization of chemical information, so he decided to write his own textbook (not unlike your current authors). At the time, scientists had identified about 60 elements and established their masses relative to hydrogen. Scientists had already noticed that the elements display repeating patterns of behavior: and that some elements have very similar properties. It was Mendeleev’s insight that these patterns could be used as a guide for arranging the elements in a systematic way. In his periodic table, published in 1869, he placed elements in order of increasing atomic weight in repeating rows from left to right; elements with similar chemical properties were placed in vertical columns (known as groups).

Although several other scientists were working on schemes to show patterns in elemental behavior, it was Mendeleev’s arrangement that emerged as the basis for the modern periodic table, not only because of the way he arranged the elements but also for what he left out and what he changed. For example he was so sure about the underlying logic of his table that where certain elements seemed out of place, based, for example, on their reported atomic weights, such as tellurium and iodine, he reversed them and he turned out to be correct. Where Mendeleev predicted elements should be, he left gaps in his table to accommodate them. Subsequently, scientists discovered these missing elements (for example germanium, gallium, and scandium). In fact, we now know that it is not atomic weight (that is the number of protons and neutrons) but rather atomic number, Z, (the number of protons and electrons) that increases periodically. This explains why tellurium (atomic mass 127.6, Z = 52) must come before iodine (atomic mass 126.9, Z = 53). The important point to note is that although the modern periodic table is arranged in order of increasing number of protons and electrons, the repetition and patterns that emerge are the property of the electrons, their arrangements, and energies. This is our next subject.

2.6 Orbitals, Electron Clouds, Probabilities, and Energies

Our current working model of the atom is based on quantum mechanics that incorporate the ideas of quantized energy levels, the wave properties of electrons, and the uncertainties associated with electron location and momentum. If we know their energies, which we do, then the best we can do is to calculate a probability distribution that describes the likelihood of where a specific electron might be found, if we were to look for it. If we were to find it, we would know next to nothing about its energy, which implies we would not know where it would be in the next moment. We refer to these probability distributions by the anachronistic, misleading, and Bohrian term orbitals. Why misleading? Because to a normal person, the term orbital implies that the electron actually has a defined and observable orbit, something that is simply impossible to know (can you explain why?)

Another common and often useful way to describe where the electron is in an atom is to talk about the electron probability density or electron density for short. In this terminology, electron density represents the probability of an electron being within a particular volume of space; the higher the probability the more likely it is to be in a particular region at a particular moment. Of course you can’t really tell if the electron is in that region at any particular moment because if you did you would have no idea of where the electron would be in the next moment.

Erwin Schrödinger (1887–1961) developed, and Max Born (1882–1970) extended, a mathematical description of the behavior of electrons in atoms. Schrödinger used the idea of electrons as waves and described each atom in an element by a mathematical wave function using the famous Schrödinger equation (HΨ = EΨ). We assume that you have absolutely no idea what either HΨ or EΨ are but don’t worry—you don’t really need to. The solutions to the Schrödinger equation are a set of equations (wave functions) that describe the energies and probabilities of finding electrons in a region of space. They can be described in terms of a set of quantum numbers; recall that Bohr’s model also invoked the idea of quantum numbers. One way to think about this is that almost every aspect of an electron within an atom or a molecule is quantized, which means that only defined values are allowed for its energy, probability distribution, orientation, and spin. It is far beyond the scope of this book to present the mathematical and physical basis for these calculations, so we won’t pretend to try. However, we can use the results of these calculations to provide a model for the arrangements of electrons in an atom using orbitals, which are mathematical descriptions of the probability of finding electrons in space and determining their energies. Another way of thinking about the electron energy levels is that they are the energies needed to remove that electron from the atom or to move an electron to a “higher” orbital. Conversely, this is the same amount of energy released when an electron moves from a higher energy to a lower energy orbital. Thinking back to spectroscopy, these energies are also related to the wavelengths of light that an atom will absorb or release. Let us take a look at some orbitals, their quantum numbers, energies, shapes, and how we can used them to explain atomic behavior.

Examining Atomic Structure Using Light: On the Road to Quantum Numbers

J.J. Thompson’s studies (remember them?) suggested that all atoms contained electrons. We can use the same basic strategy in a more sophisticated way to begin to explore the organization of electrons in particular atoms. This approach involves measuring the amount of energy it takes to remove electrons from atoms. This is known as the element’s ionization energy which in turn relates directly back to the photoelectric effect.

All atoms are by definition electrically neutral, which means they contain equal numbers of positively- and negatively-charged particles (protons and electrons). We cannot remove a proton from an atom without changing the identity of the element because the number of protons is how we define elements, but it is possible to add or remove an electron, leaving the atom’s nucleus unchanged. When an electron is removed or added to an atom the result is that the atom has a net charge. Atoms (or molecules) with a net charge are known as ions, and this process (atom/molecule to ion) is called ionization. A positively charged ion (called a cation) results when we remove an electron; a negatively charged ion (called an anion) results when we add an electron. Remember that this added or removed electron becomes part of, or is removed from, the atom’s electron system.

Now consider the amount of energy required to remove an electron. Clearly energy is required to move the electron away from the nucleus that attracts it. We are perturbing a stable system that exists at a potential energy minimum – that is the attractive and repulsive forces are equal at this point. We might naively predict that the energy required to move an electron away from an atom will be the same for each element. We can test this assumption experimentally by measuring what is called the ionization potential. In such an experiment, we would determine the amount of energy (in kilojoules per mole of molecules) required to remove an electron from an atom. Let us consider the situation for hydrogen (H). We can write the ionization reaction as:

H (gas) + energy → H⁺ (gas) + e^–.^[15]

What we discover is that it takes 1312 kJ to remove a mole of electrons from a mole of hydrogen atoms. As we move to the next element, helium (He) with two electrons, we find that the energy required to remove an electron from helium is 2373 kJ/mol, which is almost twice that required to remove an electron from hydrogen!

Let us return to our model of the atom. Each electron in an atom is attracted to all the protons, which are located in essentially the same place, the nucleus, and at the same time the electrons repel each other. The potential energy of the system is modeled by an equation where the potential energy is proportional to the product of the charges divided by the distance between them. Therefore the energy to remove an electron from an atom should depend on the net positive charge on the nucleus that is attracting the electron and the electron’s average distance from the nucleus. Because it is more difficult to remove an electron from a helium atom than from a hydrogen atom, our tentative conclusion is that the electrons in helium must be attracted more strongly to the nucleus. In fact this makes sense: the helium nucleus contains two protons, and each electron is attracted by both protons, making them more difficult to remove. They are not attracted exactly twice as strongly because there are also some repulsive forces between the two electrons.

The size of an atom depends on the size of its electron cloud, which depends on the balance between the attractions between the protons and electrons, making it smaller, and the repulsions between electrons, which makes the electron cloud larger.^[16] The system is most stable when the repulsions balance the attractions, giving the lowest potential energy. If the electrons in helium are attracted more strongly to the nucleus, we might predict that the size of the helium atom would be smaller than that of hydrogen. There are several different ways to measure the size of an atom and they do indeed indicate that helium is smaller than hydrogen. Here we have yet another counterintuitive idea: apparently, as atoms get heavier (more protons and neutrons), their volume gets smaller!

Given that i) helium has a higher ionization energy than hydrogen and ii) that helium atoms are smaller than hydrogen atoms, we infer that the electrons in helium are attracted more strongly to the nucleus than the single electron in hydrogen. Let us see if this trend continues as we move to the next heaviest element, lithium (Li). Its ionization energy is 520 Kj/mol. Oh, no! This is much lower than either hydrogen (1312 kJ/mol) or helium (2373 kJ/mol). So what do we conclude? First, it is much easier (that is, requires less energy) to remove an electron from Li than from either H or He. This means that the most easily removed electron in Li is somehow different than are the most easily removed electrons of either H or He. Following our previous logic we deduce that the “most easily removable” electron in Li must be further away (most of the time) from the nucleus, which means we would predict that a Li atom has a larger radius than either H or He atoms. So what do we predict for the next element, beryllium (Be)? We might guess that it is smaller than lithium and has a larger ionization energy because the electrons are attracted more strongly by the four positive charges in the nucleus. Again, this is the case. The ionization energy of Be is 899 kJ/mol, larger than Li, but much smaller than that of either H or He. Following this trend the atomic radius of Be is smaller than Li but larger than H or He. We could continue this way, empirically measuring ionization energies for each element (see figure), but how do we make sense of the pattern observed, with its irregular repeating character that implies complications to a simple model of atomic structure?

2.7 Quantum Numbers^[17]

Quantum numbers (whose derivation we will not consider here) provide the answer to our dilemma. Basically we can describe the wave function for each individual electron in an atom by a distinct set of three quantum numbers, known as n, l, and ml. The principal quantum number, n, is a non-zero positive integer (n = 1, 2, 3, 4, etc.). These are often referred to as electron shells or orbitals, even though they are not very shell- or orbital-like. The higher the value of n, the higher the overall energy level of the electron shell. For each value of n there are only certain allowable values of l, and for each value of l, only certain allowable values of ml. Table 2.1 (next page) shows the allowable values of l and ml for each value of n are shown. There are a few generalizations we can make. Three quantum numbers, n, l, and ml, describe each orbital in an atom and each orbital can contain a maximum of two electrons. As they are typically drawn, each orbital defines the space in which the probability of finding an electron is 90%. Because each electron is described by a unique set of quantum numbers, the two electrons within a particular orbital must be different in some way.^[18] But because they are in the same orbital they must have the same energy and the same probability distribution. So what property is different? This property is called spin. The spin quantum number, ms, can have values of either + ½ or – ½.   Spin is responsible for a number of properties of matter including magnetism.

Hydrogen has one electron in a 1s orbital and we write its electron configuration as 1s¹.  Helium has both of its electrons in the 1s orbital (1s²). In lithium, the electron configuration is 1s2 2s¹, which tells us that during ionization, an electron is being removed from a 2s orbital. Quantum mechanical calculations tell us that in 2s orbital there is a higher probability of finding electrons farther out from the nucleus than the 1s orbital, so we might well predict that it takes less energy to remove an electron from a 2s orbital (found in Li) than from a 1s orbital (found in H). Moreover, the two 1s electrons act as a sort of shield between the nucleus and the 2s electrons. The 2s electrons feel what is called the effective nuclear charge, which is smaller than the real charge because of shielding by the 1s electrons. In essence, two of the three protons in the lithium nucleus are counterbalanced by the two 1s electrons. The effective nuclear charge in lithium is +1. The theoretical calculations are borne out by the experimental evidence—always a good test of a theory.

Table 2.1 Elemental electron shell organization

	s (l = 0)	p (l = 1)			d (l = 2)
	m = 0	m = 0	m = ±1		m = 0	m = ±1		m = ±2
	s	pz	px	py	[latex]d_{z^2}[/latex]	dxz	dyz	dxy	[latex]d_{x^2-y^2}[/latex]
n = 1
n = 2
n = 3

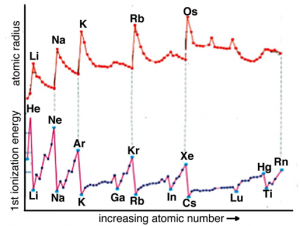
At this point, you might start getting cocky; you may even be ready to predict that ionization energies across the periodic table from lithium to neon (Ne) will increase, with a concomitant decrease in atomic radius. In the case of atomic radius, this is exactly what we see in the figure – as you go across any row in the periodic table the atomic radius decreases. Again, the reason for both these trends is that same: that is, each electron is attracted by an increasing number of protons as you go from Li to Ne, which is to say that the effective nuclear charge is increasing. Electrons that are in the same electron shell do not interact much and each electron is attracted by all the unshielded charge on the nucleus. By the time we get to fluorine (F), which has an effective nuclear charge of 9 – 2 = +7, and neon (10 – 2 = +8), each of the electrons are very strongly attracted to the nucleus, and very difficult to dislodge. Meaning that the size of the atom gets smaller, and the ionization energy gets larger^[19]

As you have undoubtedly noted from considering the graph, the increase in ionization energy from lithium to neon is not uniform: there is a drop in ionization energy from beryllium to boron and from nitrogen to oxygen. This arises from the fact that as the number of electrons in an atom increases the situation becomes increasingly complicated. Electrons in the various orbitals influence one another and some of these effects are quite complex and chemically significant. We will return to this in a little more detail in Chapter 3 and at various points through the rest of the book.

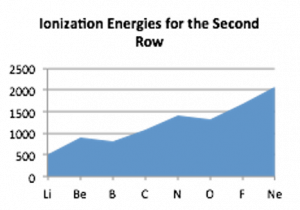If we use the ideas of orbital organization of electrons, we can make some sense of patterns observed in ionization energies. Let us go back to the electron configuration. Beryllium (Be) is 1s² 2s² whereas Boron (B) is 1s² 2s² 2p¹. When electrons are removed from Be and B they are removed from the same quantum shell (n = 2) but, in the case of Be, one is removed from the 2s orbital whereas in B, the electron is removed from a 2p orbital. s orbitals are spherically symmetric, p orbitals have a dumbbell shape and a distinct orientation. Electrons in a 2p orbital have lower ionization energies because they are on average a little further from the nucleus and so a little more easily removed compared to 2s electrons. That said, the overall average atomic radius of boron is smaller than beryllium, because on average all its electrons spend more time closer to the nucleus.

The slight drop in ionization potential between nitrogen and oxygen has a different explanation. The electron configuration of nitrogen is typically written as 1s² 2s² 2p³, but this is misleading: it might be better written as 1s² 2s² 2px¹ 2py¹ 2pz¹, with each 2p electron located in a separate p orbital. These p orbitals have the same energy but are oriented at right angles (orthogonally) to one another. This captures another general principle: electrons do not pair up into an orbital until they have to do so.^[20] Because the p orbitals are all of equal energy, each of them can hold one electron before pairing is necessary. When electrons occupy the same orbital there is a slight repulsive and destabilizing interaction; when multiple orbitals of the same energy are available, the lowest energy state is the one with a single electron in an orbital. Nitrogen has all three 2p orbitals singly occupied and therefore the next electron, which corresponds to oxygen, has to pair up in one of the p orbitals. Thus it is slightly easier to remove a single electron from oxygen than it is to remove a single electron from nitrogen, as measured by the ionization energy.

To pull together a set of seriously obscure ideas, the trends in ionization energies and atomic radii indicate that electrons are not uniformly distributed around an atom’s nucleus but rather have distinct distributions described by the rules of quantum mechanics. Although we derive the details of these rules from rather complex calculations and the wave behavior of electrons, we can cope with them through the use of quantum numbers and electron probability distributions. Typically electrons in unfilled shells are more easily removed or reorganized than those in filled shells because atoms with unfilled shells have higher effective nuclear charges. Once the shell is filled, the set of orbitals acts like a shield and cancels out an equal amount of nuclear charge. The next electron goes into a new quantum shell and the cycle begins again. This has profound implications for how these atoms react with one another to form new materials because, as we will see, chemical reactions involve those electrons that are energetically accessible: the valence electrons.

We could spend the rest of this book (and probably one or two more) discussing how electrons are arranged in atoms but in fact your average chemist is not much concerned with atoms as entities in themselves. As we have said before, naked atoms are not at all common. What is common is combinations of atoms linked together to form molecules. From a chemist’s perspective, we need to understand how, when, and where atoms interact. The electrons within inner and filled quantum shells are “relatively inert” which can be translated into English to mean that it takes quite a lot of energy (from the outside world) to move them around. Chemists often refer to these electrons as core electrons, which generally play no part in chemical reactions; we really do not need to think about them much more except to remember that they form a shield between the nucleus and the outer electrons. The results of their shielding does, however, have effects on the strong interactions, commonly known as bonds, between atoms of different types, which we will discuss in Chapters 4 and 5. Reflecting back on Chapter 1, we can think about the distinction between the London Dispersion Forces acting between He atoms and between H₂ molecules versus the bonds between the two H atoms in a H₂ molecule.

Bonds between atoms involve the valence electrons found in outer, and usually partially filled, orbitals. Because of the repeating nature of electron orbitals, it turns out that there are patterns in the nature of interactions atoms make—a fact that underlies the organization of elements in the periodic table. We will come back to the periodic table once we have considered how atomic electronic structure influences the chemical properties of the different elements.