12 Homogeneous Rates of Return
Lindon Robison
Learning goals. After completing this chapter, you should be able to (1) construct present value (PV) models using multi-period equivalents of accrual income statements (AIS); (2) find multi-period before and after-tax internal rates of return (IRR) on assets and equity and relate these to before and after-tax return on assets (ROA) and equity (ROE) derived from AIS; (3) understand the importance of measuring rates of return on defending and challenging investments using homogeneous measures: equity or assets; and (4) solve practical investment problems using PV model templates are consistent with generalized AIS construction principles.
Learning objectives. To achieve your learning goals, you should complete the following objectives:
- Describe the similarities and differences between an AIS and IRR PV models.
- Construct multi-period IRR models by generalizing AIS earning measures.
- Demonstrate that before and after-tax return on assets (ROA) and return on equity (ROE) measures derived from an AIS are equivalent (equal) to rate of return measures derived from multi-period (one-period) IRR models.
- Construct net present value (NPV) models by discounting a challenger’s cash flow using a defender’s IRR.
- Show how NPV models that discount a challenger’s cash flow and changes in operating and capital accounts with a defender’s IRR can be used to rank defenders and challengers.
- Learn how to construct PV models that measure returns on assets versus returns on equity and use homogeneous rates of return when comparing the profitability of investments.
- Develop PV construction skills by using Excel templates.
Introduction
This chapter demonstrates that present value (PV) models are multi-period generalizations of an accrual income statement (AIS). While the AIS and PV approaches each focus on changes in wealth, a major distinction involves the time value of money that is explicitly considered through discount rates in the multi-period PV analysis. We find it important for investment evaluations to identify the connections between these financial perspectives and their effects on alternative rates of return. In addition, we compare ROA and ROE derived in AIS to internal rates of return on assets, IRRA, and equity, IRRE. We note that returns on assets and equity may provide inconsistent rankings, making it all the more important that we use homogeneous rates of return when ranking investments.
We often describe PV models as a beginning investment and the discounted present value of cash flow and the liquidated value of the investment at the end of the analysis. In fact, most investments are much more complicated. For one thing, we need to determine if we are investigating returns on equity or assets. We need to account for changes in accounts receivable, inventories, accounts payable, and accrued liabilities. In sum, we need to be prepared to construct PV models with the same level of detail that is included in an AIS. Otherwise, we risk misrepresenting the investment (firm).
In what follows we show that before tax and after tax return on assets (ROA) and equity (ROE) derived from AIS equal one-period internal rates of return on assets (IRRA) and equity (IRRE). After recognizing the similarities between an AIS and one-period PV models, we generalize an AIS to construct multi-period PV models. Finally, we make the point that investment rankings based on IRRA and IRRE need not be consistent.
Finding Rates of Return on Assets (ROA) and Equity (ROE) from Accrual Income Statements (AIS)
Finding rates of return. Reduced to their essence, AIS measure rates of return as changes in beginning assets and equity. AIS report these changes as:
- changes in the cash balances during the period(s) of analysis,
- changes in the firm’s noncash operating and capital accounts that produce cash flow; and
- changes in the value of operating and capital accounts between the beginning and ending periods of analysis.
A numerical example. We now describe how to find rates of return using an AIS. To illustrate the process, we use Robison, Hanson, and Black’s (RHB, 2019) AIS for the fictional firm Hi-Quality Nursery (HQN) that we report in Table 12.1.
Table 12.1. 2018 Accrual Income Statement for HQN.
Open HQN Coordinated Financial Statement in MS Excel
| ACCRUAL INCOME STATEMENT |
||
| DATE | 2018 | |
| + | Cash Receipts | $38,990 |
| + | Change in Accounts Receivable | ($400) |
| + | Change in Inventories | $1,450 |
| + | Realized Cap. Gains/Depr. Recapture | $0 |
| Total Revenue | $40,000 | |
| + | Cash Cost of Goods Sold | $27,000 |
| + | Change in Accounts. Payable | $1,000 |
| + | Cash Overhead Expenses | $11,078 |
| + | Change in Accrued Liabilities | ($78) |
| + | Depreciation | $350 |
| Total Expenses | $39,350 | |
| Earnings Before Interest and Taxes (EBIT) | $650 | |
| – | Less Interests Costs | $480 |
| Earnings Before Taxes (EBT) | $170 | |
| – | Less Taxes | $68 |
| Net Income After Taxes (NIAT) | $102 | |
| – | Less Dividends and Owner Draw | $287 |
| Addition to Retained Earnings | ($185) | |
The AIS reported in Table 12.1 organizes cash flow and changes in operating and capital accounts into total revenue and total expenses. Then, after adjusting for interest, taxes, and dividend/owner draw, it finds HQN’s Addition to Retained Earnings.
Total revenue and expenses. Equation (12.1) summarizes the AIS statement. Total revenue equals cash receipts (CR), plus changes in accounts receivable (ΔAR), plus changes in inventory (ΔInv), plus realized capital gains (losses) (RCG). Total expenses equals cash cost of goods sold (COGS), plus the change in accounts payable (ΔAP), plus cash overhead expenses (OE), plus the change in accrued liabilities (ΔAL), plus the changes in the book value of capital assets or depreciation (Dep). HQN’s earnings before interest and taxes (EBIT) equals the difference between total revenue and total expenses.
(12.1) 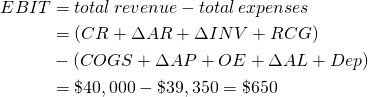
We find HQN’s rate of return on its assets, ROA, by dividing its EBIT by its beginning assets (A0). HQN’s beginning assets are equal to $10,000 as shown in Table 12.2.
(12.2) ![]()
Table 12.2. Beginning and Ending Balance Sheets for HQN (all numbers in 000s)
Open HQN Coordinated Financial Statement in MS Excel
| BALANCE SHEET | ||
| DATE | 12/31/2017 | 12/31/2018 |
| Cash and Marketable Securities | $930 | $600 |
| Accounts Receivable | $1,640 | $1,200 |
| Inventory | $3,750 | $5,200 |
| Notes Receivable | $0 | $0 |
| Total Current Assets | $6,320 | $7,000 |
| Depreciable Assets | $2,990 | $2,710 |
| Non-depreciable Assets | $690 | $690 |
| Total Long-Term Assets | $3,680 | $2,400 |
| TOTAL ASSETS | $10,000 | $10,400 |
| Notes Payable | $1,500 | $1,270 |
| Current Portion Long-Term Debt | $500 | $450 |
| Accounts Payable | $3,000 | $4,000 |
| Accrued Liabilities | $958 | $880 |
| Total current Liabilities | $5,958 | $6,600 |
| Non-Current Long Term Debt | $2,042 | $1,985 |
| TOTAL LIABILITIES | $8,000 | $8,585 |
| Contributed Capital | $1,900 | $1,900 |
| Retained Earnings | $100 | ($85) |
| Total Equity | $2,000 | $1,815 |
| TOTAL LIABILITIES AND EQUITY | $10,000 | $10,400 |
We find HQN’s ROE by subtracting from EBIT interest costs (Int) that represent returns on debt. We refer to the result as earnings before taxes (EBT). Dividing EBT by the firm’s beginning equity E0 reported in Table 12.2 as $2,000 we find ROE to equal:
(12.3) ![]()
Changes in beginning assets and equity versus changes between beginning and ending assets and equity. EBIT and EBT estimate changes in the firm’s beginning assets and equity. However, these estimates may not equal the changes in assets and equity between periods. To illustrate, in Table 12.2, the change in equity between periods equals $1815 – $2,000 = ($185) compared to an EBT of $170 estimated from its AIS. The difference between the change in beginning equity and change in equity between periods results from taxes of $68 and owner draw of $287. If we subtract these from EBT, we find the change in equity between periods of ($185).
(12.4) ![]()
Table 12.3 reports a change in HQN’s assets of $400 ($10,400 – $10,000). Meanwhile HQN’s AIS reports a change in HQN’s beginning assets, EBIT, of $650. We can explain part of the difference between EBIT and actual change in assets by accounting for interest and taxes paid and owner draw. These describe how operating activity change beginning and ending assets. hen if we add the effect of increased liabilities of $585 ($8585 – $8000), we can explain the discrepancy. We summarize these results in the Table 12.3.
Table 12.3. Reconciling the Change in HQN’s Assets versus Change in Beginning Assets Measured by EBIT
| EBIT | $650 | |
| – | Interest Paid | $480 |
| – | Taxes paid | $68 |
| – | Owner draw | $287 |
| = | Change in retained earnings | ($185) |
| + | Changes in total liabilities | $585 |
| = | Changes in total assets | $400 |
The main point is that while rates of return on assets and equity reflect some changes in beginning assets and equity, they do not necessarily equal the total difference between beginning and ending assets and equity. Therefore, we cannot measure rates of return on assets and equity as the changes in ending and beginning assets and equity.
Finding Internal Rates of Return on Assets (IRRA) and Equity (IRRE)
Reorganizing AIS data entries. We can reorganize AIS data into cash flow and changes in operating and capital accounts to build an IRR model that is appropriate for analyzing multi-period return on assets and equity. In an AIS, cash flow and changes in operating and capital accounts that produce cash flow occur in the same period. In PV models, cash flow and changes in accounts that produce cash flow can occur in multiple periods. Meanwhile we value the change in operating and capital accounts at the end of the analysis that may be after multiple periods as either book value or liquidation value. Separating AIS entries into cash flow and changes in operating and capital accounts produces Tables 12.4 and 12.5.
Table 12.4. HQN 2018 Cash Flow (Cash Receipts minus Cash Expenses)
| Cash Receipts (CR) | ||
| + | Cash receipts from operations | $38,990 |
| + | Realized capital gains | $0 |
| = | Cash Receipts (CR) | $38,990 |
| Cash Expenses (CE) | ||
| + | Cash COGS | $27,000 |
| + | Cash OE | $11,078 |
| = | Cash Expenses (CE) | $38,078 |
| Cash Receipts – Cash Expenses = CR – CE | $912 | |
Table 12.4 divides cash flow into cash receipts (CR) and cash expenses (CE). The sources of CR include cash sales from operations, reductions in accounts receivable (∆AR < 0), reductions in inventories held for sale (∆Inv < 0), and realized capital gains (RCG). The sources of cash expenses include COGS, OE, reductions in accounts payable (∆AP < 0), and reductions in accrued liabilities (∆AL < 0).
We record changes in operating and capital accounts in Table 12.5. Changes in operating asset accounts include changes include ∆AR and ∆Inv. Changes in operating liability accounts include ∆AP and ∆OE. Note that we include in CR and CE negative changes in operating accounts that produce cash flow. We include changes in operating accounts regardless of their sign in Table 12.5. Changes in the book value of capital assets, depreciation, are also included in Table 12.5.
Table 12.5. HQN 2018 Changes in operating accounts and depreciation
| + | Change in accounts receivable (∆AR) | ($440) |
| + | Change in inventories (∆Inv) | $1450 |
| – | Change in accounts payable (∆AP) | $1,000 |
| – | Change in accrued liabilities (∆AL) | ($78) |
| = | Changes in operating accounts | $88 |
| – | Depreciation (Dep) | $350 |
| = | Changes in capital accounts | $350 |
| = | Changes in operating and capital accounts | ($262) |
To summarize the calculations included in Tables 12.4 and 12.5 we express EBIT as the sum of cash flow and changes in operating and capital accounts:
(12.5) ![]()
Notice that the sum of cash flow recorded in Table 12.4 of $912 plus changes in operating accounts (∆AR + ∆INV – ∆AP – ∆AL – Dep) recorded in Table 12.5 of ($262) equal EBIT of $650, an amount equal to the difference in total revenue and total expenses recorded in equation (12.1).
Including beginning and ending value of accounts. When we found rates of return on assets and equity from an AIS, we divided EBIT and EBT by beginning assets and equity respectively. When we build PV models, we must account for the beginning value of assets and equity as well as relevant changes in their ending values, including only those changes that affect EBIT or EBT. We are not interested in explaining total changes in equity and assets over the periods of analysis, only those changes we can attribute to operating and investing activities. To that end, we rearrange equation (12.2):
(12.6) ![]()
Now suppose that we add A0 to both sides of equation (12.6) and, after factoring, divide both sides of equation (12.6) by (1 + ROA) to obtain:
(12.7) 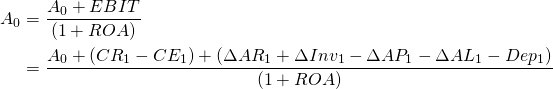
We can simplify equation (12.7). To do so, we substitute for A0, the value of capital assets V0 plus the value of current asset accounts Accts0 equal to AR0 and Inv0 plus beginning cash balance Csh0. The value of capital assets V0 less depreciation, Dep1, equals the book value of capital assets V1book at the end of the period. However, if the capital assets are actually liquidated, then the liquidation value can be written V1liquidation = V1book + RCG. Furthermore, Accts0 + (Accts1 ‒ Accts0) = Accts1, and Csh0 + (CR1 ‒ CE1) = Csh1. Now we can rewrite equation (12.7) as:
(12.8) 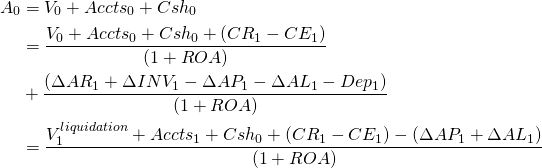
To write the multi-period equivalent of equation (12.8), we generalize our time subscripts t = 1, …, n. To convert cash flow and liquidated values of noncash operating and capital accounts to their present value we discount them using (1 + ROA). However, the discount rate in the multi-period equation is not the ROA derived from the one-period AIS but a multi-period average internal rate of return on assets (IRRA) that we substitute for ROA. We summarize our results in equation (12.9):
(12.9) 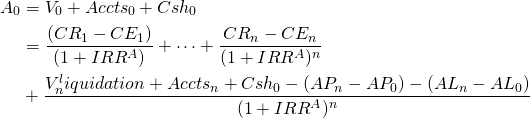
To demonstrate equation (12.9) with data from HQN, we set n = 1 and write:
(12.10) 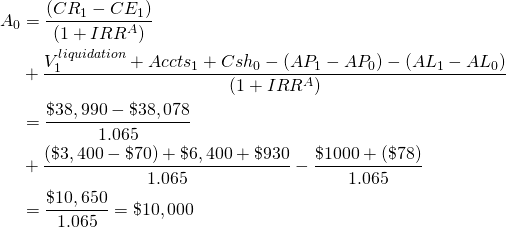
To explain equation (12.10), we compare the result with HQN’s AIS. We observe CR less CE (COGS + OE) produces $38,990 ‒ $38,078 = $912 (see Table 12.1). Ending period long-term assets (LTA) equal $3,400 (see Table 12.2) from which we subtract purchases minus sales of LTA ($100 ‒ $30 = $70). Ending account balances (Accts1 = AR1 + Inv1) equal $6400, and the beginning cash balance is $930. Next, we subtract changes in liability accounts because, as we pointed out earlier, increases in AP and AL increase ending cash balances in the balance sheet and reduce EBIT (See Table 12.3). Furthermore, because of taxes, the increase in assets is not equal to the reduction in EBIT.
EBT and ROE. We compute ROA by dividing returns from assets, EBIT, by beginning assets. We compute ROE by subtracting from beginning asset earnings interest paid for the use of debt all divided by beginning equity. To find the multi-period IRR for equity, IRRE, we subtract in each period t interest cost iDt–1 where Dt–1 equals the firm’s debt at the end of the previous period and i equals the average cost of debt. To find the amount of equity invested, we subtract from initial assets initial debt D0. Outstanding debt during the period of analysis collects interest. No changes in debt occur in the last period and debt at the end of the period n–1, Dn–1, is retired in the last period. Revising equation (12.10) to account for interest costs and debt and replacing ROE with the multi-period equivalent of ROE, IRRE, we can write:
(12.11) 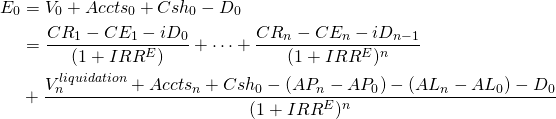
To illustrate equation (12.11) with data from HQN, we set n = 1 and write:
(12.12) 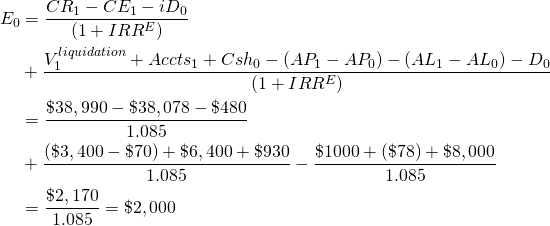
The explanations for equations (12.10) and (12.12) are the same except that in equation (12.12) we subtract interest charges ($480) from cash flow and total liabilities ($8,000) from beginning assets.
After-tax ROA and ROE Measures
PV models mostly use after-tax cash flow (ATCF). They focus on ATCF because it represents what the firm/investors keep after paying all their expenses including taxes. In what follows we present tax obligations in a simplified form to illustrate their impact on after tax rate of return. Our goal is to find the average tax rate T that adjusts ROE to ROE(1–T) and T* that adjusts ROA to ROA(1–T*). We do not try to duplicate the complicated processes followed by taxing authorities to find T and T*. Instead, we suggest that the firm pays an average tax rate T or T* on EBT and EBIT respectively.
An AIS reports taxes paid by the firm and subtracts them from EBT to obtain net income after taxes (NIAT). We calculate interest costs by multiplying the average interest rate i times beginning period debt Dt–1 (iDt-1) and subtract them from earnings to reduce tax obligations. As a result, NIAT represents changes in equity after we have paid both interest and taxes. In 2018, HQN paid $68 in taxes. To find the average tax rate HQN paid on its changes in equity, we set taxes equal to the average tax rate T times EBT:
(12.13) ![]()
Solving for the average tax rate T HQN paid on its earnings we find:
(12.14) ![]()
Finally, we adjust ROE for taxes and find HQN’s after-tax ROE to be:
(12.15) ![]()
An AIS and After-tax ROA. An AIS computes taxes paid by the firm on its returns to equity but not on its returns to assets. An AIS records only one value for taxes paid and these estimates account for tax savings resulting from interest payments. As a result, we cannot use the average tax rate T calculated for taxes paid on equity earnings to adjust ROA for taxes. To find the average tax rate T* that adjusts ROA to ROA(1–T*), we calculate taxes “as if” there were no interest costs to reduce the average tax rate T*. We find ROA(1–T*) in equation (12.16) as:
(12.16) ![]()
Solving for T* we find:
(12.17) ![]()
Equation (12.17) emphasizes an important point, that adjusting ROE and ROA for taxes nearly always requires different average tax rates. The only time that T = T* is when interest costs are zero. In that particular case, we can easily demonstrate that T* = T since EBIT = EBT:
(12.18) ![]()
A note on discount rates and the weighted cost of capital (WCC). It is common in many finance texts to assume that the discount rate is an exogenous variable observed in the financial markets. In small firms, the focus of this book, we find the discount rate by finding ROA on the defending investment. We focus on the ROA because firms may have similar amounts of assets while having distinct debt levels and equity. We can derive the WCC from an identity reflected in AIS calculations.
(12.19) 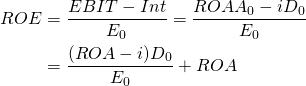
In equation (12.19) Int equals the average interest rate paid on debt i times beginning debt D0 and where beginning firm assets A0 equals the firm’s beginning debt D0 plus equity E0. Solving for ROA in equation (12.19) we find that ROA is a weighted average rate of return on equity ROE and the average cost of debt i. The weight applied to ROE is the percentage of beginning assets owned as equity. The weight applied to i is the percentage of beginning assets owed as debt.
(12.20) ![]()
We might ask: is there a multi-period equivalent of equation (12.20)? The answer is “sort of”. We could replace ROE with IRRE and ROA with IRRA. We are less confident about finding average weights applied to IRRE and i in equation (12.21).
(12.21) ![]()
We could also ask ourselves, since we can find IRRA why bother finding the WCC?
After-tax Multi-period IRRE Models
We are now prepared to introduce taxes into the IRRE model described in equation (12.11). We begin by solving for NIAT in equation (12.15) and replacing ROE(1 – T) with IRRE(1 – T):
(12.22) ![]()
Now we can write NIAT as:
(12.23) ![]()
Then, we substitute for EBIT the right-hand side of equation (12.5) and for NIAT, the right-hand side of equation (12.22):
(12.24)  \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-3216cf7229fe5125709940464d47be6a_l3.png)
Finally, we add we add E0 to both sides of equation (12.24) and after factoring [1 + IRRE (1 – T)] from the left hand side of (12.24) and divide both sides of equation (12.24) by the factor, we obtain:
(12.25) ![]()
Replacing E0 with Csh0 + Accts0 + V0 – D0 in the numerator of (12.25), we can write:
(12.26) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} E_0 & = \dfrac{Csh_0 + Accts_0 + V_0 - D_0}{[1 + IRR^E(1 - T)]} \\ & + \dfrac{ \Big[(CR_1 - CE_1 - Int_1) + (\Delta Accts_1 - \Delta AP_1 - \Delta AL_1 - Dep_1)\Big](1 - T)}{[1 + IRR^E(1 - T)]} \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-2a48b8e35021e61d4cb1e84ddcd649b9_l3.png)
Finally, we simplify equation (12.26) by recognizing that
- V0 – Dep1(1 – T) = V1book + TDep1,
- Int1 = iD0, and
- Accts0 + ∆Accts1(1 – T) = TAccts0 + (1 – T)Accts1
These simplifications allow us to rewrite equation (12.26) as:
(12.27) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} E_0 & = \dfrac{Csh_0 - D_0 + TAccts_0 + (1 - T)Accts_1 + V_1^{book} +TDep_1}{[1 + IRR^E(1 - T)]} \\ & + \dfrac{\Big[(CR_1 - CE_1 - iD_0) - (\Delta AP_1 + \Delta AL_1)\Big](1 - T)}{[1 + IRR^E(1 - T)]} \end{split}\end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-afb72903ef1460e9190115c967ecc760_l3.png)
To verify our results, we substitute HQN numerical values into equation (12.27) and find:
(12.28) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} E_0 & = \dfrac{\$930 - \$8,000 + \$2,156 + \$3,840 + \$3,330 + \$140 }{(1.051)} \\ & + \dfrac{\Big[(\$38,990 - \$38,078 - \$480) - (\$1,000 - \$78)\Big].6}{(1.051)} \\ & = \$2,000 \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-72f8d311b92209ecc7eda57a301eaf8c_l3.png)
To write the multi-period equivalent of equation (12.27) we discount n periods of operating income and in the nth period we liquidate operating and capital accounts.
(12.29) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} E_0 & = \dfrac{(CR_1 - CE_1 - iD_0)(1 - T) + TDep_1}{[1 + IRR^E(1- T)]} + \cdots \\ & + \dfrac{(CR_n - CE_n - iD_{n-1})(1 - T) + TDep_n}{[1 + IRR^E(1 - T)]^n} \\ & + \dfrac{Csh_0 - D_0 + TAccts_0 + (1 - T)Accts_n + V_n^{book}}{[1 + IRR^E(1 - T)]^n} \\ & - \dfrac{\Big[(AP_n - AP_0) + (AL_n - AL_0)\Big](1 - T)}{[1 + IRR^E(1 - T)]^n} \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-bf8576ae179c14fe0d11905bb71b2153_l3.png)
Capital gains (losses) and taxes. At the end of the analysis, PV models value their capital assets at their book value or if they indeed liquidate them, they value them for an amount equal to Vnliquidation. For tax purposes, if the difference between the liquidation and book value of capital assets is positive, (Vnliquidation – Vnbook) > 0, the firm or the investment has earned capital gains whose after-tax value is (1 – T)(Vnliquidation – Vnbook) > 0. On the other hand, if the difference is negative (Vnliquidation – Vnbook) < 0, then the firm has suffered a capital loss and earned tax credits whose after-tax value loss is (1 – T)(Vnliquidation – Vnbook) < 0. To simplify the tax discussion, we ignore the tax rate differences between income, capital gains, and depreciation recapture and apply only one tax rate T, the average of all tax rates. Finally, to adjust capital accounts for taxes, we replace Vnbook in equation (12.29) with what follows:
(12.30) ![]()
Now we can write the after-tax IRRE model for changes in equity consistent with principles followed when we constructed an AIS.
(12.31) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} E_0 & = \dfrac{(CR_1 - CE_1 - iD_0)(1 - T) + TDep_1}{[1 + IRR^E(1 - T)]} + \cdots \\ & + \dfrac{(CR_n - CE_n - iD_{n-1})(1 - T) + TDep_n}{[1 + IRR^E(1 - T)]^n} \\ & + \dfrac{Csh_0 - D_0 + TAccts_0 + (1 - T)Accts_n}{[1 + IRR^E(1 -T)]^n} \\ & + \dfrac{(1 - T)V_n^{liquidation} + TV_n^{book}}{[1 + IRR^E(1 -T)]^n} \\ & - \dfrac{\Big[(AP_n - AP_0 )+ (AL_n - AL_0)\Big](1 - T)}{[1 + IRR^E(1 -T)]^n} \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-686f6f04c79f210469e6e6eccdbb1502_l3.png)
After-tax Multi-period IRRA Model
There is a paradox in applied PV models. The paradox is that there is no explicit measure for T* that can be used to find ROA(1 – T*). This peculiar result occurs because taxes must account for interest costs that we do not consider when finding EBIT. Yet, many applied IRR models solve for after-tax return on assets that depend on ROA(1 – T*) calculations. An AIS provides such a measure allowing us to write:
(12.32) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} A_0 & = \dfrac{(CR_1 - CE_1)(1 - T^*) + T^*Dep_1}{[1 + IRR^A(1 - T^*)]} + \cdots \\ & + \dfrac{(CR_n - CE_n)(1 - T^*) + T^*Dep_n}{[1 + IRR^A(1 - T^*)]^n} \\ & + \dfrac{Csh_0 + T^*Accts_0 + (1 - T^*)Accts_n}{[1 + IRR^A(1 -T^*)]^n} \\ & + \dfrac{(1 - T^*)V_n^{liquidation} + T^*V_n^{book}}{[1 + IRR^A(1 -T^*)]^n} \\ & - \dfrac{\Big[(AP_n - AP_0 )+ (AL_n - AL_0)\Big](1 - T^*)}{[1 + IRR^A(1 -T^*)]^n} \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-29b5a3ee506527f1abcbe715e44a13cc_l3.png)
The main difference between equations (12.31) and (12.32) is that T is replaced with T*, interest charges are not subtracted from periodic cash flow, and initial liabilities are no longer subtracted. All these changes are required so that earnings can be attributed to beginning assets rather than beginning equity.
Although there is no explicit AIS measure corresponding to equation (12.32), we do know the value of beginning assets A0 and IRRA(1 – T* ) so we can write the one period HQN numerical equivalent of (12.32) assuming capital assets are valued at their book value:
(12.33) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} A_0 & = \dfrac{Csh_0 + T^*Accts_0 + (1 - T^*)Accts_1 + V_1^{book} + T^*Dep_1}{[1 + IRR^A(1 - T^*)]} \\ & + \dfrac{\Big[(CR_1 - CE_1) - (\Delta AP_1 + \Delta AL_1)\Big](1 - T^*)}{[1 + IRR^A(1 - T^*)]} \\ & = \dfrac{\$930 + \$565.95 + \$5,728 + \$3,330 + \$36.75}{(1.058)} \\ & + \dfrac{\Big[(\$38,990 - \$38,078) - ( \$1,000 - \$78)\Big].895}{(1.058)} \\ & = \$10,000 \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-78311941d0d3efd7aa1f120684960025_l3.png)
A Generalized Template
This section operationalizes the concepts presented in this chapter by presenting a generalized PV template corresponding to AIS estimated value of NIAT—after-tax return on equity described in equation (12.31). To facilitate the generalization of equation (12.31) and the corresponding template we replace beginning equity E0 with beginning assets A0 minus beginning liabilities D0. Then we convert (12.31) to an NPV equation by discounting the challenger’s cash flows with the defender’s IRRE and by subtracting equity from both sides. We rewrite (12.31) as an NPV equation equal to:
(12.34) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} NPV & = - (A_0 - D_0) \\ & + \dfrac{(CR_1 - CE_1 - id_0)(1 - T) + TDep_1}{[1 + IRR^E(1 - T)]} + \cdots \\ & + \dfrac{(CR_n - CE_n - iD_{n - 1})(1 - T) + TDep_n}{[1 + IRR^E(1 - T)]^n} \\ & + \dfrac{(Csh_0 - D_0 + TAccts_0 + (1 - T)Accts_n}{[1 + IRR^E(1 -T)]^n} \\ & + \dfrac{(1 - T)V_n^{liquidation} + TV_n^{book}}{[1 + IRR^E(1 -T)]^n} \\ & - \dfrac{\Big[(AP_n - AP_0 )+ (AL_n - AL_0)\Big](1 - T)}{[1 + IRR^E(1 -T)]^n} \end{split} \end{equation*}](https://openbooks.lib.msu.edu/app/uploads/quicklatex/quicklatex.com-d03a07307aed5dca5c6f02b5f92b1140_l3.png)
Now we introduce the general NPV template as:
Table 12.6. A Generalized PV Model Template with Rolling NPV and AE Estimates Corresponding to NIAT Measures from AIS.
Open Table 12.6 in Microsoft Excel
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | |
| 3 | Yr | Assets | Debt capital | Capital accounts liquidation value | Capital accounts book value | Asset Operating accounts (AR + INV ) | Liability Operating Accounts (AP+AL) | Capital accts. depr. | Tax svg. from depr. | Cash Receipts (CR) | Cash Cost of Goods Sold (COGS) | Cash Overhead Expenses (OEs) | Interest costs | ATCF from operations | ATCF from liquidating asset accounts | ATCF from liquidating liability accounts | After-tax capital gains | ATCF from liquidations/ depr. | Rolling NPV |
Rolling AE |
| 4 | 0 | $10,000.00 | $8,000.00 | $3,680.00 | $5,390.00 | $3,958.00 | ||||||||||||||
| 5 | 1 | $0.00 | $8,000.00 | $3,330.00 | $3,330.00 | $6,400.00 | $4,880.00 | $350.00 | $140.00 | $38,990.00 | $27,000.00 | $11,078.00 | $480.00 | $399.20 | $606.00 | $553.20 | $0.00 | $1,702.80 | $0.00 | $0.00 |
| 6 | 2 | $0.00 | $8,080.00 | $3,263.40 | $2,997.00 | $6,464.00 | $4,928.80 | $333.00 | $133.20 | $39,379.90 | $27,270.00 | $11,188.78 | $480.00 | $397.87 | $1,019.23 | $582.48 | $159.84 | $2,263.59 | $789.26 | $425.07 |
| 7 | 3 | $0.00 | $8,160.80 | $3,198.13 | $2,697.30 | $6,528.64 | $4,978.09 | $299.70 | $119.88 | $39,773.70 | $27,542.70 | $11,300.67 | $484.80 | $387.20 | $1,070.32 | $612.05 | $300.50 | $2,459.07 | $1,191.72 | $438.43 |
| 8 | 4 | $0.00 | $8,242.41 | $3,134.17 | $2,427.57 | $6,593.93 | $5,027.87 | $269.73 | $107.89 | $40,171.44 | $27,818.13 | $11,413.67 | $489.65 | $377.88 | $1,191.89 | $641.92 | $423.96 | $2,704.20 | $1,599.54 | $452.14 |
| 9 | 5 | $0.00 | $8,324.83 | $3,071.49 | $2,184.81 | $6,659.87 | $5,078.15 | $242.76 | $97.10 | $40,573.15 | $28,096.31 | $11,527.81 | $494.54 | $369.79 | $1,295.26 | $672.09 | $532.00 | $2,912.42 | $1,942.74 | $449.97 |
The column headings in Table 12.6 describe exogenous and endogenous variables used to find rolling (every year) NPV and AE estimates and correspond to variables in equation (12.34). Highlighted data in Table 12.6 in lines 4 and 5 are exogenous values obtained from HQN’s coordinated financial statements. Table cells that are not highlighted are endogenous or projected values. Projecting values is a subject to which we will return in Chapter 13. Now we describe in more detail the values in Table 12.6 and their correspondence to equation (12.34).
- Column A lists the periods t at the end of which financial activity occurs and values are recorded.
- Columns B line 4 lists total investment amount A0 including beginning cash Csh0, beginning accounts receivable and inventories (AR0 + Inv0), plus capital investments V0
- Column C line 4 lists D0 beginning current liabilities and noncurrent long-term liabilities supporting the firm’s assets on which interest is paid. Subsequent values in Column C list the amount of outstanding liabilities in each period.
- Column D lists the liquidation value of capital investments. Since Table 12.6 calculates rolling estimates of NPV and AE, we are required to estimate the liquidated value of the investment in each period.
- Column E lists the book value of capital investments determined by the initial purchase price and depreciation amounts made available by taxing authorities and selected by financial managers.
- Column F lists the value of accounts receivable ARt and inventory Invt at the end of each period t.
- Column G lists the value of accounts payable APt and accrued liabilities ALt at the end of each period t.
- Column H calculates depreciation equal to the change in the investment’s book value.
- Column I calculates tax savings from depreciation by multiplying capital asset depreciation by the average tax rate.
- Column J reports cash receipts in period t, CRt, equal to the sum of cash sales plus negative changes in ARt and Invt.
- Column K reports cash cost of goods sold in period t, COGSt, equal to cash operating expenses plus reductions in APt.
- Column L reports cash overhead expenses in period t, OEt, equal to cash overhead expenses plus reductions in ALt.
- Column M calculates interest costs iDt–1 by multiplying periodic liabilities at the end of the previous period Dt–1 by the average interest rate i.
- Column N calculates after-tax cash flow from operations in period t, (ATCFt) equal to (CRt – COGSt – OEt – iDt–1)(1 – T) + TDept–1.
- Column O calculates cash flow from after-tax liquidation of accounts receivable and inventories (1 – T)(ARn + Invn) plus a tax adjustment coefficient T(AR0 + Inv0) because beginning accounts receivable and inventories have already been taxed.
- Column P calculates cash flow from after-tax liquidation of changes in liability operating accounts (APn – AP0 + ALn – AL0)(1 – T).
- Column Q calculates the cash flow from after-tax liquidation of capital gains (1 – T)(Vnliquidation – Vnbook).
- Column R sums liquidated cash flow calculated in columns (O – P + Q – H) plus (A0 – D0) together which can be described as the numerator in the second fraction in equation 12.34.
- Column S calculates rolling NPV as though the investment ended in each year using Excel’s NPV function by finding the present value of ATCFt plus the liquidation value of the assets minus the initial equity invested in column R.
- Column T calculates rolling AE associated with the NPV for each year using Excel’s PMT function by finding the payment whose present value equals NPV for the corresponding period in column S.
Note that the sum of after-tax operating income of reported in column N of $399.20 plus the after-tax liquidation value of assets reported in column R of $1702.80 equals $2102 or the beginning equity of $2,000 plus NIAT of $102. Then discounting $2102 by HQN’s after-tax ROE of 5.1% and subtracting equity invested of $2,000, we find NPV equal to zero.
Adjusting the PV Model Template to Calculate Earnings and Rate of Return on Assets and Equity
We noted that the calculations in Table 12.6 corresponded to NIAT calculations in AIS models. We could likewise find calculations in Table 12.6 that corresponded to EBIT by setting all liability values in column C, interest rate i and tax rate T equal to zero and set the discount rate equal to 6.5%, the rate of return on assets (ROA). The result is Table 12.7.
Table 12.7. A Generalized PV Model Template with Rolling NPV and AE Estimates Corresponding to EBIT Measures from AIS.
Open Table 12.7 in Microsoft Excel
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | |
| 3 | Yr | Assets | Debt capital | Capital accounts liquidation value | Capital accounts book value | Asset Operating accounts (AR + INV ) | Liability Operating Accounts (AP+AL) | Capital accts. depr. | Tax svg. from depr. | Cash Receipts (CR) | Cash Cost of Goods Sold (COGS) | Cash Overhead Expenses (OEs) | Interest costs | ATCF from operations | ATCF from liquidating asset accounts | ATCF from liquidating liability accounts | After-tax capital gains | ATCF from liquidations/ depr. | Rolling NPV |
Rolling AE |
| 4 | 0 | $10,000 | $0.00 | $3,680.00 | $5,390.00 | $3,958.00 | ||||||||||||||
| 5 | 1 | $0.00 | $0.00 | $3,330.00 | $3,330.00 | $6,400.00 | $4,880.00 | $350.00 | $0.00 | $38,990.00 | $27,000.00 | $11,078.00 | $0.00 | $912.00 | $1,010.00 | $922.00 | $0.00 | $9,738.00 | $0.00 | $0.00 |
| 6 | 2 | $0.00 | $0.00 | $3,263.40 | $2,997.00 | $6,464.00 | $4,928.80 | $333.00 | $0.00 | $39,379.90 | $27,270.00 | $11,188.78 | $0.00 | $921.12 | $1,004.19 | $970.80 | $266.40 | $9,966.79 | $455.76 | $250.33 |
| 7 | 3 | $0.00 | $0.00 | $3,198.13 | $2,697.30 | $6,528.64 | $4,978.09 | $299.70 | $0.00 | $39,773.70 | $27,542.70 | $11,300.67 | $0.00 | $930.33 | $1,138.64 | $1,020.09 | $500.83 | $10,319.68 | $981.77 | $370.69 |
| 8 | 4 | $0.00 | $0.00 | $3,134.17 | $2,427.57 | $6,593.93 | $5,027.87 | $269.73 | $0.00 | $40,171.44 | $27,818.13 | $11,413.67 | $0.00 | $939.63 | $1,191.89 | $1,069.87 | $706.60 | $10,558.89 | $1,376.69 | $401.86 |
| 9 | 5 | $0.00 | $0.00 | $3,071.49 | $2,184.81 | $6,659.87 | $5,078.15 | $242.76 | $0.00 | $40,573.15 | $28,096.31 | $11,527.81 | $0.00 | $949.03 | $1,295.26 | $1,120.15 | $886.67 | $10,819.03 | $1,758.31 | $423.11 |
Note that the sum of after-tax operating income of reported in column N of $912.00 plus the after-tax liquidation value of assets reported in column R of $9,738 equal $10,650 or beginning equity of $10,000 plus EBIT of $650. Then discounting $10,650 by HQN’s before-tax ROA of 6.5% and subtracting beginning assets of $10,000 we find NPV equal to zero.
We can adjust the template to find earning values corresponding EBT by listing the value of liabilities in column C and listing the average interest costs i of 6%, the average rate earned by liabilities held by HQN. The result is Table 12.8.
Table 12.8. A Generalized PV Model Template with Rolling NPV and AE Estimates Corresponding EBT Measures from AIS.
Open Table 12.8 in Microsoft Excel
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | |
| 3 | Yr | Assets | Debt capital | Capital accounts liquidation value | Capital accounts book value | Asset Operating accounts (AR + INV ) | Liability Operating Accounts (AP+AL) | Capital accts. depr. | Tax svg. from depr. | Cash Receipts (CR) | Cash Cost of Goods Sold (COGS) | Cash Overhead Expenses (OEs) | Interest costs | ATCF from operations | ATCF from liquidating asset accounts | ATCF from liquidating liability accounts | After-tax capital gains | ATCF from liquidations/ depr. | Rolling NPV |
Rolling AE |
| 4 | 0 | $10,000 | $8,000 | $3,680 | $5,390 | $3,958 | ||||||||||||||
| 5 | 1 | $0 | $8,585 | $3,330 | $3,330 | $6,400 | $4,880 | $350 | $0 | $38,990.00 | $27,000 | $11,078 | $480 | $432.00 | $1,010.00 | $922.00 | $0.00 | $1,738.00 | $0.00 | $0.00 |
| 6 | 2 | $0 | $8,671 | $3,263 | $2,997 | $6,464 | $4,929 | $333 | $0 | $39,379.90 | $27,270 | $11,189 | $515 | $406.02 | $982.71 | $970.80 | $266.40 | $1,945.31 | $395.51 | $223.31 |
| 7 | 3 | $0 | $8,758 | $3,198 | $2,697 | $6,529 | $4,978 | $300 | $0 | $39,773.70 | $27,543 | $11,301 | $520 | $410.08 | $1,070.32 | $1,020.09 | $500.83 | $2,251.37 | $826.72 | $323.69 |
| 8 | 4 | $0 | $8,845 | $3,134 | $2,428 | $6,594 | $5,028 | $270 | $0 | $40,171.44 | $27,818 | $11,414 | $525 | $414.18 | $1,191.89 | $1,069.87 | $706.60 | $2,558.89 | $1,209.40 | $369.21 |
| 9 | 5 | $0 | $8,934 | $3,071 | $2,185 | $6,660 | $5,078 | $243 | $0 | $40,573.15 | $28,096 | $11,528 | $531 | $418.32 | $1,295.26 | $1,120.15 | $886.67 | $2,819.03 | $1,515.96 | $384.70 |
The calculations in Table 12.8 corresponded to EBT calculations in AIS models. We can find calculations in Table 12.8 that corresponded to EBT by setting beginning liability in column C equal to $8,000 and average interest rate i equal to 6% and set tax rate T equal to zero. Finally, we set the discount rate, the defender’s IRR equal to 8.5%, the rate of return on equity (ROE).
Note that the sum of after-tax operating income of reported in column N of $432.00 plus the after-tax liquidation value of assets reported in column R of $1,738 equal $10,650 or beginning equity of $2,000 plus EBIT of $170. Then discounting by $2,170 by HQN’s before-tax ROE of 8.5% and subtracting beginning equity of $2,000 we find NPV equal to zero.
In sum, by adjusting liabilities, interest costs, and tax rates, we can derive PV earning measures corresponding to NIAT, EBIT, and EBT measures calculated in AIS. This provides us an interesting interpretation of PV models. Discounting after-tax multi-period earnings on equity provides a measure corresponding the present value of future NIAT calculations. Discounting before-tax multi-period earnings on assets provides a measure corresponding the present value of future EBIT calculations. Finally, discounting before-tax multi-period earnings on equity provides a measure corresponding the present value of future EBT calculations.
Consistent Investment Rankings and Returns on Assets versus Equity
Suppose that we decided to rank two challengers using their IRRA and satisfied the homogeneity conditions described in Robison, Barry, and Myers (2015). There is no reason to expect that the IRRA rankings would equal the IRRE rankings because they represent different investment sizes. In the case of HQN, the initial asset investment of $10,000 does not equal the initial equity investment of $2,000.
We can construct PV models that find before-tax or after-tax returns on equity or assets and use them to rank investments. However, because they violate the homogeneity of initial and periodic size required for consistent rankings, we need not expect IRRA and IRRE nor IRRA(1 – T*) and IRRE(1 – T) to rank investments consistently. Nor can we even be sure that IRRA and IRRA(1 – T*) and IRRE and IRRE(1 – T) will rank investments consistently. One reason they need not be consistent is that their initial and periodic sizes are different. Interest costs alone included in the IRRE model and not in the IRRA model may produce investment ranking inconsistencies.
To make clear that IRRA and IRRE measures may produce different rankings, consider HQN’s one-period IRRA of 6.5% ($650/$10,000) and its one-period ROE of 8.5% ($170/$2,000) respectively. Let the original HQN asset and earning measures describe investment A. Now without changing beginning assets or equity, suppose a different investment B incurred no interest (or a different interest cost). Then investment B’s ROA would be unchanged ($650/$10,000); however, its ROE would increase to 32.5% ($650/$2,000). Meanwhile the investor would continue to be indifferent between investments A and B based on their IRRA (and NPV) since both equal 6.5%. However, clearly investment B is preferred to A based on their IRRE (and NPV). We learn the lesson that returns on assets and returns on equity may provide inconsistent investment rankings.
So, how do we decide on our ranking criterion? Do we focus on equity or asset earnings? Equity or asset earnings before or after paying taxes? Although there may not be any one satisfactory answer to this question, it surely must depend on, among other things, what questions the financial manager wants to answer.
Summary and Conclusions
We now make explicit the main point of this Chapter. PV models should be constructed as multi-period expressions of information found in an AIS. Furthermore, EBIT measures calculated in an AIS correspond to earnings from assets in PV models. EBT corresponds to earnings from equity in PV models, and NIAT corresponds to after-tax earnings from equity in PV models. While there is no explicit AIS measure of after-tax earnings from assets, it can be implied and easily measured.
Rates of return measures derived in AIS and IRR models are descriptive in nature—they describe a single investment. However, we can also use them prescriptively by comparing them with IRRs of other firms and investments. We can construct a prescriptive PV model, an NPV model, by discounting cash flow from a challenging investment using the IRR of a defending investment. (The challenging investment is one considered for a replacing to a defending investment already in use by the firm.) If the NPV is positive (negative), we recommend replacing (leaving in place) the defending investment.
There are other PV models besides IRR and NPV models. These include variants of NPV or IRR models. Maximum bid (minimum sell) models find the maximum bid (minimum sell) that can be paid (received) for a challenger and still earn the IRR of the defender. Loan formulae are special PV models that describe an amount to be paid to receive a challenging investment, a loan, while the defender earns its interest rate. Annuity equivalent models find a multi-period time adjusted average of a challenger’s cash flow. Replacement flows are special NPV models that find the optimal life of a repeatable investment that maximizes its NPV and the NPV of future replacements.
We conclude with the uncomfortable result that investment rankings based on asset earnings and equity earnings need not be consistent.
Questions
- List similarities and differences between an AIS statement and a PV model.
- Both AIS and PV models find rates of return on assets and equity using cash flow and changes in operating and capital asset accounts. However, they organize them differently. Explain how AIS and PV models organize cash flow and changes in operating and capital asset accounts differently.
- We can describe ROA and ROE as measures of changes in assets and equity respectively divided by original asset and equity values. Please explain.
- EBIT measures the change in the value of the firm’s assets before adjusting for taxes during a single period. Do you agree or disagree? Defend your answer.
- EBT measures the change in the value of the firm’s equity before adjust for taxes during a single period. Do you agree or disagree? Defend your answer.
- Measures the change in the value of the firm’s equity after adjusting for taxes during a single period. Do you agree or disagree? Defend your answer.
- There is no measure in an AIS statement that finds the change in assets after adjusting for taxes. Can you explain why?
- Use the template reported in Table 12.5 to find the change in assets after adjust for taxes. To find the after-tax change in assets, use an average tax rate of T*=10.46% and a discount rate of ROA(1 – T*) = (6.5%)(1 – 10.46%) = 5.8%.
- Describe the conditions under which NPV or IRR asset and equity models would rank challenging and defending investment consistently.
- Give an example in which NPV or IRR asset and equity models rank challenging and defending investments inconsistently.
- As a financial manager tasked with ranking a defending and a challenging investment, which ranking criteria would you employ: NPV earned by equity or NPV earned by assets? Defend your answer.

