6 Properties of matter
Saul Beceiro-Novo
Learning Objectives
- State the common phases of matter.
- Explain the physical characteristics of solids, liquids, and gases.
- Describe the arrangement of atoms in solids, liquids, and gases.
- Define density.
- Calculate the massof a reservoir using its density and volume.
- Compare and contrast the densities of various biological and physical substances.
- Define pressure.
- Explain the relationship between pressure and force.
- Calculate force given pressure and area.
- Define pressure in terms of the weight of a fluid.
- Explain how pressure varies with depth in a fluid.
- Calculate fluid density using pressure and depth or altitude data.
- State Pascal’s principle.
- Understand how Pascal’s principle applies to biological and medical systems.
- Derive relationships between forces in a hydraulic system.

Much of what we value in life is fluid: a breath of fresh winter air; the hot blue flame in our gas cooker; the water we drink, swim in, and bathe in; and the blood in our veins. What exactly is a fluid? Can we understand fluids using the physical laws we’ve already encountered, or do new principles emerge from their study?
This chapter explores the physical characteristics of static (stationary) fluids and the laws that govern their equilibrium.
Matter most commonly exists as a solid, liquid, or gas; these are the three common . Solids have a definite shape and volume. Liquids maintain a definite volume but take the shape of their container. Gases have neither definite shape nor volume and expand to fill their container. (Figure 75.1)
Liquids and gases are classified as because they yield to , unlike solids which resist such deformation. The extent to which fluids flow in response to these forces depends on a property called , which we’ll explore further in Viscosity and Laminar Flow; Poiseuille’s Law.
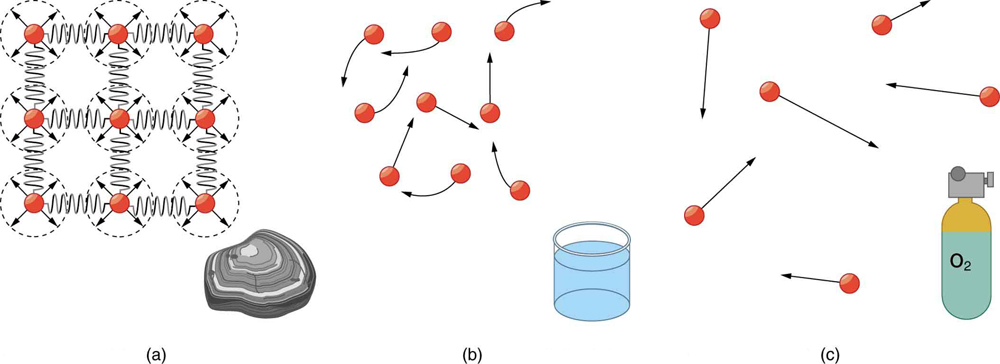
In solids, atoms are tightly packed in a regular structure. They vibrate but cannot easily move past one another. The forces between atoms act like stiff springs, resisting compression and shearing forces. This rigidity explains why solids maintain their shape and volume.
Connections: Submicroscopic Explanation of Solids and Liquids
The atomic and molecular structures of solids and liquids explain their macroscopic behaviors. This approach—linking submicroscopic structure to physical behavior—is a recurring theme in this course and is explored further in Conservation of Momentum.
By contrast, in liquids, atoms are still in close contact but are free to slide past one another. Liquids resist compression like solids, but they do not resist shearing forces and thus can flow. Liquids stay in an open container due to interatomic attraction, unless the container leaks.
In gases, atoms are spaced far apart and interact weakly. They move freely and rapidly, colliding with one another and the container walls. Because of the large spacing, gases are easily compressed and will escape from an open container. Both liquids and gases are considered fluids, but gases are distinct in being highly compressible.
Key Concept: Density
Which weighs more, a ton of feathers or a ton of bricks? This classic riddle draws attention to the difference between mass and density. Although both have the same mass (a ton), feathers take up much more space because their density is much lower than that of bricks. (See Figure 76.1.)
Density is a key physical property used in many scientific and clinical applications—for example, determining if an object floats in water, comparing the composition of tissues, or evaluating whether a substance will disperse or settle in a solution.
Density is defined as the mass per unit volume of a substance:
Here, [latex]\rho[/latex] (rho) is the density, [latex]m[/latex] is the mass, and [latex]V[/latex] is the volume. The SI unit of density is [latex]\text{kg/m}^3[/latex], although [latex]\text{g/cm}^3[/latex] or [latex]\text{g/mL}[/latex] are also commonly used in medicine and biology.
Density tells us how much mass is packed into a given volume. Substances with high density (like bone or lead) contain more matter per unit volume than low-density substances (like fat or air).
In the riddle, a ton of feathers takes up much more space than a ton of bricks because feathers have a low density. This volume difference is key in applications like lung imaging, blood analysis, or measuring body composition.
Table 76.1 shows the densities of various solids, liquids, and gases relevant to physics, biology, and environmental science. Note that gases have significantly lower densities than liquids or solids due to the greater spacing between their molecules.
Example 76.1: Calculating the Mass of a Reservoir
Problem: A reservoir has a surface area of [latex]50.0 \, \text{km}^2[/latex] and an average depth of [latex]40.0 \, \text{m}[/latex]. What is the total mass of water in the reservoir? (See Figure 76.2 for a view of a large reservoir—the Three Gorges Dam site on the Yangtze River in central China.)
Strategy
We use the formula for density:
The volume [latex]V[/latex] of the reservoir is calculated from its surface area [latex]A[/latex] and depth [latex]h[/latex]:
Using [latex]\rho = 1.00 \times 10^3 \, \text{kg/m}^3[/latex] for water, we find:
Discussion
The reservoir contains over 2 trillion kilograms of water. This mass plays a critical role in hydroelectric energy production, flood control, and ecological balance.

Take-Home Experiment: Sugar vs. Salt
Take equal volumes of sugar and salt. Which one is heavier? The difference in weight comes from their different densities and crystalline structures. Try measuring mass and volume to calculate density yourself!
You’ve likely encountered the concept of pressure in multiple contexts—for example, in discussions of blood pressure or atmospheric pressure. Pressure plays a vital role in physiology, medicine, and meteorology, among other fields. In physics, pressure is defined as the amount of force applied per unit area:
Here, [latex]F[/latex] is the magnitude of the applied force, and [latex]A[/latex] is the area over which the force is distributed, perpendicular to the surface.
Pressure is a scalar quantity that expresses how concentrated a force is when applied to a surface. Mathematically:
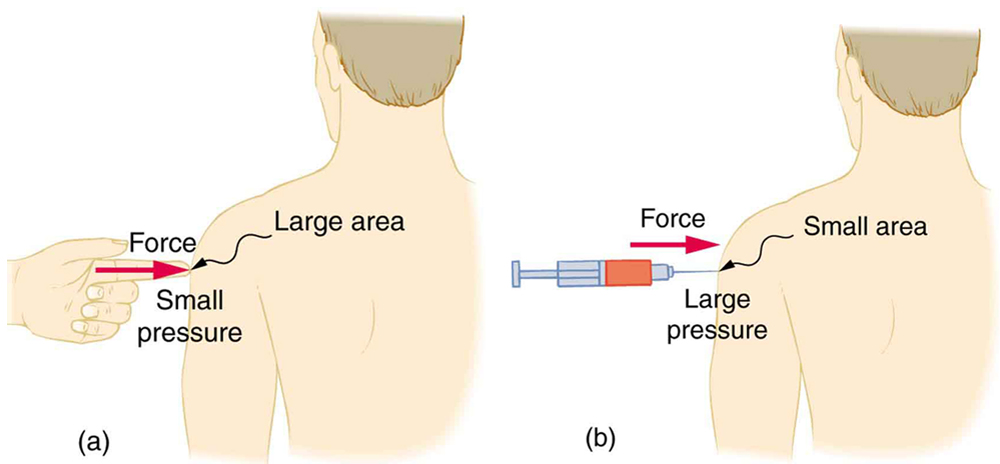
The same force can have very different effects depending on the contact area. For example, a gentle push with a finger spreads over a broad area, producing low pressure. In contrast, a needle tip applies the same force over a tiny area, creating high pressure that can pierce skin (see Figure 77.1).
The SI unit of pressure is the pascal (Pa):
Other common pressure units include:
- millibar (mb): used in meteorology; [latex]100~\text{mb} = 1 \times 10^5~\text{Pa}[/latex]
- pounds per square inch (psi): used in tire pressure and engineering
- millimeters of mercury (mm Hg): used in measuring blood pressure
Example 77.1: Calculating Force Exerted by Air
Problem: An astronaut is working outside the International Space Station, where atmospheric pressure is essentially zero. The pressure gauge on her air tank reads [latex]6.90 \times 10^6~\text{Pa}[/latex]. What force does this pressure exert on the flat end of the cylindrical tank, which is a disk 0.150 m in diameter?
Strategy
Use the formula [latex]F = PA[/latex] where area [latex]A = \pi r^2[/latex].
Solution
Discussion
This force is extremely large—over 122,000 newtons! That’s why pressurized tanks must be engineered to withstand such forces. The result also shows that pressure’s effect depends both on its magnitude and the area over which it acts.
Importantly, the force due to pressure in a fluid is always exerted perpendicular to the surface. This is because fluids cannot resist shearing (sideways) forces, so they can’t exert them either. Though pressure is a scalar, the forces it generates have well-defined directions—always perpendicular to surfaces (see Figure 77.2).
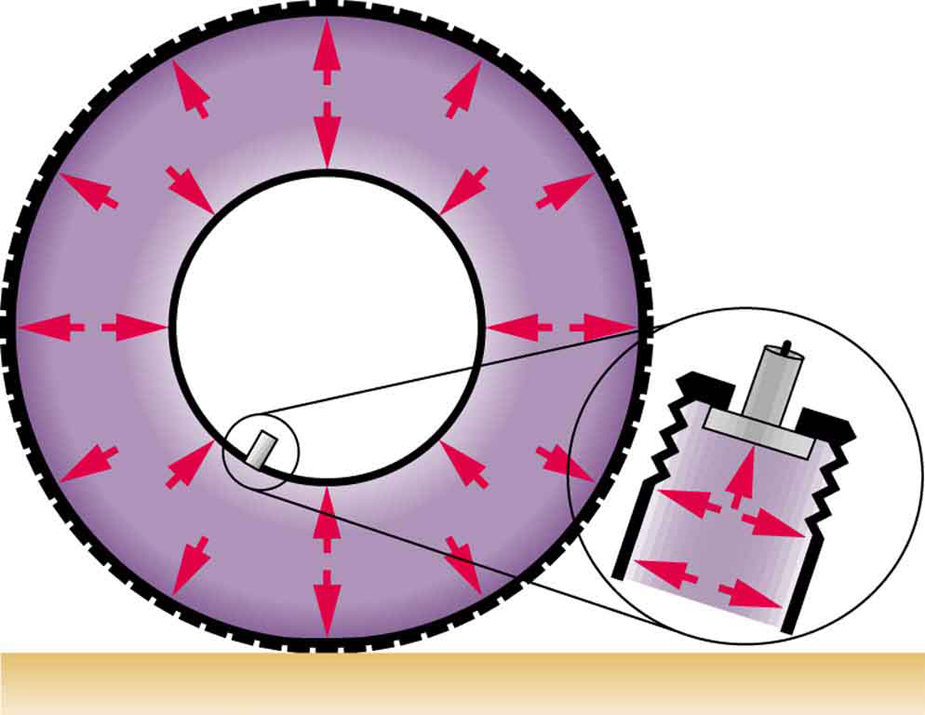
Similarly, in a swimming pool, pressure from the water acts on a swimmer’s body from all directions (see Figure 77.3). The deeper the swimmer, the greater the pressure exerted from below, contributing to buoyancy.
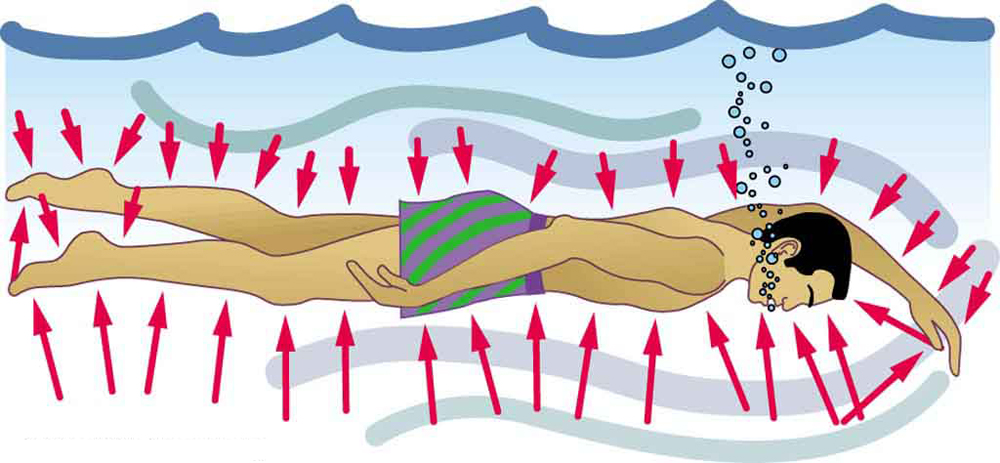
If you’ve ever felt your ears pop during a flight or while diving underwater, you’ve experienced the physiological effects of pressure changes with depth. These changes occur because pressure in a fluid increases with depth due to the increasing weight of fluid above. At sea level, atmospheric pressure results from the weight of the column of air above you. Underwater, pressure increases more rapidly, as both the atmosphere and the water above contribute to the total pressure—and water is about 775 times denser than air. This is why a one-meter dive can be felt more immediately than a 10-story elevator ride.
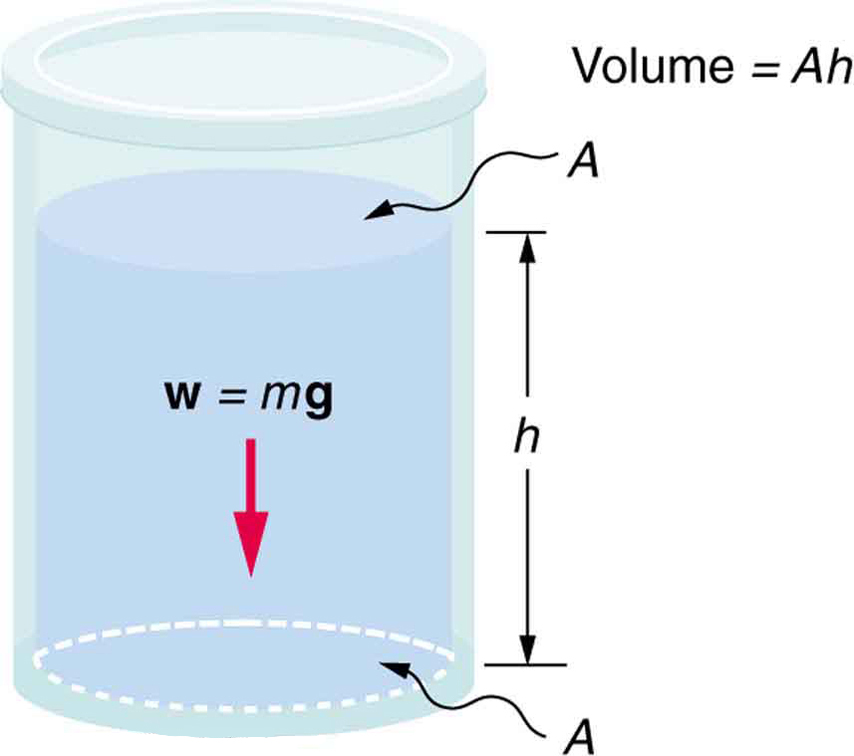
Pressure Due to Fluid Weight
To understand how pressure arises from the weight of a fluid, consider the fluid in a container as shown in Figure 78.1. The pressure at the bottom of the container is due to the weight of the fluid resting on the area of the base:
Here, [latex]m[/latex] is the mass of the fluid, [latex]g[/latex] is the acceleration due to gravity, and [latex]A[/latex] is the area of the container’s base. Substituting [latex]m = \rho V[/latex], where [latex]\rho[/latex] is the fluid density and [latex]V[/latex] is the volume:
So the mass becomes:
Substituting back into the pressure equation:
This relationship tells us that the pressure at a depth [latex]h[/latex] in a fluid is proportional to the fluid’s density and the depth itself:
This formula is valid for any fluid with average density [latex]\rho[/latex] at depth [latex]h[/latex], provided the fluid is either incompressible (like most liquids) or compressibility effects are negligible (as in shallow regions of the atmosphere).
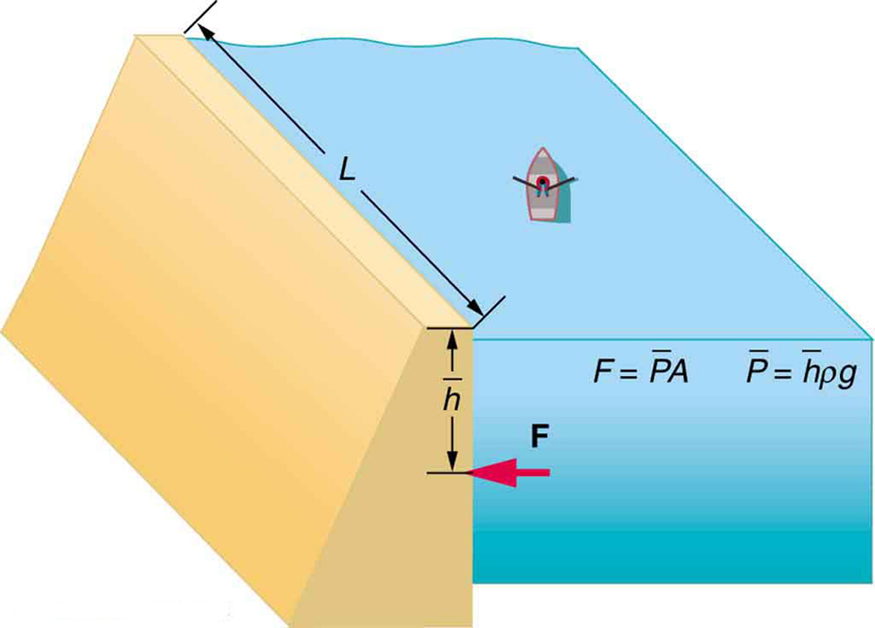
Example 78.1: Pressure on a Dam
A reservoir behind a dam holds water 80.0 m deep. The dam is 500 m wide. (a) What is the average pressure exerted by the water on the dam? (b) What total force does the water exert on the dam wall?
(a) Average Pressure
Using the midpoint depth (40.0 m) to find average pressure:
(b) Force on the Dam
Area of the dam face:
Total force:
Though this is a large force, it is small compared to the weight of the water behind the dam, which is about [latex]1.96 \times 10^{13}\ \text{N}[/latex].
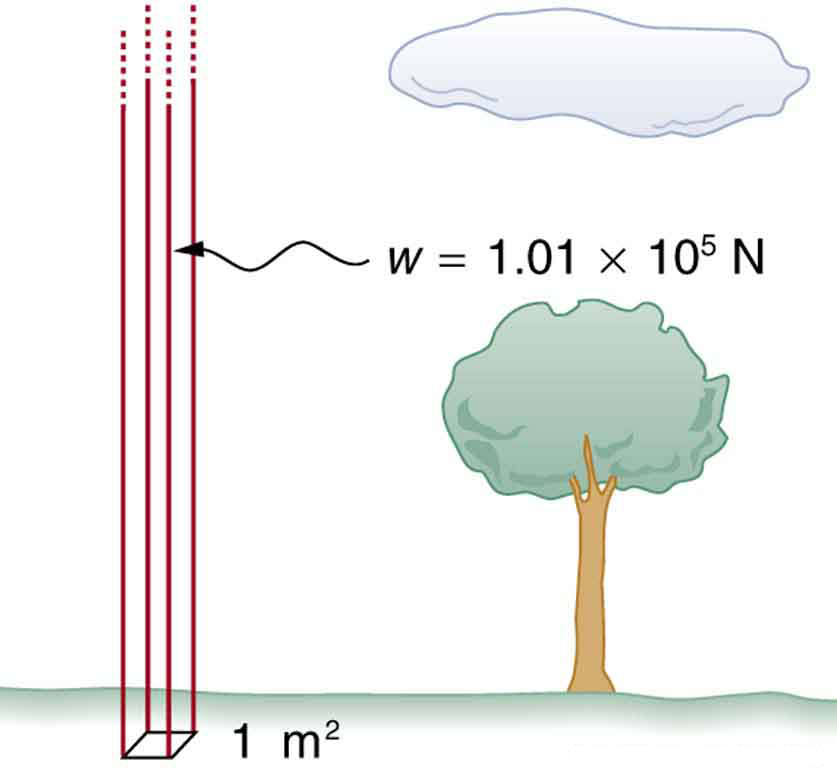
Atmospheric Pressure
Air exerts pressure due to its weight. At sea level, the average atmospheric pressure is:
This is equivalent to the weight of a column of air 1 m² in cross-sectional area extending to the top of the atmosphere.
Example 78.2: Average Density of Air
Estimate the average density of the atmosphere, assuming it extends 120 km above Earth’s surface.
This average density is much lower than the air density at sea level (about 1.29 kg/m³) because air density drops rapidly with altitude due to compressibility.
Example 78.3: Depth Equivalent to Atmospheric Pressure
How deep below the surface of water do you need to go to experience a pressure of 1 atm?
This means that just 10.3 meters of water exerts the same pressure as the entire Earth’s atmosphere. Therefore, at a depth of 10.3 m underwater, the total pressure experienced is 2 atm: 1 atm from the air above the surface and 1 atm from the water above that point.
In fluid mechanics, pressure is defined as force per unit area. This definition explains how pressure can be increased by applying a force directly to a fluid—especially when the fluid is enclosed. For example, when the heart contracts, it increases blood pressure by pushing against the blood within the closed circulatory system. In contrast, fluids in open systems, like rivers, escape when compressed. But in enclosed systems—like blood vessels or hydraulic machines—the pressure cannot escape, making it easier to transmit or amplify forces.
In a closed fluid system, pressure is transmitted throughout the entire fluid. Because fluids are composed of freely moving molecules, any change in pressure is instantly communicated in all directions. This phenomenon is known as Pascal’s principle, named after Blaise Pascal:
Pascal’s Principle
A change in pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and to the walls of the container.
Pascal’s principle is a foundational idea in fluid mechanics and plays an important role in both engineering and biological systems. It explains, for example, how hydraulic lifts in hospitals raise patient beds and how pressure cuffs measure blood pressure. Most importantly, it allows us to understand that total pressure in a fluid is the sum of the pressures from multiple sources—including both fluid weight and any external forces.
Blaise Pascal (1623–1662), the principle’s namesake, was a self-taught mathematician who made major contributions to number theory and probability. He also invented one of the first mechanical calculators and studied how fluids behave under pressure, laying the groundwork for many medical technologies used today.
Applications in Hydraulic Systems
One of the most practical applications of Pascal’s principle is the hydraulic system, which uses an enclosed fluid to transmit force. In medicine, hydraulics appear in devices like patient lifts, surgical tables, and even some dental chairs. In engineering, they are found in car brakes and heavy machinery. The basic concept of a hydraulic system is illustrated in Figure 79.1.
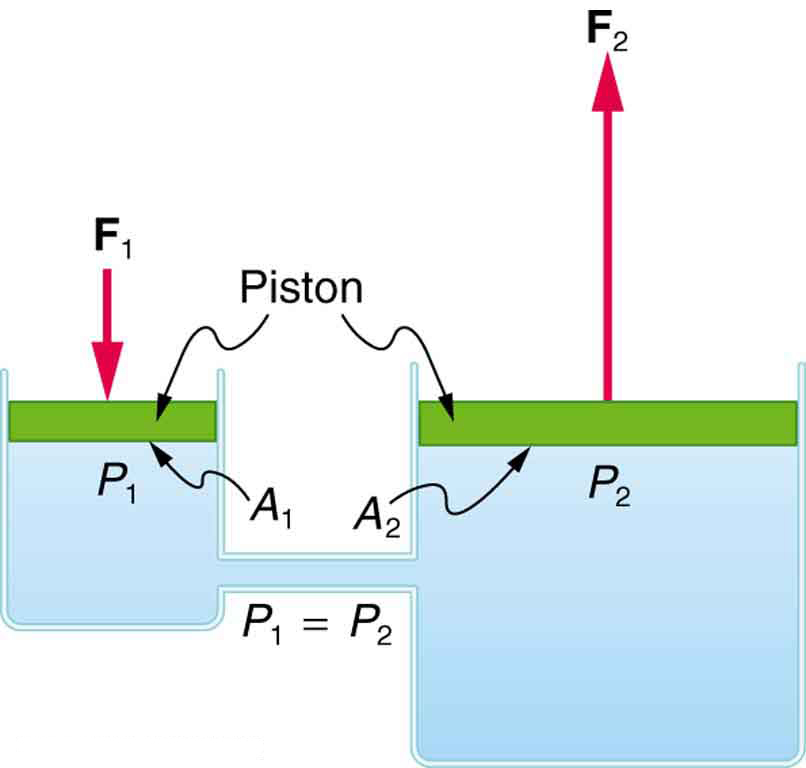
Deriving the Force Relationship in a Hydraulic System
We can derive the relationship between forces in a hydraulic system using Pascal’s principle. Consider two connected cylinders filled with an incompressible fluid. Suppose a force [latex]F_1[/latex] is applied to a small piston of area [latex]A_1[/latex], generating pressure:
According to Pascal’s principle, this pressure is transmitted throughout the fluid, so the pressure at a second piston is also:
Since pressure is force per area, the force at the second piston is:
Equating the two expressions gives:
This equation shows that a small force applied to a small area can be transformed into a much larger force if applied over a larger area. For instance, if [latex]A_2[/latex] is five times greater than [latex]A_1[/latex], the output force [latex]F_2[/latex] will be five times larger than [latex]F_1[/latex].
This mechanical advantage is similar to that of a lever. However, a hydraulic system has the added benefit of being able to transmit force through flexible tubing and around obstacles—allowing for compact and efficient design in both industrial and medical equipment.
Example 79.1 Calculating Force of Slave Cylinders: Pascal Puts on the Brakes
Consider the automobile hydraulic system shown in Figure 79.2.
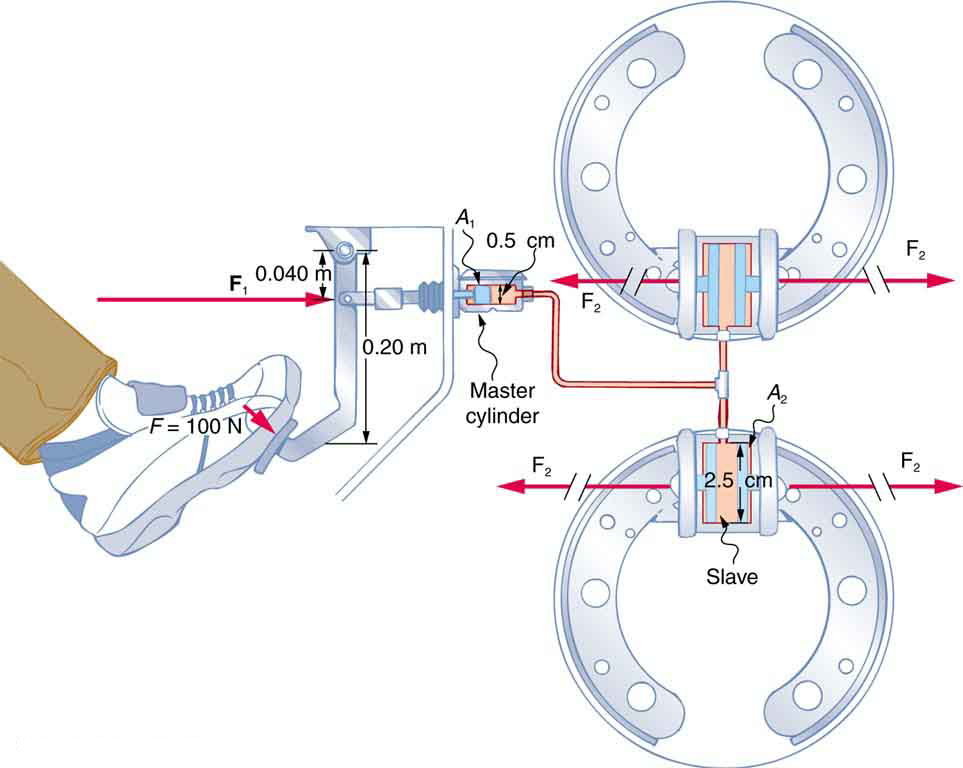
A force of 100 N is applied to the brake pedal, which acts on the cylinder—called the master—through a lever. A force of 500 N is exerted on the master cylinder. (The reader can verify that the force is 500 N using techniques of statics from Applications of Statics, Including Problem-Solving Strategies.) Pressure created in the master cylinder is transmitted to four so-called slave cylinders. The master cylinder has a diameter of 0.500 cm, and each slave cylinder has a diameter of 2.50 cm. Calculate the force [latex]{F}_{2}[/latex] created at each of the slave cylinders.
Strategy
We are given the force [latex]{F}_{1}[/latex] that is applied to the master cylinder. The cross-sectional areas [latex]{A}_{1}[/latex] and [latex]{A}_{2}[/latex] can be calculated from their given diameters. Then [latex]\frac{{F}_{1}}{{A}_{1}}=\frac{{F}_{2}}{{A}_{2}}[/latex] can be used to find the force [latex]{F}_{2}[/latex]. Manipulate this algebraically to get [latex]{F}_{2}[/latex] on one side and substitute known values:
Solution
Pascal’s principle applied to hydraulic systems is given by [latex]\frac{{F}_{1}}{{A}_{1}}=\frac{{F}_{2}}{{A}_{2}}[/latex]:
Discussion
This value is the force exerted by each of the four slave cylinders. Note that we can add as many slave cylinders as we wish. If each has a 2.50-cm diameter, each will exert [latex]1\text{.}\text{25}×{\text{10}}^{4}\phantom{\rule{0.25em}{0ex}}\text{N}\text{.}[/latex]
A simple hydraulic system—much like a simple machine—can increase the applied force, but it cannot perform more work than the work put into it. Recall that work is the product of force and the distance over which the force acts: [latex]W = Fd[/latex]. In hydraulic systems, a force applied to the smaller, master piston causes a larger force to act on the slave piston. However, the slave piston moves a shorter distance. The more slave pistons added, the smaller the distance each one travels.
This concept underlies many real-world technologies, including power brakes and construction machinery such as bulldozers, which often incorporate motorized pumps to do most of the work. Interestingly, some organisms also rely on hydraulic principles. For instance, spiders use hydraulic pressure to extend their legs. The jumping spider, in particular, can leap up to 25 times its body length using hydraulically generated forces!
Making Connections: Conservation of Energy
The conservation of energy principle tells us that no system, including a hydraulic one, can output more energy than it receives. Since energy is transferred via work, this means that the work output from a hydraulic system can never exceed the work input:
In practical systems like power brakes, motorized pumps supply the additional energy needed. Without external energy input, hydraulic systems simply redistribute force and distance according to the constraints of pressure and volume conservation.
Section Summary
- A is a substance that flows and yields to shearing forces. Both liquids and gases are fluids.
- Solids resist deformation because their atoms are fixed in a lattice structure and can only vibrate.
- Liquids flow and take the shape of their container, though they resist compression due to close atomic spacing.
- Gases flow and are easily compressed due to large spacing between atoms and weak intermolecular forces.
- Density is a measure of how much mass is contained in a given volume:
[latex]\rho = \frac{m}{V}[/latex]
- The SI unit for density is [latex]\text{kg/m}^3[/latex], though [latex]\text{g/cm}^3[/latex] or [latex]\text{g/mL}[/latex] are often used in medical contexts.
- Knowing the density of a substance helps predict whether it will float or sink, estimate composition, or calculate mass from volume in real-world problems.
- Pressure is the force per unit perpendicular area over which the force is applied:
[latex]P = \frac{F}{A}[/latex]
- The SI unit of pressure is the pascal: [latex]1~\text{Pa} = 1~\text{N/m}^2[/latex].
- Fluids exert pressure equally in all directions, always perpendicular to the surface they contact.
- Pressure due to the weight of a fluid is given by:
[latex]P = \frac{mg}{A}[/latex]
- Using volume and density, the pressure becomes:
[latex]P = \rho g h[/latex]
- Atmospheric pressure at sea level is approximately:
[latex]P_{\text{atm}} = 1.01 \times 10^5\ \text{Pa} = 101\ \text{kPa}[/latex]
- A change in pressure applied to an enclosed fluid is transmitted undiminished to all parts of the fluid and its container walls (Pascal’s Principle).
- Hydraulic systems use enclosed fluids to apply and transmit forces, often multiplying force while trading off distance moved.
