"

5 Gravity and falling objects

Esperanza Zenon; James Boffenmyer; Mostafa Elaasar; and Shirley Vides

Learning Objectives

  • Describe the effects of gravity on objects in motion.

  • Describe the motion of objects that are in free fall.

  • Calculate the position and velocity of objects in free fall.

  • Explain Earth’s gravitational force on objects.

  • Describe how the Moon’s gravity affects Earth.

  • Understand the concept of weightlessness in orbit.

  • Examine the Cavendish experiment and the measurement of [latex]G[/latex].

  • State and interpret Kepler’s three laws of planetary motion.

  • Derive Kepler’s third law for circular orbits using Newton’s laws.

  • Understand the historical context and limitations of the Ptolemaic model of the universe.

Falling objects form an interesting class of motion problems. For example, we can estimate the depth of a vertical mine shaft by dropping a rock into it and listening for the rock to hit the bottom. By applying the kinematics developed so far to falling objects, we can examine some interesting situations and learn much about gravity in the process.

Gravity

The most remarkable and unexpected fact about falling objects is that, if air resistance and friction are negligible, all objects fall toward the center of Earth with the same constant acceleration, regardless of their mass. This experimentally confirmed result often surprises those accustomed to thinking that heavier objects fall faster.

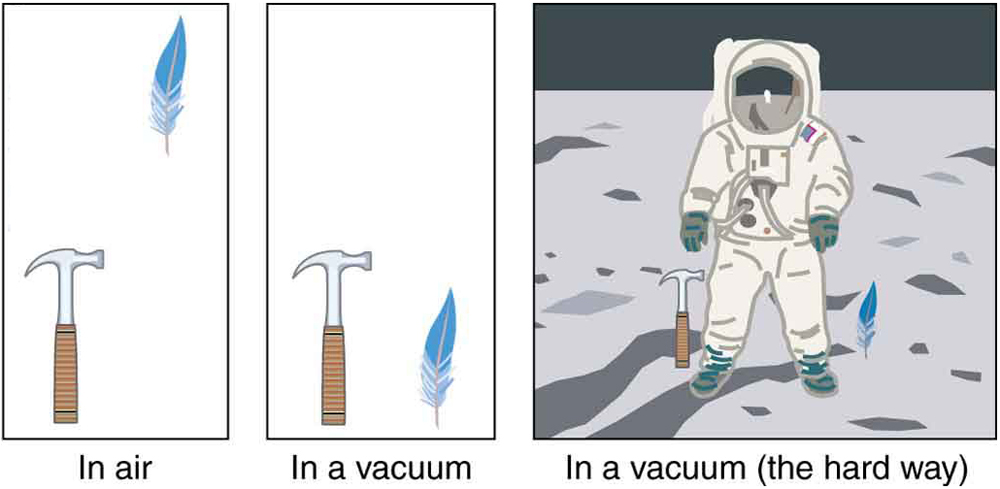
Positions of a feather and hammer over time as they fall on the Moon. The feather and hammer are at the exact same position at each moment in time.
Figure 5.1: A hammer and a feather will fall with the same constant acceleration if air resistance is considered negligible. This general principle holds true anywhere, not just on Earth—as demonstrated by astronaut David R. Scott on the Moon in 1971, where the acceleration due to gravity is only [latex]1.67, \text{m/s}^2[/latex]..

In everyday life, air resistance causes lighter objects to fall slower than heavier ones. For example, a tennis ball will typically hit the ground after a hard baseball dropped from the same height. In idealized situations—those we analyze first—air resistance and friction are ignored, and such an object is said to be in free fall.

The force of gravity causes all free-falling objects to accelerate toward the center of Earth. This acceleration is constant at a given location and is called the acceleration due to gravity, denoted by [latex]g[/latex]:

[latex]g = 9.80, \text{m/s}^2[/latex]

Although the precise value of [latex]g[/latex] varies slightly with location (from about [latex]9.78, \text{m/s}^2[/latex] to [latex]9.83, \text{m/s}^2[/latex]), we will use [latex]9.80, \text{m/s}^2[/latex] as the standard value throughout this text unless otherwise specified.

The direction of [latex]g[/latex] is downward—toward Earth’s center—and it defines what we consider the vertical direction. When working with kinematic equations, the sign of [latex]g[/latex] depends on your choice of coordinate system:

  • If upward is positive: [latex]a = -g = -9.80, \text{m/s}^2[/latex]

  • If downward is positive: [latex]a = g = 9.80, \text{m/s}^2[/latex]

One-Dimensional Motion Involving Gravity

To understand free-fall motion, we start with the simplest scenario: motion that is straight up or down, with no air resistance or friction. This means the velocity is purely vertical.

If an object is dropped (i.e., released without being thrown), then its initial velocity is:

[latex]v_0 = 0[/latex]

Once the object is released, it is in free fall. The acceleration is constant and equal to the magnitude of [latex]g[/latex].

We use [latex]y[/latex] to represent vertical displacement (rather than [latex]x[/latex], which we reserve for horizontal motion). The kinematic equations for vertical free-fall motion under constant acceleration become:

Kinematic Equations for Free-Fall Motion

  1. Velocity after time [latex]t[/latex]:

    [latex]v = v_0 - gt[/latex]

  2. Displacement after time [latex]t[/latex]:

    [latex]y = y_0 + v_0 t - \frac{1}{2} g t^2[/latex]

  3. Velocity-displacement relationship:

    [latex]v^2 = v_0^2 - 2g(y - y_0)[/latex]

Example 5.1: Calculating Position and Velocity of a Falling Object: A Rock Thrown Upward

A person standing on the edge of a high cliff throws a rock straight up with an initial velocity of [latex]13.0\ \text{m/s}[/latex]. The rock misses the edge of the cliff as it falls back to Earth. Calculate the position and velocity of the rock [latex]1.00\ \text{s}[/latex], [latex]2.00\ \text{s}[/latex], and [latex]3.00\ \text{s}[/latex] after it is thrown, neglecting the effects of air resistance.

Strategy

Draw a sketch.

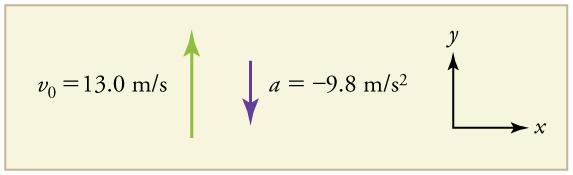
Velocity vector arrow pointing up in the positive y direction, labeled v sub 0 equals thirteen point 0 meters per second. Acceleration vector arrow pointing down in the negative y direction, labeled a equals negative 9 point 8 meters per second squared.
Figure 5.2

We are asked to determine the position [latex]y[/latex] at various times. It is reasonable to take the initial position [latex]{y}_{0}[/latex] to be zero. This problem involves one-dimensional motion in the vertical direction. We use plus and minus signs to indicate direction, with up being positive and down negative. Since up is positive, and the rock is thrown upward, the initial velocity must be positive too. The acceleration due to gravity is downward, so [latex]a[/latex] is negative. It is crucial that the initial velocity and the acceleration due to gravity have opposite signs. Opposite signs indicate that the acceleration due to gravity opposes the initial motion and will slow and eventually reverse it.

Since we are asked for values of position and velocity at three times, we will refer to these as [latex]{y}_{1}[/latex] and [latex]{v}_{1}[/latex]; [latex]{y}_{2}[/latex] and [latex]{v}_{2}[/latex]; and [latex]{y}_{3}[/latex] and [latex]{v}_{3}[/latex].

Solution for Position [latex]{y}_{1}[/latex]

  1. Identify the knowns. We know that [latex]{y}_{0}=0[/latex]; [latex]{v}_{0}=\text{13}\text{.}\text{0 m/s}[/latex]; [latex]a=-g=-9\text{.}{\text{80 m/s}}^{2}[/latex]; and [latex]t=1\text{.}\text{00 s}[/latex].
  2. Identify the best equation to use. We will use [latex]y={y}_{0}+{v}_{0}t+\frac{1}{2}{\text{at}}^{2}[/latex] because it includes only one unknown, [latex]y[/latex] (or [latex]{y}_{1}[/latex], here), which is the value we want to find.
  3. Plug in the known values and solve for [latex]{y}_{1}[/latex].
    [latex]y{}_{1}\text{}=0+\left(\text{13}\text{.}\text{0 m/s}\right)\left(1\text{.}\text{00 s}\right)+\frac{1}{2}\left(-9\text{.}\text{80}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\right){\left(1\text{.}\text{00 s}\right)}^{2}=8\text{.}\text{10}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]

Discussion

The rock is 8.10 m above its starting point at [latex]t=1\text{.}\text{00}[/latex] s, since [latex]{y}_{1}>{y}_{0}[/latex]. It could be moving up or down; the only way to tell is to calculate [latex]{v}_{1}[/latex] and find out if it is positive or negative.

Solution for Velocity [latex]{v}_{1}[/latex]

  1. Identify the knowns. We know that [latex]{y}_{0}=0[/latex]; [latex]{v}_{0}=\text{13}\text{.}\text{0 m/s}[/latex]; [latex]a=-g=-9\text{.}{\text{80 m/s}}^{2}[/latex]; and [latex]t=1\text{.}\text{00 s}[/latex]. We also know from the solution above that [latex]{y}_{1}=8\text{.}\text{10 m}[/latex].
  2. Identify the best equation to use. The most straightforward is [latex]v={v}_{0}-\text{gt}[/latex] (from [latex]v={v}_{0}+\text{at}[/latex], where [latex]a=\text{gravitational acceleration}=-g[/latex]).
  3. Plug in the knowns and solve.
    [latex]{v}_{1}={v}_{0}-\text{gt}=\text{13}\text{.}\text{0 m/s}-\left(9\text{.}{\text{80 m/s}}^{2}\right)\left(1\text{.}\text{00 s}\right)=3\text{.}\text{20 m/s}[/latex]

Discussion

The positive value for [latex]{v}_{1}[/latex] means that the rock is still heading upward at [latex]t=1\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{s}[/latex]. However, it has slowed from its original 13.0 m/s, as expected.

Solution for Remaining Times

The procedures for calculating the position and velocity at [latex]t=2\text{.}\text{00}\phantom{\rule{0.25em}{0ex}}\text{s}[/latex] and [latex]3\text{.}\text{00 s}[/latex] are the same as those above. The results are summarized in Table 5.1 and illustrated in Figure 5.3.

Table 5.1 Results
Time, t Position, y Velocity, v Acceleration, a
[latex]1\text{.}\text{00 s}[/latex] [latex]8\text{.}\text{10 m}[/latex] [latex]3\text{.}\text{20 m/s}[/latex] [latex]-9\text{.}{\text{80 m/s}}^{2}[/latex]
[latex]2\text{.}\text{00 s}[/latex] [latex]6\text{.}\text{40 m}[/latex] [latex]-6\text{.}\text{60 m/s}[/latex] [latex]-9\text{.}{\text{80 m/s}}^{2}[/latex]
[latex]3\text{.}\text{00 s}[/latex] [latex]-5\text{.}\text{10 m}[/latex] [latex]-\text{16}\text{.}\text{4 m/s}[/latex] [latex]-9\text{.}{\text{80 m/s}}^{2}[/latex]

Graphing the data helps us understand it more clearly.

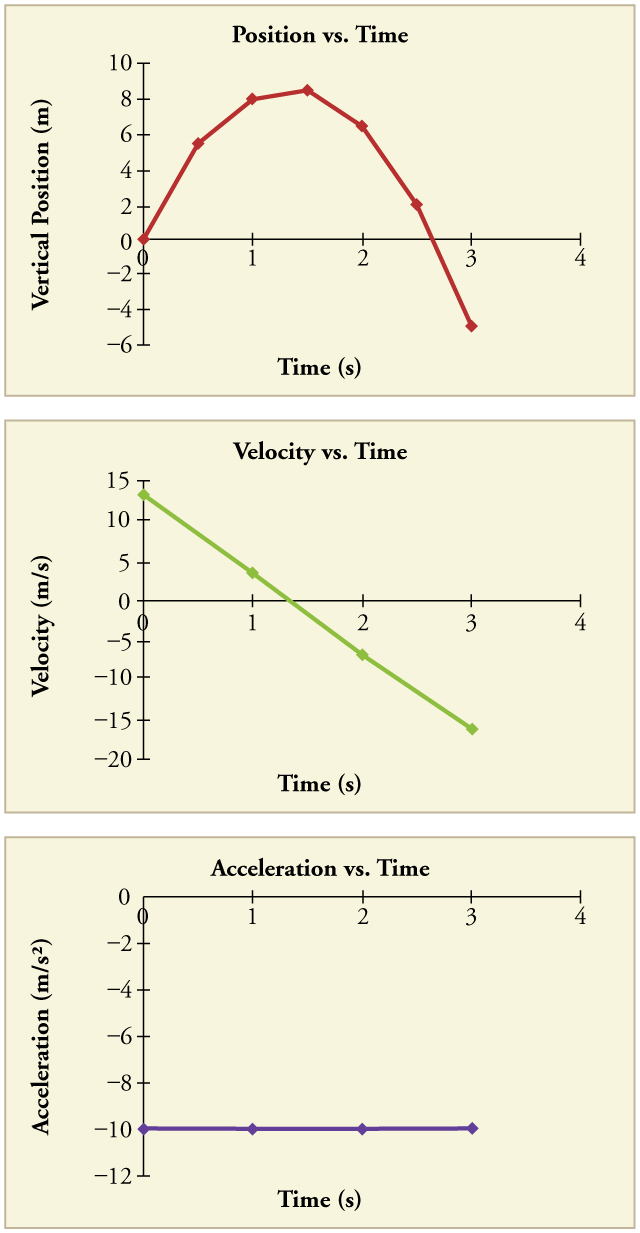
Three panels showing three graphs. The top panel shows a graph of vertical position in meters versus time in seconds. The line begins at the origin and has a positive slope that decreases over time until it hits a turning point between seconds 1 and 2. After that it has a negative slope that increases over time. The middle panel shows a graph of velocity in meters per second versus time in seconds. The line is straight, with a negative slope, beginning at time zero velocity of thirteen meters per second and ending at time 3 seconds with a velocity just over negative sixteen meters per second. The bottom panel shows a graph of acceleration in meters per second squared versus time in seconds. The line is straight and flat at a y value of negative 9 point 80 meters per second squared from time 0 to time 3 seconds.
Figure 5.3: Vertical position, vertical velocity, and vertical acceleration vs. time for a rock thrown vertically up at the edge of a cliff. Notice that velocity changes linearly with time and that acceleration is constant. Misconception Alert! Notice that the position vs. time graph shows vertical position only. It is easy to get the impression that the graph shows some horizontal motion—the shape of the graph looks like the path of a projectile. But this is not the case; the horizontal axis is time, not space. The actual path of the rock in space is straight up, and straight down.

Discussion

The interpretation of these results is important. At 1.00 s the rock is above its starting point and heading upward, since [latex]{y}_{1}[/latex] and [latex]{v}_{1}[/latex] are both positive. At 2.00 s, the rock is still above its starting point, but the negative velocity means it is moving downward. At 3.00 s, both [latex]{y}_{3}[/latex] and [latex]{v}_{3}[/latex] are negative, meaning the rock is below its starting point and continuing to move downward. Notice that when the rock is at its highest point (at 1.5 s), its velocity is zero, but its acceleration is still [latex]-9\text{.}{\text{80 m/s}}^{2}[/latex]. Its acceleration is [latex]-9\text{.}{\text{80 m/s}}^{2}[/latex] for the whole trip—while it is moving up and while it is moving down. Note that the values for [latex]y[/latex] are the positions (or displacements) of the rock, not the total distances traveled. Finally, note that free-fall applies to upward motion as well as downward. Both have the same acceleration—the acceleration due to gravity, which remains constant the entire time. Astronauts training in the famous Vomit Comet, for example, experience free-fall while arcing up as well as down, as we will discuss in more detail later.

Making Connections: Take-Home Experiment—Reaction Time

You can estimate your reaction time using a simple home experiment and a ruler.

Materials

  • A ruler (30 cm or longer)

  • A friend or classmate

Procedure

  1. Sit with your hand open and thumb and index finger about [latex]1\ \text{cm}[/latex] apart.

  2. Have your friend hold the ruler vertically so that the [latex]0\ \text{cm}[/latex] mark is aligned between your fingers.

  3. Without warning, your friend drops the ruler. Try to catch it as quickly as possible using your fingers.

  4. Record the distance the ruler falls before you catch it. For example, you might catch it at the [latex]18\ \text{cm}[/latex] mark.

Step 1: Estimate Your Reaction Time

The distance [latex]d[/latex] the ruler falls is related to the time [latex]t[/latex] it takes to fall using the kinematic equation:

[latex]d = \frac{1}{2}gt^2[/latex]

Solve for [latex]t[/latex]:

[latex]t = \sqrt{\frac{2d}{g}}[/latex]

Assuming [latex]g = 9.80\ \text{m/s}^2[/latex] and converting [latex]d = 18\ \text{cm} = 0.18\ \text{m}[/latex]:

[latex]t = \sqrt{\frac{2(0.18\ \text{m})}{9.80\ \text{m/s}^2}} = \sqrt{0.0367\ \text{s}^2} \approx 0.191\ \text{s}[/latex]

So your reaction time is approximately 0.19 seconds.

Step 2: Distance Traveled in a Car

Assume you are driving at [latex]30\ \text{m/s}[/latex] (about 108 km/h or 67 mph). If the time it takes your foot to move from the gas pedal to the brake is twice your reaction time, then:

[latex]t = 2 \times 0.191\ \text{s} = 0.382\ \text{s}[/latex]

Use:

[latex]\text{distance} = \text{speed} \times \text{time}[/latex]

[latex]d = (30\ \text{m/s})(0.382\ \text{s}) \approx 11.5\ \text{m}[/latex]

So, your car would travel approximately 11.5 meters before you even begin braking.

Reflection

This quick experiment demonstrates the importance of reaction time in real-world situations such as driving. Even a fraction of a second delay can mean traveling several meters before you start to respond. This is why safe following distances are crucial.

Example 5.2: Calculating Velocity of a Falling Object: A Rock Thrown Down

What happens if the person on the cliff throws the rock straight down, instead of straight up? To explore this question, calculate the velocity of the rock when it is 5.10 m below the starting point, and has been thrown downward with an initial speed of 13.0 m/s.

Strategy

Draw a sketch.

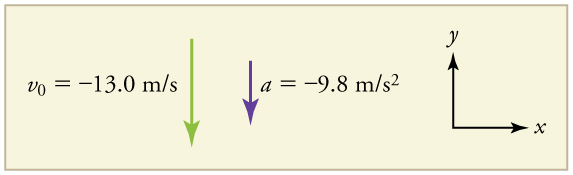
Velocity vector arrow pointing down in the negative y direction and labeled v sub zero equals negative thirteen point 0 meters per second. Acceleration vector arrow also pointing down in the negative y direction, labeled a equals negative 9 point 80 meters per second squared.
Figure 5.4

Since up is positive, the final position of the rock will be negative because it finishes below the starting point at [latex]{y}_{0}=0[/latex]. Similarly, the initial velocity is downward and therefore negative, as is the acceleration due to gravity. We expect the final velocity to be negative since the rock will continue to move downward.

Solution

  1. Identify the knowns. [latex]{y}_{0}=0[/latex];
    [latex]{y}_{1}=-5\text{.}\text{10 m}[/latex];
    [latex]{v}_{0}=-\text{13}\text{.0 m/s}[/latex];
    [latex]a=-g=-9\text{.}\text{80 m}{\text{/s}}^{2}[/latex].
  2. Choose the kinematic equation that makes it easiest to solve the problem. The equation [latex]{v}^{2}={v}_{0}^{2}+2a\left(y-{y}_{0}\right)[/latex] works well because the only unknown in it is [latex]v[/latex]. (We will plug [latex]{y}_{1}[/latex] in for [latex]y[/latex].)
  3. Enter the known values
    [latex]{v}^{2}={\left(-\text{13}\text{.}\text{0 m/s}\right)}^{2}+2\left(-9\text{.}{\text{80 m/s}}^{2}\right)\left(-5\text{.}\text{10 m}-\text{0 m}\right)=\text{268}\text{.}{\text{96 m}}^{2}{\text{/s}}^{2},[/latex]
    where we have retained extra significant figures because this is an intermediate result.
    Taking the square root, and noting that a square root can be positive or negative, gives
    [latex]v=±\text{16}\text{.4 m/s}.[/latex]

    The negative root is chosen to indicate that the rock is still heading down. Thus,

    [latex]v=-\text{16}\text{.4 m/s}.[/latex]

Discussion

Note that this is exactly the same velocity the rock had at this position when it was thrown straight upward with the same initial speed. (See Example 5.1 and Figure 5.5(a).) This is not a coincidental result. Because we only consider the acceleration due to gravity in this problem, the speed of a falling object depends only on its initial speed and its vertical position relative to the starting point. For example, if the velocity of the rock is calculated at a height of 8.10 m above the starting point  when the initial velocity is 13.0 m/s straight up, a result of [latex]±3\text{.}\text{20 m/s}[/latex] is obtained. Here both signs are meaningful; the positive value occurs when the rock is at 8.10 m and heading up, and the negative value occurs when the rock is at 8.10 m and heading back down. It has the same speed but the opposite direction.

 

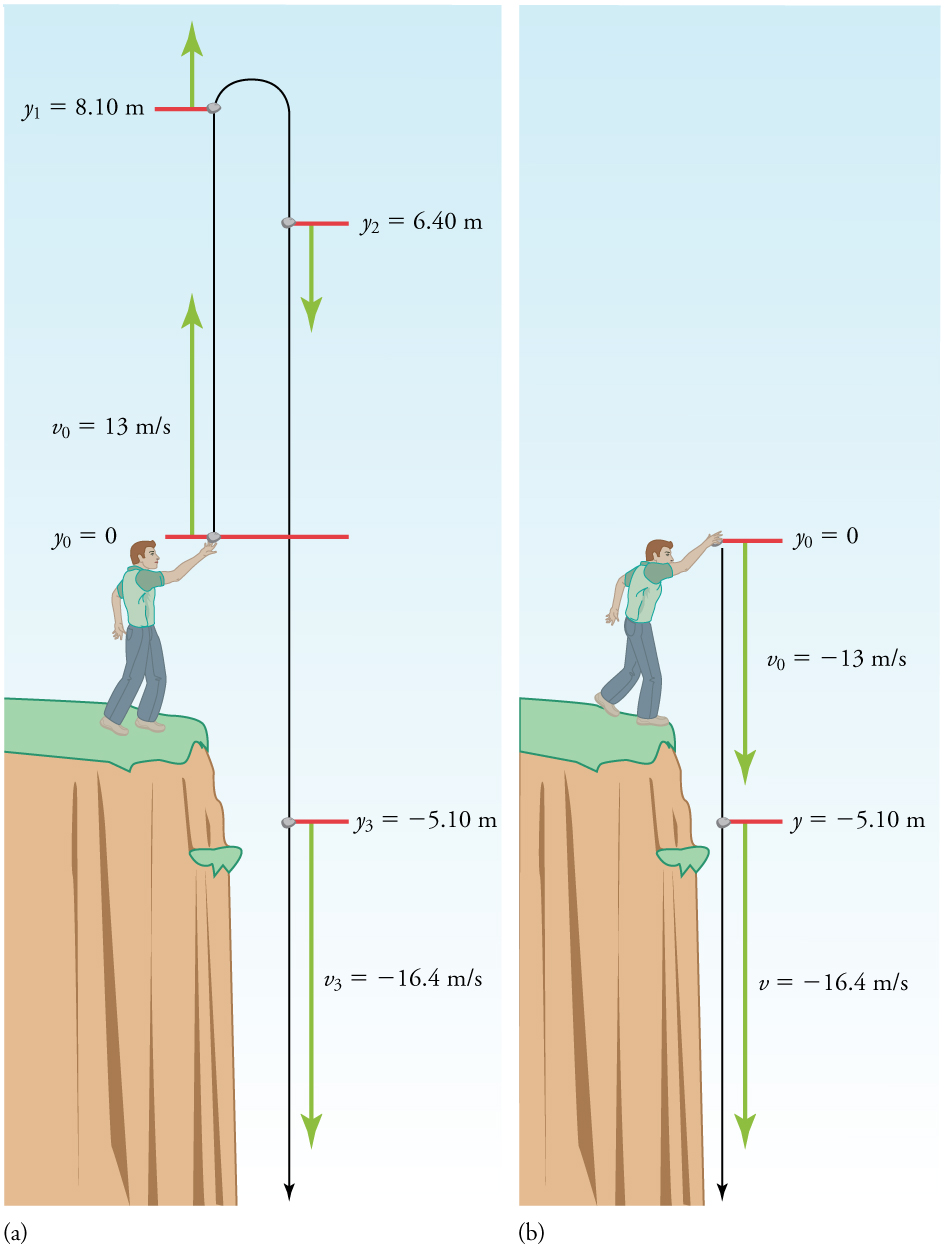
Two figures are shown. At left, a man standing on the edge of a cliff throws a rock straight up with an initial speed of thirteen meters per second. At right, the man throws the rock straight down with a speed of thirteen meters per second. In both figures, a line indicates the rock’s trajectory. When the rock is thrown straight up, it has a speed of minus sixteen point four meters per second at minus five point one zero meters below the point where the man released the rock. When the rock is thrown straight down, the velocity is the same at this position.
Figure 5.5: (a) A person throws a rock straight up. The arrows are velocity vectors at 0, 1.00, 2.00, and 3.00 s. (b) A person throws a rock straight down from a cliff with the same initial speed as before. Note that at the same distance below the point of release, the rock has the same velocity in both cases.

 

Another way to look at it is this: When the rock is thrown up with an initial velocity of [latex]\text{13}\text{.0 m/s}[/latex]. It rises and then falls back down. When its position is [latex]y=0[/latex] on its way back down, its velocity is [latex]-\text{13}\text{.0 m/s}[/latex]. That is, it has the same speed on its way down as on its way up. We would then expect its velocity at a position of [latex]y=-5\text{.}\text{10 m}[/latex] to be the same whether we have thrown it upwards at [latex]+\text{13}\text{.0 m/s}[/latex] or thrown it downwards at [latex]-\text{13}\text{.0 m/s}[/latex]. The velocity of the rock on its way down from [latex]y=0[/latex] is the same whether we have thrown it up or down to start with, as long as the speed with which it was initially thrown is the same.

Example 5.3: Find g from Data on a Falling Object

The acceleration due to gravity on Earth differs slightly from place to place, depending on topography (e.g., whether you are on a hill or in a valley) and subsurface geology (whether there is dense rock like iron ore as opposed to light rock like salt beneath you.) The precise acceleration due to gravity can be calculated from data taken in an introductory physics laboratory course. An object, usually a metal ball for which air resistance is negligible, is dropped and the time it takes to fall a known distance is measured. See, for example, Figure 5.6. Very precise results can be produced with this method if sufficient care is taken in measuring the distance fallen and the elapsed time.

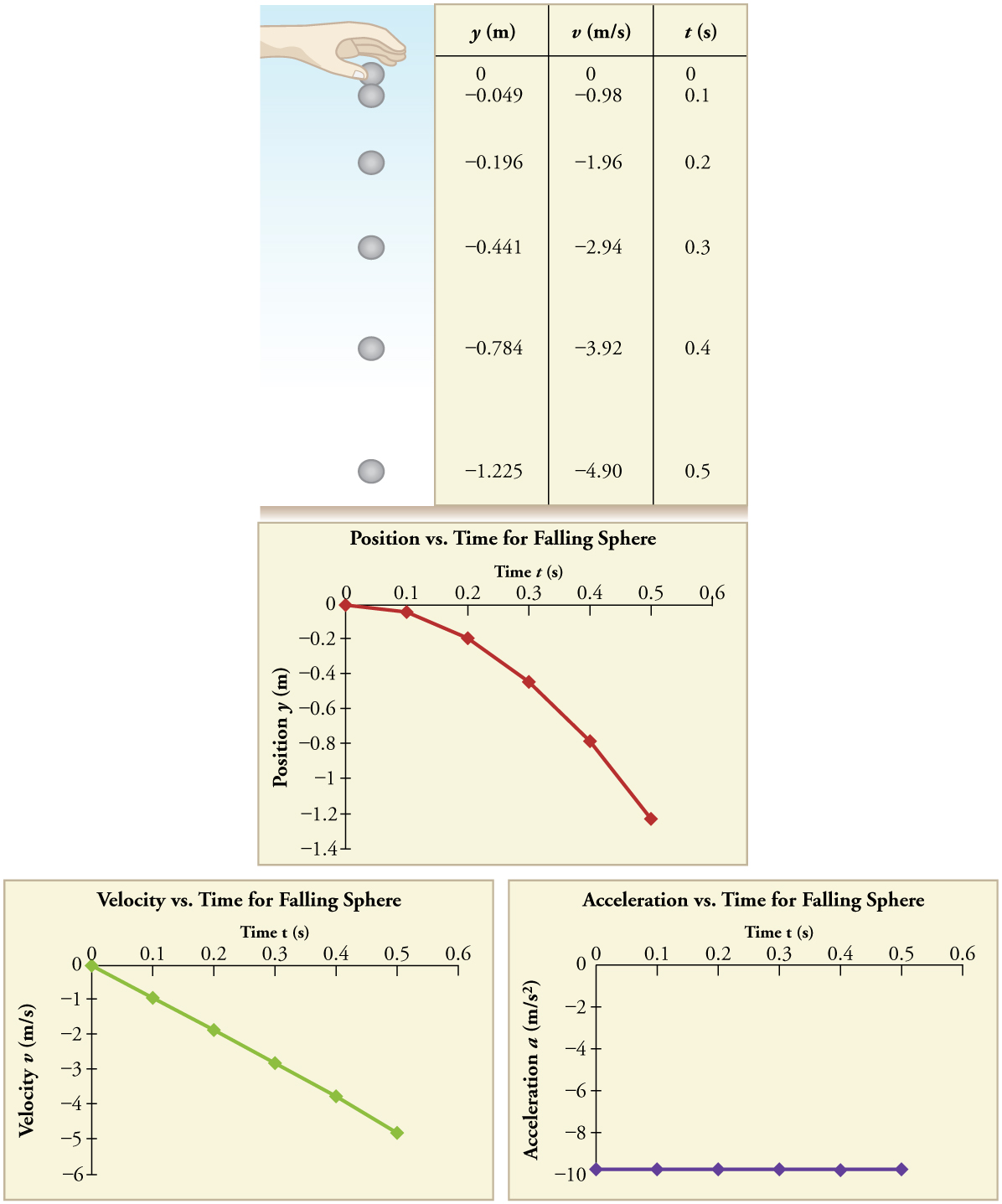
Figure has four panels. The first panel (on the top) is an illustration of a ball falling toward the ground at intervals of one tenth of a second. The space between the vertical position of the ball at one time step and the next increases with each time step. At time equals 0, position and velocity are also 0. At time equals 0 point 1 seconds, y position equals negative 0 point 049 meters and velocity is negative 0 point 98 meters per second. At 0 point 5 seconds, y position is negative 1 point 225 meters and velocity is negative 4 point 90 meters per second. The second panel (in the middle) is a line graph of position in meters versus time in seconds. Line begins at the origin and slopes down with increasingly negative slope. The third panel (bottom left) is a line graph of velocity in meters per second versus time in seconds. Line is straight, beginning at the origin and with a constant negative slope. The fourth panel (bottom right) is a line graph of acceleration in meters per second squared versus time in seconds. Line is flat, at a constant y value of negative 9 point 80 meters per second squared.
Figure 5.6: Positions and velocities of a metal ball released from rest when air resistance is negligible. Velocity is seen to increase linearly with time while displacement increases with time squared. Acceleration is a constant and is equal to gravitational acceleration.

Suppose the ball falls 1.0000 m in 0.45173 s. Assuming the ball is not affected by air resistance, what is the precise acceleration due to gravity at this location?

Strategy

Draw a sketch.

The figure shows a green dot labeled v sub zero equals zero meters per second, a purple downward pointing arrow labeled a equals question mark, and an x y coordinate system with the y axis pointing vertically up and the x axis pointing horizontally to the right.
Figure 5.7

We need to solve for acceleration [latex]a[/latex]. Note that in this case, displacement is downward and therefore negative, as is acceleration.

Solution

  1. Identify the knowns. [latex]{y}_{0}=0[/latex];
    [latex]y=–1\text{.0000 m}[/latex];
    [latex]t=0\text{.45173}[/latex]; [latex]{v}_{0}=0[/latex].
  2. Choose the equation that allows you to solve for [latex]a[/latex] using the known values.
    [latex]y={y}_{0}+{v}_{0}t+\frac{1}{2}{\text{at}}^{2}[/latex]
  3. Substitute 0 for [latex]{v}_{0}[/latex] and rearrange the equation to solve for [latex]a[/latex]. Substituting 0 for [latex]{v}_{0}[/latex] yields
    [latex]y={y}_{0}+\frac{1}{2}{\text{at}}^{2}\text{.}[/latex]

    Solving for [latex]a[/latex] gives

    [latex]a=\frac{2\left(y-{y}_{0}\right)}{{t}^{2}}\text{.}[/latex]
  4. Substitute known values yields
    [latex]a=\frac{2\left(-1\text{.}\text{0000 m – 0}\right)}{\left(0\text{.}\text{45173 s}\right)}^{2}=-9\text{.}{\text{8010 m/s}}^{2},[/latex]

    so, because [latex]a=-g[/latex] with the directions we have chosen,

    [latex]g=9\text{.}{\text{8010 m/s}}^{2}.[/latex]

Discussion

The negative value for [latex]a[/latex] indicates that the gravitational acceleration is downward, as expected. We expect the value to be somewhere around the average value of [latex]9\text{.}{\text{80 m/s}}^{2}[/latex], so [latex]9\text{.}{\text{8010 m/s}}^{2}[/latex] makes sense. Since the data going into the calculation are relatively precise, this value for [latex]g[/latex] is more precise than the average value of [latex]9\text{.}{\text{80 m/s}}^{2}[/latex]; it represents the local value for the acceleration due to gravity.

Check Your Understanding

A chunk of ice breaks off a glacier and falls [latex]30.0\ \text{m}[/latex] before it hits the water. Assuming it falls freely (that is, with no air resistance), how long does it take to hit the water?

We are given:

  • Initial position: [latex]y_0 = 0[/latex]

  • Final position: [latex]y = -30.0\ \text{m}[/latex]

  • Initial velocity: [latex]v_0 = 0[/latex] (the object is dropped)

  • Acceleration: [latex]a = -g = -9.80\ \text{m/s}^2[/latex]

We use the following kinematic equation:

[latex]y = y_0 + v_0 t + \frac{1}{2} a t^2[/latex]

Substitute known values:

[latex]-30.0 = 0 + 0 - \frac{1}{2}(9.80)t^2[/latex]

Solve for [latex]t[/latex]:

[latex]t^2 = \frac{2(-30.0)}{-9.80} = \frac{-60.0}{-9.80} = 6.12[/latex]

[latex]t = \sqrt{6.12} \approx 2.47\ \text{s}[/latex]

Answer: It takes approximately [latex]2.5\ \text{s}[/latex] for the piece of ice to hit the water.

PhET Explorations: Equation Grapher

Explore how different polynomial terms contribute to the shape of a graph. With the Equation Grapher simulation, you can:

  • Graph equations like [latex]y = bx[/latex], [latex]y = ax^2[/latex], and more.

  • Adjust constants to see how they affect the curve.

  • Combine terms to visualize full polynomial functions.

Gravity in Everyday Life and Astronomy

From aching feet to falling apples to orbiting moons, all these phenomena are governed by gravity—the attractive force between all masses. This force holds planets in orbit, forms galaxies, and even affects biological functions like posture and blood circulation.

Sir Isaac Newton was the first to formulate a universal law that explained both terrestrial and celestial motion using a single principle. The legend of the falling apple (Figure 5.8) symbolizes his insight: if gravity acts on an apple, could it not also reach the Moon—and beyond?

The figure shows a graphic image of a person sitting under a tree carefully looking toward an apple falling from the tree above him. There is a view of a river behind him and an image of the Sun in the sky.
Figure 5.8: According to early accounts, Newton was inspired to make the connection between falling bodies and astronomical motions when he saw an apple fall from a tree and realized that if the gravitational force could extend above the ground to a tree, it might also reach the Sun. The inspiration of Newton’s apple is a part of worldwide folklore and may even be based in fact. Great importance is attached to it because Newton’s universal law of gravitation and his laws of motion answered very old questions about nature and gave tremendous support to the notion of underlying simplicity and unity in nature. Scientists still expect underlying simplicity to emerge from their ongoing inquiries into nature.

Newton’s Law of Universal Gravitation

Newton’s universal law of gravitation states:

Every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers.

Mathematically, the gravitational force [latex]F[/latex] between two objects of mass [latex]m[/latex] and [latex]M[/latex], separated by a distance [latex]r[/latex], is:

[latex]F = G \frac{mM}{r^2}[/latex]

  • [latex]F[/latex]: gravitational force in newtons (N)

  • [latex]G[/latex]: gravitational constant,
    [latex]G = 6.674 \times 10^{-11} , \frac{\text{N} \cdot \text{m}^2}{\text{kg}^2}[/latex]

  • [latex]m, M[/latex]: masses in kilograms (kg)

  • [latex]r[/latex]: distance between centers of mass in meters (m)

This relationship is illustrated in Figure 5.9, where the gravitational force acts along the line connecting the centers of mass of the two bodies. Consistent with Newton’s third law, both bodies experience forces of equal magnitude in opposite directions.

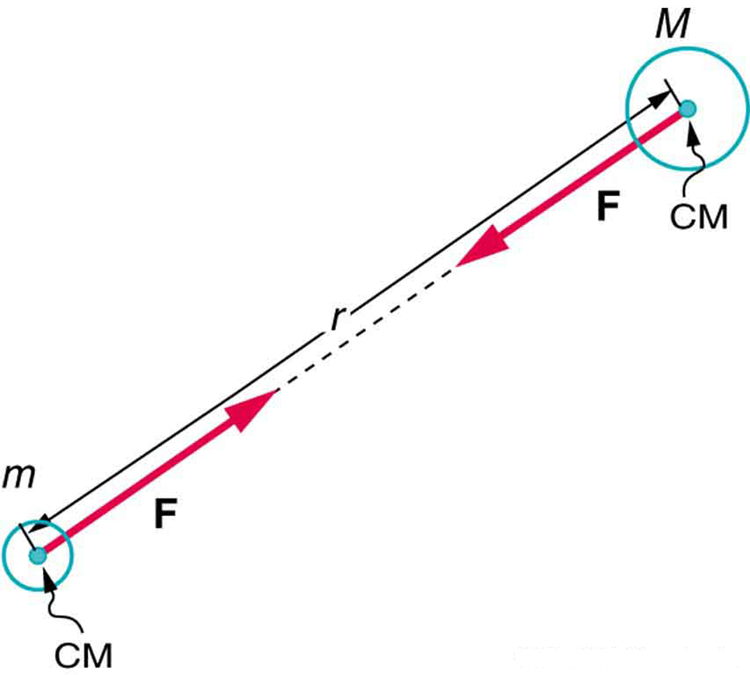
The given figure shows two circular objects, one with a larger mass M on the right side, and another with a smaller mass m on the left side. A point in the center of each object is shown, with both depicting the center of mass of the objects at these points. A line is drawn joining the center of the objects and is labeled as r. Two red arrows, one each from both the center of the objects, are drawn toward each other and are labeled as F, the magnitude of the gravitational force on both the objects.
Figure 5.9: Gravitational attraction is along a line joining the centers of mass of these two bodies. The magnitude of the force is the same on each, consistent with Newton’s third law.

Center of Mass and Simplification

For extended bodies like planets or humans, we assume their mass is concentrated at a point—their center of mass. This simplifies gravitational calculations, particularly when the distance between objects is much larger than their size.

Deriving the Acceleration Due to Gravity [latex]g[/latex]

Let’s connect Newton’s law of gravitation to the acceleration of falling objects on Earth. Recall that weight is defined as:

[latex]F = mg[/latex]

Substituting into Newton’s gravitational equation:

[latex]mg = G \frac{mM}{r^2}[/latex]

Solving for [latex]g[/latex]:

[latex]g = G \frac{M}{r^2}[/latex]

Using Earth’s values:

  • [latex]M = 5.98 \times 10^{24} , \text{kg}[/latex]

  • [latex]r = 6.38 \times 10^6 , \text{m}[/latex] (Earth’s radius)

[latex]g = \left(6.67 \times 10^{-11} , \frac{\text{N} \cdot \text{m}^2}{\text{kg}^2} \right) \frac{5.98 \times 10^{24} , \text{kg}}{(6.38 \times 10^6 , \text{m})^2} = 9.80 , \text{m/s}^2[/latex]

This result is consistent with the observed acceleration due to gravity on Earth, and it shows that all objects—regardless of mass—fall at the same rate near Earth’s surface.

Figure 5.10 shows the gravitational interaction between Earth and an object, emphasizing that [latex]r[/latex] is the distance to Earth’s center.

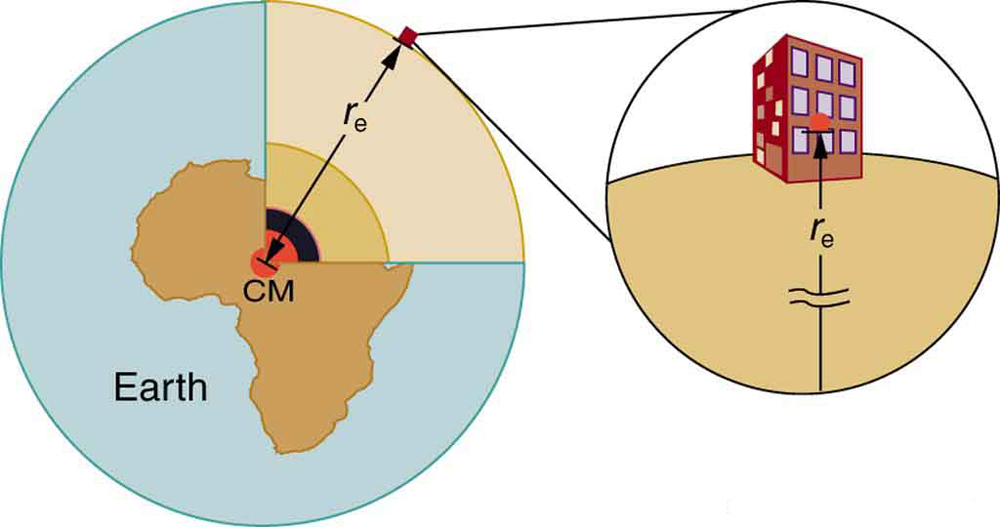
The given figure shows two circular images side by side. The bigger circular image on the left shows the Earth, with a map of Africa over it in the center, and the first quadrant in the circle being a line diagram showing the layers beneath Earth’s surface. The second circular image shows a house over the Earth’s surface and a vertical line arrow from its center to the downward point in the circle as its radius distance from the Earth’s surface. A similar line showing the Earth’s radius is also drawn in the first quadrant of the first image in a slanting way from the center point to the circle path.
Figure 5.10: The distance between the centers of mass of Earth and an object on its surface is very nearly the same as the radius of Earth, because Earth is so much larger than the object.

Misconception Alert: Equal Force on Unequal Masses

One common misunderstanding is that heavier objects exert more gravitational force. While heavier objects do exert larger forces on lighter ones, Newton’s third law ensures the forces are equal and opposite. The difference lies in the acceleration, which is smaller for the more massive body.

Take-Home Experiment

Try dropping a marble, a spoon, and a ball from the same height. Do they hit the ground at the same time? Likely, yes. Now try a sheet of paper—its slower fall is due to air resistance, not gravitational mass.

Broader Context: Gravitational Force in Modern Physics

Although Newton’s law remains powerful, modern physics—especially Einstein’s General Relativity—treats gravity as the curvature of space-time rather than a force. Still, Newton’s equation accurately predicts planetary motion and everyday gravitational effects.

Preview of the Cavendish Experiment

In the next section, we’ll explore Henry Cavendish’s experiment, which provided the first accurate measurement of the gravitational constant [latex]G[/latex], enabling scientists to weigh Earth and validate Newton’s equation with laboratory-scale data.

Example 5.4: Earth’s Gravitational Force Is the Centripetal Force Making the Moon Move in a Curved Path

  1. Find the acceleration due to Earth’s gravity at the distance of the Moon.
  2. Calculate the centripetal acceleration needed to keep the Moon in its orbit (assuming a circular orbit about a fixed Earth), and compare it with the value of the acceleration due to Earth’s gravity that you have just found.

Strategy for (a)

This calculation is the same as the one finding the acceleration due to gravity at Earth’s surface, except that [latex]r[/latex]is the distance from the center of Earth to the center of the Moon. The radius of the Moon’s nearly circular orbit is [latex]3\text{.}\text{84}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex].

Solution for (a)

Substituting known values into the expression for [latex]g[/latex] found above, remembering that [latex]M[/latex] is the mass of Earth not the Moon, yields

[latex]\begin{array}{lll}g& =& G\frac{M}{{r}^{2}}=(6\text{.}\text{67}×{\text{10}}^{-\text{11}}\frac{\text{N}\cdot {\text{m}}^{2}}{{\text{kg}}^{2}})×\frac{5\text{.}\text{98}×{\text{10}}^{\text{24}}\phantom{\rule{0.25em}{0ex}}\text{kg}}{(3\text{.}\text{84}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m}{)}^{2}}\\ & =& 2\text{.}\text{70}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m/s.}}^{2}\end{array}[/latex]

Strategy for (b)

Centripetal acceleration can be calculated using either form of

[latex]\begin{array}{c}{a}_{c}=\frac{{v}^{2}}{r}\\ {a}_{c}={\mathrm{r\omega }}^{2}\end{array}[/latex]

We choose to use the second form:

[latex]{a}_{c}={\mathrm{r\omega }}^{2}\text{,}[/latex]

where [latex]\omega[/latex] is the angular velocity of the Moon about Earth.

Solution for (b)

Given that the period (the time it takes to make one complete rotation) of the Moon’s orbit is 27.3 days, (d) and using

[latex]1 d×24\frac{\text{hr}}{\text{d}}×60\frac{min}{\text{hr}}×60\frac{s}{\text{min}}=\text{86,400 s}[/latex]

we see that

[latex]\omega =\frac{\text{Δ}\theta }{\text{Δ}t}=\frac{2\pi \phantom{\rule{0.25em}{0ex}}\text{rad}}{(\text{27}\text{.}\text{3 d})(\text{86,400 s/d})}=2\text{.}\text{66}×{\text{10}}^{-6}\frac{\text{rad}}{\text{s}}.[/latex]

The centripetal acceleration is

[latex]\begin{array}{lll}{a}_{c}& =& {\mathrm{r\omega }}^{2}=(3\text{.}\text{84}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m})(2\text{.}\text{66}×{\text{10}}^{-6}\phantom{\rule{0.25em}{0ex}}\text{rad/s}{)}^{2}\\ & =& \text{2.72}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}{\text{m/s.}}^{2}\end{array}[/latex]

The direction of the acceleration is toward the center of the Earth.

Discussion

The centripetal acceleration of the Moon found in (b) differs by less than 1% from the acceleration due to Earth’s gravity found in (a). This agreement is approximate because the Moon’s orbit is slightly elliptical, and Earth is not stationary (rather the Earth-Moon system rotates about its center of mass, which is located some 1700 km below Earth’s surface). The clear implication is that Earth’s gravitational force causes the Moon to orbit Earth.

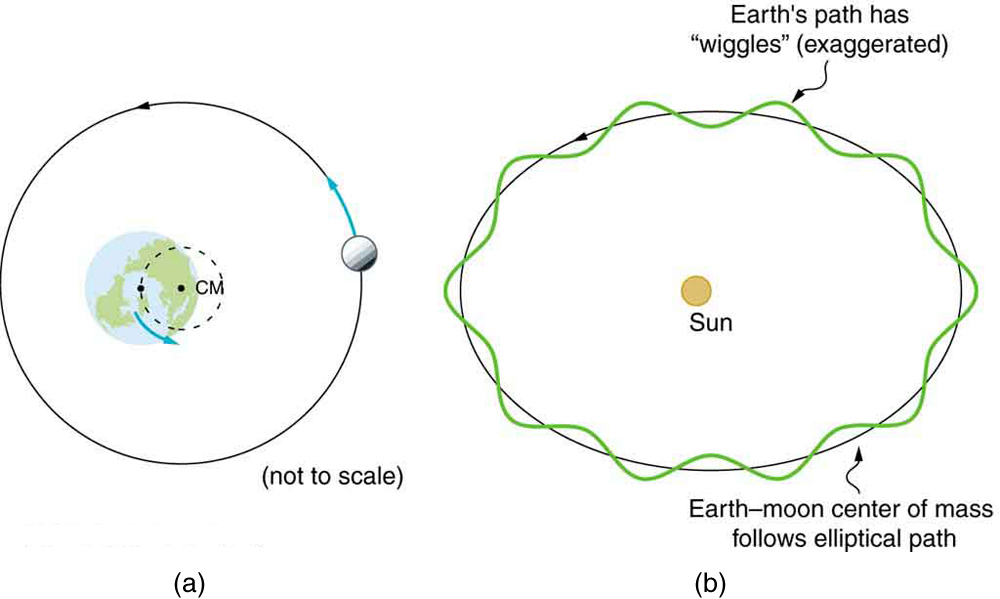
Earth and Moon: Mutual Gravitation

Although it seems the Moon orbits a stationary Earth, this is not entirely true. According to Newton’s third law, the gravitational force the Earth exerts on the Moon is matched by an equal and opposite force the Moon exerts on Earth.

Both Earth and the Moon orbit their common center of mass, which lies inside Earth but not at its exact center (Figure 5.11). This mutual orbit causes small “wiggles” in Earth’s path around the Sun—subtle variations observable in the motion of stars that reveal the presence of exoplanets orbiting them.

Figure a shows the Earth and the Moon around it orbiting in a circular path shown here as a circle around the Earth with an arrow over it showing the counterclockwise direction of the Moon. The center of mass of the circle is shown here with a point on the Earth that is not the Earth’s center but just right to its center. Figure b shows the Sun and the counterclockwise rotation of the Earth around it, in an elliptical path, which has wiggles. Along this path the center of mass of the Earth-Moon is also shown; it follows non-wiggled elliptical path.
Figure 5.11: (a) Earth and the Moon rotate approximately once a month around their common center of mass. (b) Their center of mass orbits the Sun in an elliptical orbit, but Earth’s path around the Sun has “wiggles” in it. Similar wiggles in the paths of stars have been observed and are considered direct evidence of planets orbiting those stars. This is important because the planets’ reflected light is often too dim to be observed.

Tides: Evidence of the Moon’s Gravitational Pull

One of the most visible consequences of the Moon’s gravity is tides on Earth’s oceans. Because water is mobile, the Moon’s gravity pulls more strongly on the side of Earth closest to it, creating a high tide. A second high tide occurs on the far side, where Earth is pulled away from the water (Figure 5.12).

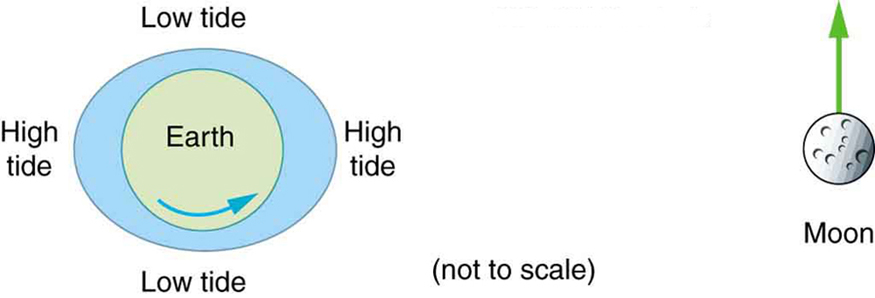
The given figure shows an ellipse, inside which there is a circular image of the Earth. There is a curved arrow in the lower part of the Earth’s image pointing in the counterclockwise direction. The right and left side of the ellipse are labeled as High tide and the top and bottom side are labeled as Low tide. Alongside this image a circular image of the Moon is also given with dots showing the crates over it. A vertically upwards vector from its top is also shown, which indicates the direction of the Moon’s velocity.
Figure 5.12: The Moon causes ocean tides by attracting the water on the near side more than Earth, and by attracting Earth more than the water on the far side. The distances and sizes are not to scale. For this simplified representation of the Earth-Moon system, there are two high and two low tides per day at any location, because Earth rotates under the tidal bulge.

As Earth rotates under these tidal bulges, most coastal locations experience two high tides and two low tides every 24 hours and 50.4 minutes, aligning with the Moon’s orbital motion.

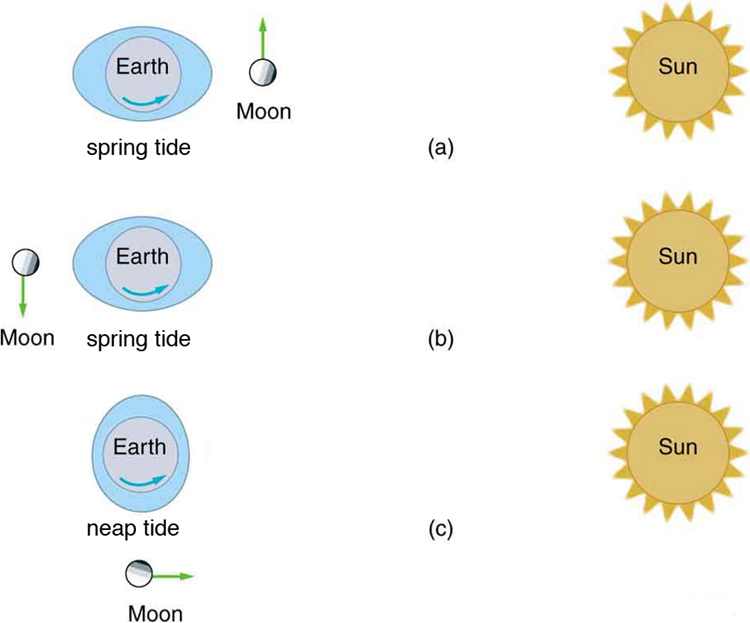
The Sun also contributes to tides, but its influence is only about half that of the Moon. When the Sun, Earth, and Moon align (new or full moon), their gravitational effects reinforce one another, creating spring tides, the highest tides. When they form a right angle (first or third quarter), the effects partially cancel, causing neap tides, the smallest tides (Figure 5.13).

Figure a shows an ellipse, inside which there is a circular image of the Earth. There is a curved arrow in the lower part of the Earth’s image pointing in the counterclockwise direction. Alongside this image a circular image of the Moon is also given with dots showing the crates over it. A vertically upward vector from its top is also drawn, which shows the direction of velocity. To the right side of the image, an image of the Sun is also shown, in a circular shape with pointed wiggles throughout its boundary. Figure b shows an ellipse, inside which there is a circular image of the Earth. There is a curved arrow in the lower part of the Earth’s image pointing in the counterclockwise direction. Alongside this image a circular image of the Moon is also given with dots showing the crates over it. A vertical downward vector from its bottom is also drawn, which shows the direction of velocity. To the right side of the image, an image of the Sun is also shown, in a circular shape and pointed wiggles throughout its boundary. Figure c shows an ellipse, inside which there is a circular image of the Earth. There is a curved arrow in the lower part of the Earth’s image pointing in the counterclockwise direction. Alongside this image a circular image of the Moon is also given with dots showing the crates over it. A horizontal rightward vector from its right side is also drawn, which shows the direction of velocity. To the right side of the image, an image of the Sun is also shown, in a circular shape and pointed wiggles throughout its boundary.
Figure 5.13: (a, b) Spring tides: The highest tides occur when Earth, the Moon, and the Sun are aligned. (c) Neap tide: The lowest tides occur when the Sun lies at [latex]\text{90º}[/latex] to the Earth-Moon alignment. Note that this figure is not drawn to scale.

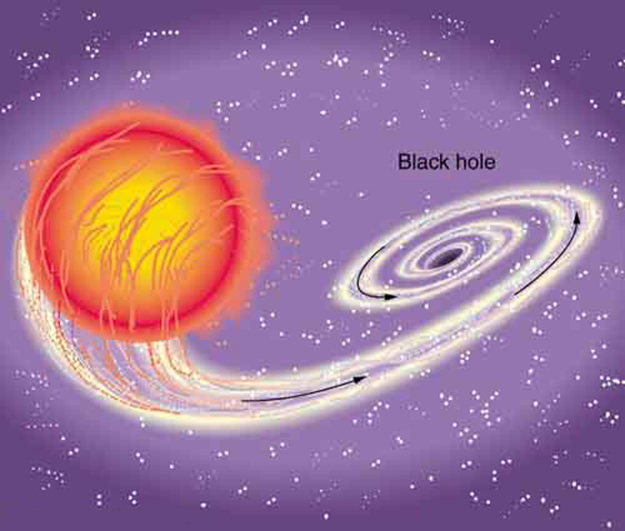
Tidal effects also occur in extreme conditions—near black holes, for instance. These objects generate such intense tidal forces that they can tear matter from nearby stars, forming luminous accretion disks (Figure 5.14).

The figure shows a star in sky near a black hole. The tidal force of the black hole is tearing the matter from the star’s surface.
Figure 5.14: A black hole is an object with such strong gravity that not even light can escape it. This black hole was created by the supernova of one star in a two-star system. The tidal forces created by the black hole are so great that it tears matter from the companion star. This matter is compressed and heated as it is sucked into the black hole, creating light and X-rays observable from Earth.

“Weightlessness” and Microgravity in Orbit

Astronauts in orbit appear weightless, but gravity is still acting on them. They are in free fall, continuously falling toward Earth but traveling forward fast enough to remain in orbit. This state is known as apparent weightlessness, illustrated by astronauts aboard the International Space Station (Figure 5.15).

In such environments, microgravity—very small net acceleration—is experienced. This has significant biological and technological implications:

  • Muscle atrophy and bone density loss are common in astronauts.

  • Cardiovascular adaptations occur due to loss of pressure gradients.

  • The immune system weakens, increasing infection risk.

  • Some bacteria grow faster in space, while others produce more antibiotics.

  • High-quality crystal growth in microgravity enables advanced materials research.

Plants, which rely on gravity to orient their roots and shoots, may play vital roles in life support systems during long-term space missions. However, more research is needed on how microgravity affects their development.

 

The figure shows some astronauts floating inside the International Space Station
Figure 5.15: Astronauts experiencing weightlessness on board the International Space Station. (credit: NASA)

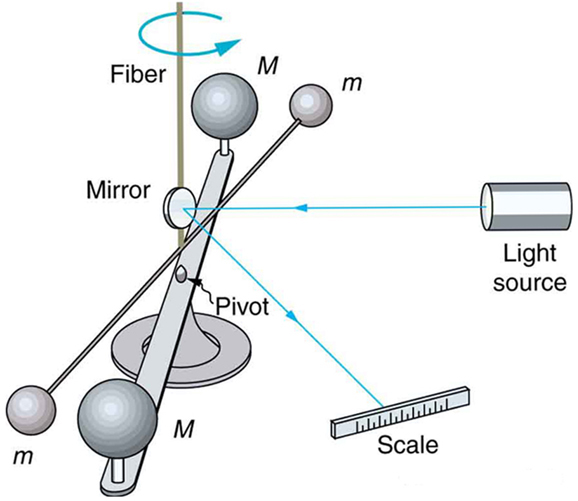
The Cavendish Experiment: Measuring [latex]G[/latex]

The gravitational constant [latex]G[/latex] was first measured by Henry Cavendish in 1798 using a torsion balance apparatus (Figure 5.16). This device measured the tiny attraction between lead spheres, allowing Cavendish to calculate the strength of gravity between known masses.

Using Newton’s law:

[latex]F = G \frac{mM}{r^2}[/latex]

and substituting [latex]F = mg[/latex] (the object’s weight), we get:

[latex]mg = G \frac{mM}{r^2}[/latex]

Canceling [latex]m[/latex]:

[latex]g = G \frac{M}{r^2}[/latex]

Solving for Earth’s mass:

[latex]M = \frac{gr^2}{G}[/latex]

With accurate values for [latex]g[/latex], [latex]r[/latex] (Earth’s radius), and [latex]G[/latex], we can compute Earth’s mass. This was one of the first scientific estimates of a planet’s mass.

In the figure, there is a circular stand at the floor holding two weight bars over it attached through an inverted cup shape object fitted over the stand. The first bar over this is a horizontal flat panel and contains two spheres of mass M at its end. Just over this bar is a stick shaped bar holding two spherical objects of mass m at its end. Over to this bar is mirror at the center of the device facing east. The rotation of this device over the axis of the stand is anti-clockwise. A light source on the right side of the device emits a ray of light toward the mirror which is then reflected toward a scale bar which is on the right to the device below the light source.
Figure 5.16: Cavendish used an apparatus like this to measure the gravitational attraction between the two suspended spheres ([latex]m[/latex]) and the two on the stand ([latex]M[/latex]) by observing the amount of torsion (twisting) created in the fiber. Distance between the masses can be varied to check the dependence of the force on distance. Modern experiments of this type continue to explore gravity.

Modern Advances in Gravitational Experiments

Experiments following Cavendish’s method have refined our understanding of gravity:

  • Eötvös-type experiments confirmed that gravity acts equally on all substances, supporting the equivalence principle.

  • Modern torsion balances test gravity’s behavior at millimeter scales, searching for deviations from the inverse-square law.

  • These tests also probe for a fifth force or signs of quantum gravity.

  • Recent studies confirm that gravitational energy contributes to mass, in line with general relativity.

These continued efforts help us verify and extend Newton’s ideas, bridging toward modern theories of gravity.

Gravitational Orbits: A Universal Phenomenon

From the Moon’s orbit around Earth to artificial satellites and distant star systems, gravitationally bound orbits are everywhere. These orbits include:

  • Earth’s natural and artificial satellites

  • Planetary orbits around the Sun

  • Binary star systems

  • Galaxy clusters held together by mutual gravitational attraction

Although real-world gravitational systems can be complex and require numerical computation, many important insights come from examining simplified orbital models governed purely by Newtonian gravity.

    Simplifying Assumptions for Orbital Motion

    To explore orbital motion analytically, we consider a special but very common case:

    • A small mass [latex]m[/latex] (e.g., a satellite or planet) orbits a much larger mass [latex]M[/latex] (e.g., a planet or star).

    • The gravitational interaction dominates, and outside influences from other bodies are negligible.

    • The center of mass lies within [latex]M[/latex], allowing us to approximate it as stationary.

    This idealization applies to:

    • The Moon orbiting Earth

    • Earth and other planets orbiting the Sun

    • Moons of Jupiter, Saturn, and other planets

    • Artificial satellites orbiting Earth

    These assumptions provide the foundation for understanding Kepler’s laws of planetary motion.

    Kepler’s Laws of Planetary Motion

    Developed by Johannes Kepler in the early 1600s, these laws describe planetary orbits based on the extensive astronomical data collected by Tycho Brahe. Though originally formulated to describe planets orbiting the Sun, Kepler’s laws apply to any object in gravitational orbit under the conditions noted above.

    Kepler’s First Law: Elliptical Orbits

    The orbit of each planet is an ellipse, with the Sun at one focus.

    An ellipse is a closed, elongated curve defined by two fixed points called foci. The sum of the distances from any point on the ellipse to each focus is constant (Figure 5.17a). A circle is a special case of an ellipse in which both foci coincide.

    For any gravitationally bound object orbiting another, the path is elliptical, with the more massive body (e.g., the Sun or a planet) located at one focus (Figure 5.17b).

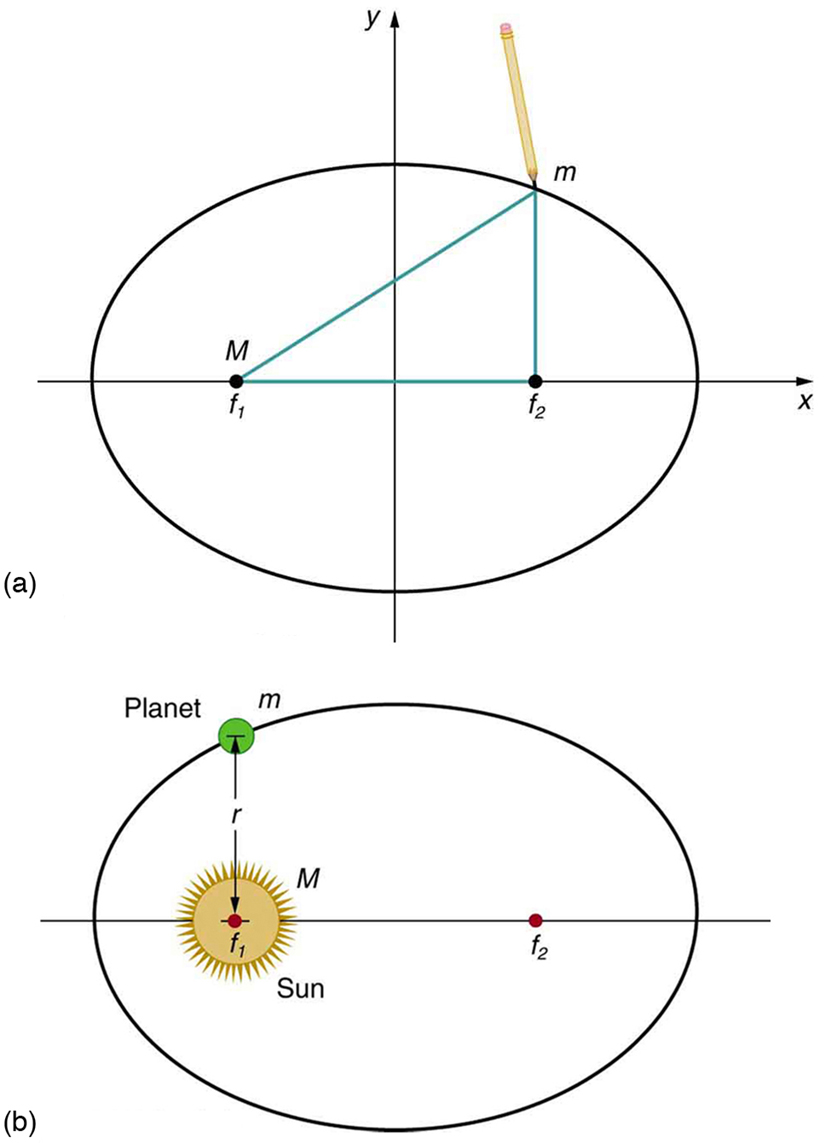
    In figure a, an ellipse is shown on the coordinate axes. Two foci of the ellipse are joined to a point m on the ellipse. A pencil is shown at the point m. In figure b the elliptical path of a planet is shown. At the left focus f-one of the path the Sun is shown. The planet is shown just above the Sun on the elliptical path.
    Figure 5.17: (a) An ellipse traced with two foci shows the geometric definition.
    (b) In a gravitational orbit, the smaller body [latex]m[/latex] moves around the larger mass [latex]M[/latex] along an elliptical path with [latex]M[/latex] at one focus.

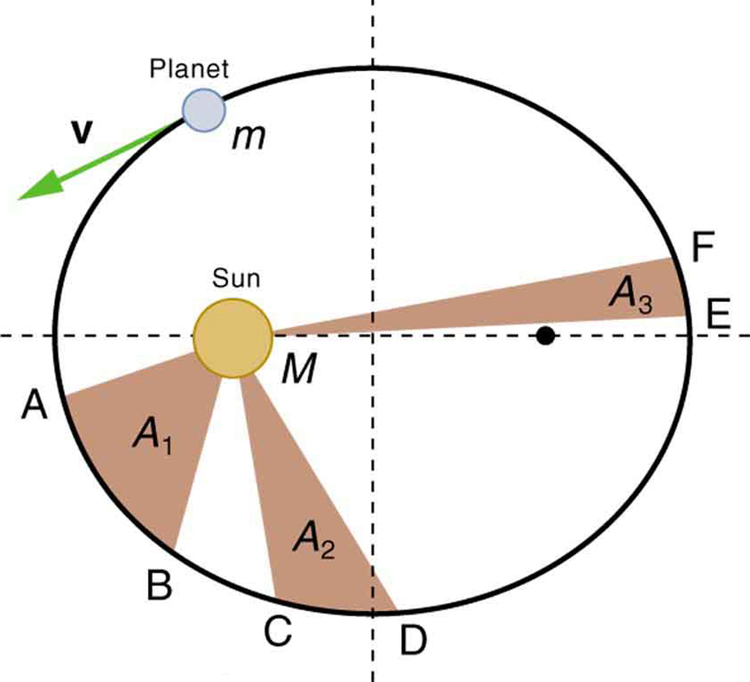
    Kepler’s Second Law: Equal Areas in Equal Times

    A line drawn from the orbiting object to the central body sweeps out equal areas in equal intervals of time.

    This law implies that the object moves faster when it is closer to the central mass and slower when it is farther away (Figure 5.18). The varying speed maintains the constant areal rate of motion, a consequence of conservation of angular momentum.

    In the figure, the elliptical path of a planet is shown. The Sun is at the left focus. Three shaded regions M A B, M C D and M E F are marked on the figure by joining the Sun to the three pairs of points A B, C D, and E F on the elliptical path. The velocity of the planet is shown on the planet in a direction tangential to the path.
    Figure 5.18: Equal area segments (A–B, C–D, E–F) are swept in equal time intervals. The planet moves faster near perihelion (closest point) and slower near aphelion (farthest point).

    Kepler’s Third Law: Harmonic Law

    The square of the orbital period of a planet is proportional to the cube of the average orbital radius.

    Mathematically:

    [latex]\frac{T_1^2}{T_2^2} = \frac{r_1^3}{r_2^3}[/latex]

    Here:

    • [latex]T_1[/latex] and [latex]T_2[/latex] are the orbital periods of two planets, and

    • [latex]r_1[/latex] and [latex]r_2[/latex] are their respective average orbital radii.

    This relation applies only when both small masses orbit the same large central mass. The law is empirical—it describes the motion but does not explain the underlying cause. The physical origin (gravitational force) was later provided by Newton.

    💡 Note: While Kepler formulated his laws for planets orbiting the Sun, these laws apply more generally to any gravitational two-body system where a small mass orbits a much larger one.

    Example 5.5: Find the Time for One Orbit of an Earth Satellite

    Given that the Moon orbits Earth each 27.3 d and that it is an average distance of [latex]3.84×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] from the center of Earth, calculate the period of an artificial satellite orbiting at an average altitude of 1500 km above Earth’s surface.

    Strategy

    The period, or time for one orbit, is related to the radius of the orbit by Kepler’s third law, given in mathematical form in [latex]\frac{{T}_{1}^{ 2}}{{T}_{2}^{ 2}}=\frac{{r}_{1}^{ 3}}{{r}_{2}^{ 3}}[/latex]. Let us use the subscript 1 for the Moon and the subscript 2 for the satellite. We are asked to find [latex]{T}_{2}[/latex]. The given information tells us that the orbital radius of the Moon is [latex]{r}_{1}=3\text{.}\text{84}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex], and that the period of the Moon is [latex]{T}_{1}=\text{27.3 d}[/latex]. The height of the artificial satellite above Earth’s surface is given, and so we must add the radius of Earth (6380 km) to get [latex]{r}_{2}=\left(\text{1500}+\text{6380}\right)\phantom{\rule{0.25em}{0ex}}\text{km}=\text{7880}\phantom{\rule{0.25em}{0ex}}\text{km}[/latex]. Now all quantities are known, and so [latex]{T}_{2}[/latex] can be found.

    Solution

    Kepler’s third law is

    [latex]\frac{{T}_{1}^{ 2}}{{T}_{2}^{ 2}}=\frac{{r}_{1}^{ 3}}{{r}_{2}^{ 3}}\text{.}[/latex]

    To solve for [latex]{T}_{2}[/latex], we cross-multiply and take the square root, yielding

    [latex]{T}_{2}^{ 2}={T}_{1}^{ 2}{\left(\frac{{r}_{2}}{{r}_{1}}\right)}^{3}[/latex]
    [latex]{T}_{2}={T}_{1}{\left(\frac{{r}_{2}}{{r}_{1}}\right)}^{3/2}\text{.}[/latex]

    Substituting known values yields

    [latex]\begin{array}{lll}{T}_{2}& =& \text{27.3 d}×\frac{\text{24.0 h}}{\text{d}}×{\left(\frac{\text{7880 km}}{3.84×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{km}}\right)}^{3/2}\\ & =& \text{1.93 h.}\end{array}[/latex]

    Discussion

    This is a reasonable period for a satellite in a fairly low orbit. It is interesting that any satellite at this altitude will orbit in the same amount of time. This fact is related to the condition that the satellite’s mass is small compared with that of Earth.

    Newton’s Laws Lead to Kepler’s Third Law

    Let us derive Kepler’s third law using Newton’s law of gravitation and Newton’s second law. Consider a satellite of mass [latex]m[/latex] orbiting a much larger central mass [latex]M[/latex] (e.g., a planet orbiting the Sun). We assume a circular orbit for simplicity. Gravity provides the centripetal force that keeps the satellite in orbit:

    [latex]F_{\text{net}} = ma_{\text{c}} = m \frac{v^2}{r}[/latex]

    Now, applying Newton’s law of universal gravitation as the source of this centripetal force:

    [latex]F_{\text{gravity}} = G \frac{mM}{r^2}[/latex]

    Equating the two forces:

    [latex]G \frac{mM}{r^2} = m \frac{v^2}{r}[/latex]

    Canceling [latex]m[/latex] from both sides and solving for [latex]v^2[/latex]:

    [latex]G \frac{M}{r} = v^2[/latex]

    Since the orbital speed [latex]v[/latex] is related to the period [latex]T[/latex] of revolution by the circumference of the orbit:

    [latex]v = \frac{2\pi r}{T}[/latex]

    Substitute this into the expression for [latex]v^2[/latex]:

    [latex]G \frac{M}{r} = \left(\frac{2\pi r}{T}\right)^2 = \frac{4\pi^2 r^2}{T^2}[/latex]

    Solving for [latex]T^2[/latex]:

    [latex]T^2 = \frac{4\pi^2}{GM} r^3[/latex]

    This shows that for any object orbiting the same central mass [latex]M[/latex], the square of the orbital period is proportional to the cube of the orbital radius:

    [latex]\frac{T_1^2}{T_2^2} = \frac{r_1^3}{r_2^3}[/latex]

    This is Kepler’s third law. It applies to all satellites orbiting the same parent body.

    Using Kepler’s Third Law to Determine Mass

    Rewriting the result:

    [latex]\frac{r^3}{T^2} = \frac{GM}{4\pi^2}[/latex]

    This formula allows us to determine the mass [latex]M[/latex] of the central body if we know the satellite’s orbital radius and period. This method has been extensively used to calculate the masses of stars, planets, and galaxies.

    Table of Orbital Data and [latex]r^3 / T^2[/latex] Ratios

    The table below shows orbital data for various bodies orbiting the Sun and Jupiter. The values of [latex]r^3 / T^2[/latex] remain constant (to within measurement uncertainty), confirming the predictive power of Kepler’s third law and Newtonian gravity.

    Table 5.3: Orbital Data and Kepler’s Third Law
    Parent Satellite Average orbital radius r(km) Period T(y) r3 / T2 (km3 / y2)
    Earth Moon [latex]3.84×{\text{10}}^{5}[/latex] 0.07481 [latex]1\text{.}\text{01}×{\text{10}}^{\text{19}}[/latex]
    Sun Mercury [latex]5\text{.}\text{79}×{\text{10}}^{7}[/latex] 0.2409 [latex]3\text{.}\text{34}×{\text{10}}^{\text{24}}[/latex]
    Venus [latex]1\text{.}\text{082}×{\text{10}}^{8}[/latex] 0.6150 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Earth [latex]1\text{.}\text{496}×{\text{10}}^{8}[/latex] 1.000 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Mars [latex]2\text{.}\text{279}×{\text{10}}^{8}[/latex] 1.881 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Jupiter [latex]7\text{.}\text{783}×{\text{10}}^{8}[/latex] 11.86 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Saturn [latex]1\text{.}\text{427}×{\text{10}}^{9}[/latex] 29.46 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Neptune [latex]4\text{.}\text{497}×{\text{10}}^{9}[/latex] 164.8 [latex]3\text{.}\text{35}×{\text{10}}^{\text{24}}[/latex]
    Pluto [latex]5\text{.}\text{90}×{\text{10}}^{9}[/latex] 248.3 [latex]3\text{.}\text{33}×{\text{10}}^{\text{24}}[/latex]
    Jupiter Io [latex]4\text{.}\text{22}×{\text{10}}^{5}[/latex] 0.00485 (1.77 d) [latex]3\text{.}\text{19}×{\text{10}}^{\text{21}}[/latex]
    Europa [latex]6\text{.}\text{71}×{\text{10}}^{5}[/latex] 0.00972 (3.55 d) [latex]3\text{.}\text{20}×{\text{10}}^{\text{21}}[/latex]
    Ganymede [latex]1\text{.}\text{07}×{\text{10}}^{6}[/latex] 0.0196 (7.16 d) [latex]3\text{.}\text{19}×{\text{10}}^{\text{21}}[/latex]
    Callisto [latex]1\text{.}\text{88}×{\text{10}}^{6}[/latex] 0.0457 (16.19 d) [latex]3\text{.}\text{20}×{\text{10}}^{\text{21}}[/latex]

    Small deviations arise due to:

    • Uncertainties in measurement

    • Gravitational perturbations by other bodies

    Such perturbations have even led to the discovery of new planets and moons, a triumph of Newtonian gravity.

    Simplicity and the Power of Universal Laws

    Kepler’s laws describe planetary motion, but Newton’s gravitational theory explains them. This marked a shift in science—from description to causation through universal laws.

    “Truth is ever to be found in simplicity.” — Isaac Newton

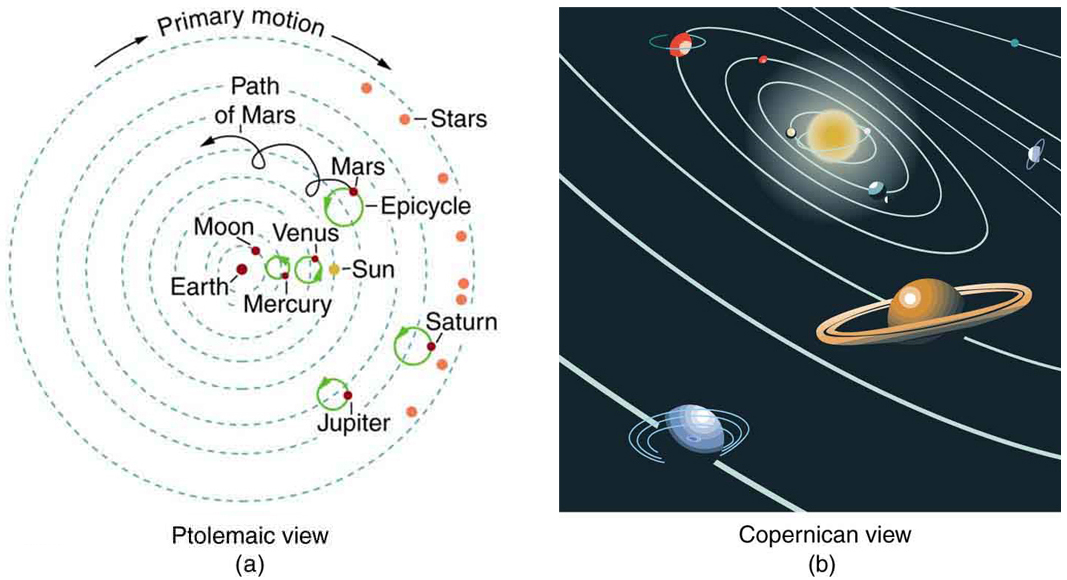
    The Copernican model (Figure 5.19(b)) exemplifies this simplicity, explaining planetary motion using a few core principles. By contrast, the Ptolemaic model (Figure 5.19(a)) relied on complex geometrical constructions without causal explanation.

    In figure a the paths of the different planets are shown in the forms of dotted concentric circles with the Earth at the center with its Moon. The Sun is also shown revolving around the Earth. Each planet is labeled with its name. On the planets Mercury, Venus, Mars, Jupiter and Saturn green colored epicycles are shown. In the figure b Copernican view of planet is shown. The Sun is shown at the center of the solar system. The planets are shown moving around the Sun.
    Figure 5.19:(a) Ptolemaic model: Earth at the center; planets and stars revolve in complex, nested circular paths. (b) Copernican-Newtonian model: The Sun at the center, governed by universal laws of motion and gravity.

    Section Summary

    • An object in free fall experiences constant acceleration if air resistance is negligible.

    • On Earth, all free-falling objects accelerate downward due to gravity, with acceleration [latex]g[/latex] averaging

      [latex]g = 9.80\ \text{m/s}^2.[/latex]

    • The sign of the acceleration [latex]a[/latex] depends on the choice of coordinate system:

      • If upward is chosen as positive, then

        [latex]a = -g = -9.80\ \text{m/s}^2[/latex] (acceleration is negative)

      • If downward is chosen as positive, then

        [latex]a = +g = 9.80\ \text{m/s}^2[/latex] (acceleration is positive)

    • Since acceleration is constant, the kinematic equations can be applied by substituting either [latex]+g[/latex] or [latex]-g[/latex] for [latex]a[/latex] as appropriate.

    • For free-falling objects, up is normally taken as positive for displacement, velocity, and acceleration.

    • Newton’s Universal Law of Gravitation states that:

      Every mass attracts every other mass through a force proportional to the product of their masses and inversely proportional to the square of the distance between them.

      Mathematically:

      [latex]F = G \frac{mM}{r^2}[/latex]

      • [latex]F[/latex] is the gravitational force,

      • [latex]G = 6.674 \times 10^{-11} , \text{N} \cdot \text{m}^2/\text{kg}^2[/latex],

      • [latex]m[/latex] and [latex]M[/latex] are the masses involved,

      • [latex]r[/latex] is the distance between their centers of mass.

      This law applies universally—from falling apples to orbiting galaxies—and continues to be confirmed by experiments and observations.

    • Kepler’s third law states that [latex]T^2 \propto r^3[/latex] for orbiting bodies.

    • It can be derived from Newton’s second law and his law of gravitation.

    • The resulting formula [latex]T^2 = \frac{4\pi^2}{GM} r^3[/latex] connects orbit period to central mass and radius.

    • These ideas highlight the unity and simplicity of physics, showing how one fundamental force explains a wide variety of natural phenomena.

    Glossary

    free-fall
    the state of movement that results from gravitational force only
    acceleration due to gravity
    acceleration of an object as a result of gravity
    definition

    License

    Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

    Gravity and falling objects Copyright © by Esperanza Zenon; James Boffenmyer; Mostafa Elaasar; and Shirley Vides is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

    Share This Book